La entrada de hoy de la sección Matemoción del Cuaderno de Cultura Científica la vamos a dedicar a un sencillo resultado que se obtiene aplicando el conocido teorema de Pitágoras, pero que tiene un nombre sugerente, el teorema de la bandera británica. Aunque como se menciona en el título de esta entrada, bien podría llamarse teorema de la ikurriña, por el diseño de esta bandera.

El teorema de la bandera británica es un resultado de la geometría euclidiana plana que dice lo siguiente:

Si ABCD es un rectángulo y P un punto dentro del mismo (o fuera), entonces la suma de las distancias al cuadrado de P a dos vértices opuestos del rectángulo es igual a la misma suma a los otros dos vértices opuestos. Es decir,

PA² + PC² = PB² + PD².

Podemos interpretar el teorema de la bandera británica en función de áreas de cuadrados construidos a partir de los vértices A, B, C, D y del punto P. En concreto, los cuadrados rojos de la siguiente imagen (cuyos lados son PA y PC) tienen la misma área en conjunto, que los cuadrados verdes (cuyos lados son PB y PD).

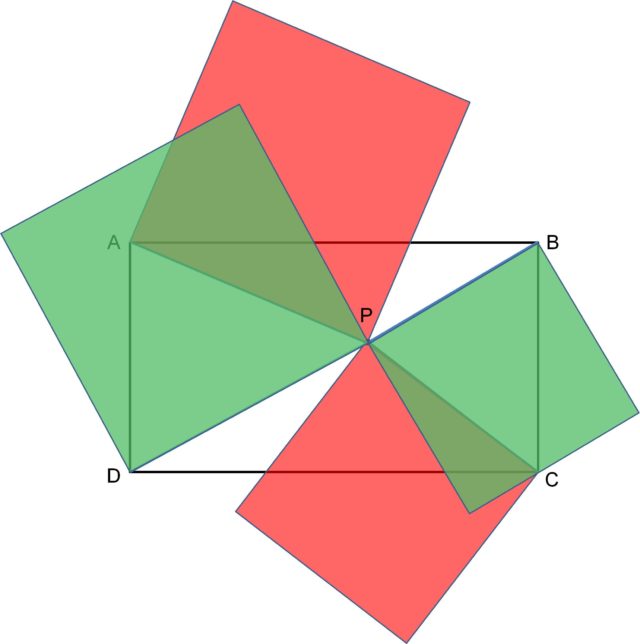
Este resultado de la geometría euclidiana aparece en la edición de 1848 de Los Elementos de Euclides realizada por el científico irlandés Dionysius Lardner (1793-1859), quien fue un gran divulgador de la ciencia y la tecnología, conocido además por ser el editor de la enciclopedia, de 133 volúmenes, Cabinet Cyclopedia (1830-1844). En esta edición de Los Elementos se añadían ejercicios de geometría, entre los que está, en la página 87 y numerado como el resultado (306), el hoy conocido como teorema de la bandera británica.

De hecho, cuando termina el contenido del Libro II de los Elementos, Dionysius Lardner escribe “The following is a selection from some of the most useful and remarkable theorems and problems, which may be inferred from the second book”, es decir, “Lo siguiente es una selección de algunos de los teoremas y problemas más útiles y notables, que se pueden obtener a partir de los resultados del libro segundo”. Y entre los resultados del libro segundo de Los Elementos de Euclides está el teorema de Pitágoras, que es el que se utiliza precisamente para demostrar el teorema de la bandera británica.

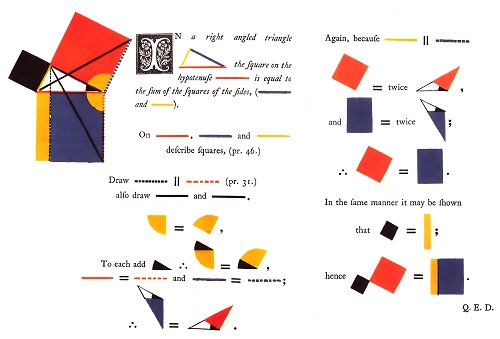
Aunque es muy conocido, recordemos que el teorema de Pitágoras nos dice que dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos (la famosa expresión a²+b²=c², si a y b son los catetos y c la hipotenusa).

A continuación, veamos la sencilla demostración del teorema de la bandera británica. Dado el rectángulo A, B, C, D, como el de la imagen anterior, y el punto interior P (un argumento similar se realizaría para el caso de ser P exterior), trazamos por el punto P una línea vertical y otra horizontal que determina cuatro puntos X, Y, Z, T al intersecar los lados del rectángulo.

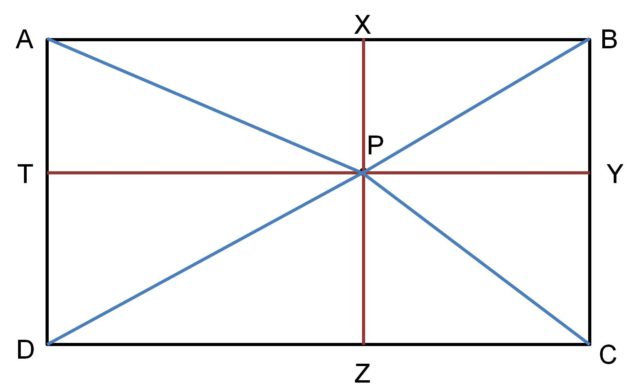
Como en el teorema que estamos demostrando nos interesan los segmentos PA, PB, PC y PD, que son las hipotenusas de los triángulos rectángulos AXP, BYP, CZP y DTP (como vemos en la imagen anterior), entonces podemos aplicar el teorema de Pitágoras sobre estos triángulos rectángulos, obteniendo que:

PA² = AX² + XP² = AX² + AT², PC² = CZ² + ZP² = CZ² + CY²,

PB² = BY² + YP² = BY² + BX², PD² = DT² + TP² = DT² + DZ².

Y ahora, es evidente que:

PA² + PC² = (AX² + AT²) + (CZ² + CY²) =

(AX² + CY²) + (AT² + CZ²) =

(DZ² + DT²) + (BY² + BX²) = PD² + PB².

Como observamos, el teorema de la bandera británica es una consecuencia inmediata del teorema de Pitágoras, que bien puede ser un sencillo problema para aquellas personas que están aprendiendo geometría plana, y en particular, el teorema de Pitágoras.

El nombre de teorema de la bandera británica se debe a que el esquema anterior utilizado en la demostración recuerda, en alguna medida, a la bandera británica.

El título de esta entrada, el teorema de la ikurriña, se debe a que de igual forma, el esquema de la demostración del resultado anterior nos recuerda al diseño de la ikurriña, en particular, al diseño original de los hermanos Arana, los fundadores del Partido Nacionalista Vasco (1894), los políticos Luis y Sabino Arana.

El teorema de la bandera británica se puede generalizar en varios sentidos, uno de ellos es el siguiente. Dado un paralelogramo ABCD, no necesariamente un rectángulo, y un punto P, entonces en general no es cierto que la suma de las distancias al cuadrado de P a dos vértices opuestos del rectángulo sea igual a la misma suma a los otros dos vértices opuestos, PA² + PC² = PB² + PD², sin embargo, la diferencia entre ambas sumas (PA² + PC²) – (PB² + PD²) es constante para cada paralelogramo, es decir, depende de la forma del paralelogramo, pero no de la posición del punto P.

Bibliografía

1.- Dionysius Lardner, The First Six Books of the Elements of Euclid, H. G. Bohn, 1848.

2.- Oliver Byrne, The First Six Books of the Elements of Euclid (edición de 1847), facsímil publicado por Taschen, 2010.

3.- British Flag Theorem (Wikipedia).

4.- Jacques Hadamard, Lessons in Geometry: Plane Geometry, AMS, 2008.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica