La pesadilla de las matemáticas

Tengo una pesadilla recurrente. Me suele asaltar más o menos una vez al mes, y me hace pasarlo realmente mal. El argumento es siempre el mismo: recibo una carta en la que se me comunica que tengo que regresar al instituto, concretamente a 3º de la E.S.O. ¿El motivo?: alguien ha descubierto que suspendí las matemáticas cuando tenía quince años. Poco después me veo en mi pupitre, rodeado de estudiantes adolescentes, y mi única preocupación es saber si me dejarán hacer el examen final e irme o si tendré que asistir al curso completo. Nunca llego a preguntarlo, siempre me despierto antes, sudando y con una angustia horrible.

Lo más aterrador de este sueño es que, en efecto, suspendí las matemáticas en el curso 1998/1999. No solamente las suspendí, sino que también las odié. Quizá estén ustedes esperando que culpe a un mal profesor, o a algún problema de la adolescencia… pero lamento decepcionarles: la culpa fue mía y solo mía. Simplemente, las matemáticas no se me daban nada bien; mis profesores hicieron todo lo que pudieron.

Lo curioso del caso es que tan solo tres años después ingresé como estudiante en la facultad de física de la Universidad Complutense de Madrid, donde, para mayor misterio, me especialicé en física matemática. Para acabar de rizar el rizo, hoy estoy doctorándome en matemática aplicada.

¿Qué pasó entre medias? Esta es la pregunta que intentaré responder en las próximas líneas.

¿Se siente identificado?

Si usted, querido lector, ha odiado las matemáticas en algún momento de su vida, o incluso durante toda ella, no puedo hacer menos que darle la bienvenida al club. Lamentablemente no se trata de un club demasiado exclusivo… ¡tenemos cientos de millones de miembros!

Las matemáticas son complicadas de estudiar. Hacerlo de forma memorística, estrategia que suele dar resultado con la mayoría de asignaturas, no vale para gran cosa en el caso de las matemáticas. Y lo que es peor, dado que la mayoría de sus resultados no son opinables, los errores, de haberlos, son evidentes e indiscutibles. Es imposible tener un ejercicio de matemáticas casi bien: o está bien, o no lo está.

Las matemáticas son bonitas… o eso aseguran los que las conocen. Sin embargo, ¿qué hay de bonito en los centenares de ejercicios de factorización de polinomios que tanto tiempo nos consumieron en los años de instituto?

Pues bien, tengo que darle la razón. Factorizar, reducir fracciones, calcular derivadas, … todo eso es aburrido. Pero he aquí algo que quizá le sorprenda: todos esos tediosos cálculos no son más que una pequeña, pequeñísima parte de las matemáticas. Por desgracia, la parte del principio. La cosa se pone interesante más adelante.

Entonces, ¿de qué van las matemáticas?

Al contrario de lo que mucha gente cree, las matemáticas no tratan (solamente) de números. Me gusta definir las matemáticas como el brazo armado de la lógica. Vamos, que las matemáticas van de pensar, de sacar conclusiones a partir de unas premisas dadas. ¿Hay alguien en la sala que no haga esto varias veces al día?

Visto así, no es extraño que encuentren aplicaciones por doquier: allí donde pueda utilizarse el pensamiento lógico para arrojar algo de luz, las matemáticas tendrán cabida. Sus aplicaciones son innumerables. Desde los desafortunadísimos ejemplos cotidianos tipo “para que no te timen con la cuenta en el bar”, hasta sus usos en todas y cada una de las ramas de la ciencia y la tecnología. Pasando, por supuesto, por aplicaciones peculiares, como su uso en dinámica de creencias conspiranoicas o para llenar más rápido un avión de pasajeros… que a estas alturas ya no deberían sorprendernos.

Bueno, ¿qué pasó en el instituto?

Para los más cotillas, dejo aquí la narración de mi experiencia. Como todas, es personal e intransferible, pero es la única que tengo.

Pasé los tres últimos años de instituto lidiando penosamente con las matemáticas y aprobándolas a trompicones. Necesité de la paciente ayuda de un profesor particular durante todo aquel tiempo, e incluso para preparar el examen de acceso a la universidad (cuya prueba de matemáticas suspendí con un 4.5).

Curiosamente, la física se me daba bien… y ahora entiendo por qué. Mi problema no estaba en el razonamiento lógico, sino únicamente en la aritmética. Entonces yo era incapaz de llevar a cabo una operación larga sin cometer errores que diesen al traste con todo el problema. En la clase de matemáticas, al tratarse de problemas (aparentemente) abstractos, carecía de herramientas para saber si me había equivocado o no. Sin embargo, en clase de física, los problemas eran de todo menos abstractos. Si tras hacer los cálculos el coche del problema se movía a veinte mil kilómetros por hora, o la masa de Alicia era de quince toneladas… bastaba volver atrás y encontrar el error de cálculo.

Resumiendo: en los problemas de física podía utilizar mi intuición con más o menos acierto, pero la mayoría de problemas matemáticos, al estar propuestos en abstracto, se convertían en procesos mecánicos en los que no me quedaba más remedio que poner el piloto automático e ir a ciegas. Tuve pues que entrenar mis habilidades de cálculo. Fue un proceso lento, en el cual la física, con su evidente atractivo y utilidad, me ayudó a mantenerme motivado.

Comparto aquí uno de los trucos que utilicé entonces para no meter la pata en los cálculos. Es muy simplón, pero para mí fue de gran ayuda: consiste en dar un paso atrás, y luego dos adelante (ver figura).

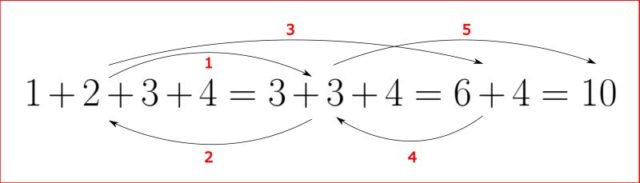
De modo que cada vez que avancemos en un desarrollo, volveremos un paso atrás para comprobar que todo es correcto, y solo entonces daremos dos pasos adelante para continuar con el ejercicio. Parece (y es) una chorrada, pero reduce mucho la probabilidad de cometer errores tontos.

¿Por qué no lo hacemos mejor?

Naturalmente, también se puede educar la intuición matemática. Muchos profesores hacen una grandísima labor en este sentido. Sin embargo, la mayor parte del peso de la educación matemática preuniversitaria se la llevan los cálculos rutinarios y el “hacer mano”. Para bien o para mal, esto es necesario, pues esta habilidad es realmente una herramienta básica. Sin embargo, aunque reconozco abiertamente que no se me ocurre idea alguna para hacerlo mejor, me da en la nariz que no le estamos dando el peso suficiente a las ideas detrás de los cálculos. A título de ejemplo, considere el lector cuál de estas dos preguntas tiene más probabilidades de ser respondida correctamente por un estudiante de, pongamos, 2º de bachillerato:

1. ¿Cuál es la derivada de f(x) = x²?
2. ¿Qué es una derivada?

No puedo dejar de preguntarme cuántas personas con genuino talento matemático habrán tirado la toalla abrumadas por este primer encontronazo con la parte más tediosa y frustrante de las matemáticas.

Un libro

El giro decisivo en mi relación con las matemáticas llegó por casualidad, en una librería. Necesitaba un libro de texto para preparar mi curso de Cálculo I, una asignatura de primero de carrera. La librería, que no andaba muy bien surtida en cuanto a libros científicos, solamente disponía de un título: Cálculo y Geometría Analítica, de George F. Simmons. Tras una ojeada, que a día de hoy se me antoja vergonzosamente breve y desganada, compré aquel libro. Aún tardé un par de semanas en darme cuenta del tesoro que me había llevado a casa.

Se trata de un curso completo de cálculo infinitesimal, con una peculiaridad interesante, común a todos los libros del mismo autor: está repleto de información sobre aplicaciones, historia de las matemáticas, biografías de matemáticos históricos y discusiones sobre los problemas que les llevaron a la fama. Esto lo convierte en un libro voluminoso, largo, pero también muy placentero de leer. Cada lección aporta no uno, sino varios contextos (el histórico, el aplicado, el humano), lo cual permite “agarrar los conceptos por varios sitios a la vez”. En resumen: convertirlos en algo intuitivo.

Y es que las matemáticas, como toda actividad humana, están llenas de historias con planteamiento, nudo y desenlace*.

* para el lector interesado, recomiendo encarecidamente otro libro del mismo autor: Calculus Gems: Brief Lives and Memorable Mathematics

Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.