En la entrada Los números enamorados del Cuaderno de Cultura Científica, habíamos presentado algunas familias de números naturales que deben su propiedad definitoria al comportamiento de sus divisores, en concreto, de sus divisores propios, es decir, entre los divisores no se considera al propio número. Estuvimos hablando de los números perfectos, abundantes, deficientes, casi perfectos, multi-perfectos, ambiciosos, sublimes, amigos, novios, sociables, intocables, prácticos, raros, e incluso, poderosos.

En esta entrada vamos a hablar de una serie de familias de números que podríamos denominar en su conjunto como narcisistas, aunque esta sea la denominación particular de una de esas familias. Estos números tienen la propiedad de que, si se toman las cifras que componen cada uno de ellos, después se elevan estas a ciertas potencias y se suman los resultados, se obtiene de nuevo el número.
Recordemos que una persona narcisista es aquella que “cuida demasiado de su arreglo personal, o se precia de atractivo, como enamorado de sí mismo” y el concepto viene del mito griego en el cual el joven y apuesto Narciso se enamoró de su propia imagen reflejada en el agua. En el concepto de números narcisistas la imagen reflejada sería la suma de las potencias de sus cifras, que, al ser el propio número, sería como el enamoramiento de Narciso de su propia imagen reflejada.

Empecemos este recorrido por la familia de números que recibe precisamente el apelativo de números narcisistas. Esta familia está formada por aquellos números que son iguales a la suma de las potencias de sus cifras elevadas a la cantidad de cifras que tiene el número. Por ejemplo, el número 153 es un número narcisista, puesto que, teniendo 3 cifras, que son 1, 5 y 3, se cumple que 13 + 53 + 33 = 1 + 125 + 27 = 153; o también, el número 1634, ya que 14 + 64 + 34 + 44 = 1 + 1296 + 81 + 256 = 1.634.
Los números narcisistas menores que 100.000 son: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1.634, 8.208, 9.474, 54.748, 92.727 y 93.084.
Fijémonos en uno en concreto, el número narcisista 8.208. Este ha alcanzado una cierta fama por haber aparecido en la serie televisiva Los Simpson. Como puede leerse en el libro Los Simpson y las matemáticas del matemático y divulgador Simon Singh, la historia de ese y otros dos números que aparecen en un capítulo de la temporada 17 de esta serie es muy curiosa.
Dentro de la comunidad matemática es conocido que algunos de los guionistas y productores de la serie Los Simpson, así como de la serie Futurama, tienen estudios de matemáticas, y en general, de ciencias, lo que ha motivado que en ambas series aparezcan muchísimas referencias matemáticas. Simon Singh cuenta como, en particular, la profesora Sarah Greenwald, de la Universidad Estatal de los Apalaches, y el profesor Andrew Nestler, de la Universidad de Santa Mónica, empezaron a recoger todas esas referencias y a utilizarlas en sus clases de matemáticas. Cuando esto llegó al oído de los guionistas de la serie Los Simpson, en 2005, decidieron invitarlos a la lectura de un futuro episodio, ese que tendría el título Marge, Homer y el deporte en pareja. Cuando los dos invitados se marcharon, los guionistas se percataron de que en ese episodio no habían incluido ninguna referencia matemática, lo cual les pareció que había sido algo descortés hacia sus invitados y decidieron revisar el guion e incluir un guiño a las matemáticas.

Como se puede ver en la anterior imagen de ese capítulo, decidieron incluir en la pantalla del estadio de béisbol, una mención a la cantidad de público asistente, dando cuatro opciones. La primera 8.191, que es lo que se conoce como un número primo de Mersenne, los cuales son de la forma 2p – 1, en concreto, 213 – 1 = 8.191. La segunda es 8.128, que es un número triangular (véase la entrada El asesinato de Pitágoras, historia y matemáticas (y II)). La tercera cantidad era el número narcisista 8.208, que verifica que 8.208 = 84 + 24 + 04 + 84. La última opción era simplemente que no se podía conocer esa cantidad.
Es fácil observar que solo existe un número finito de números narcisistas. Veámoslo. Si tomamos un número con n cifras, se tiene que ese número es mayor que 10n – 1 y menor que 10n. Por otra parte, la suma de las potencias de sus cifras elevadas a la cantidad de cifras del número alcanza como mucho el valor de 9n + … + 9n (sumado n veces) = n x 9n. Pero resulta que para n > 60, se tiene que n x 9n < 10n – 1, luego la suma de las potencias de las cifras del número elevadas a la cantidad de cifras nunca podrá alcanzar al número. Es decir, no existen números narcisistas con más de 60 cifras.
De hecho, solamente hay 88 números narcisistas (puede verse aquí la lista completa), como fue demostrado por D. T. Winter, en 1985. Además, el mayor de ellos solamente tiene 39 cifras, es
115.132.219.018.763.992.565.095.597.973.971.522.401.
El matemático británico G. H. Hardy (1877 – 1947), en su libro Apología de un matemático, dice en referencia a estos números…
Se trata de hechos excepcionales, ideales para las columnas de acertijos y similares que aparecen en la sección de pasatiempos del periódico para entretener a los aficionados a las matemáticas, pero no hay nada en ellos que atraiga mucho a un matemático.

Este concepto puede extenderse a una familia un poco más amplia, la de los números que son iguales a la suma de las potencias de sus cifras elevadas a una cantidad fija cualquiera, no necesariamente la cantidad de cifras del número, que es el caso de los números narcisistas. Por ejemplo, el número 4.150, que puede expresarse como la suma de las potencias quintas de sus cifras (que son solo cuatro), así 45 + 15 + 55 + 05 = 1.024 + 1 + 3.125 = 4.150. En una nota en la revista Mathematical Gazette, de 1968, se sugiere el nombre de “powerful numbers”, que es el mismo nombre que reciben los números que en la anterior entrada del Cuaderno de Cultura Científica, Los números enamorados, se denominaron poderosos, por lo que llamaremos a estos otros, números potentes. Por otra parte, en el libro Mathematics on vacation, su autor, el químico, editor y matemático recreativo Joseph Madachy (1927 – 2014), les llama números “invariantes digitales perfectos”.
Los números potentes menores de 100.000 son: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1.634, 4.150, 4.151, 8.208, 9.474, 54.748, 92.727 y 93.084, solamente dos más que los narcisistas, a saber, 4.150 y 4.151. El siguiente número poderoso, que además no es narcisista, es 194.979 = l5 + 95 + 45 + 95 + 75 + 95.
En la enciclopedia on-line de sucesiones de números enteros, en la información sobre la sucesión A023052, aparece un listado de los 255 números potentes conocidos. El más grande, que además no es narcisista, tiene 105 cifras y se obtiene al elevar cada una de sus cifras a la potencia 109 y sumarlas. Es …
926.141.173.758.288.802.620.975.817.393.837.795.715.817.835.556.117.230.343.321.424.553.048.655.411.019.641.033.929.959.544.403.221.763.375
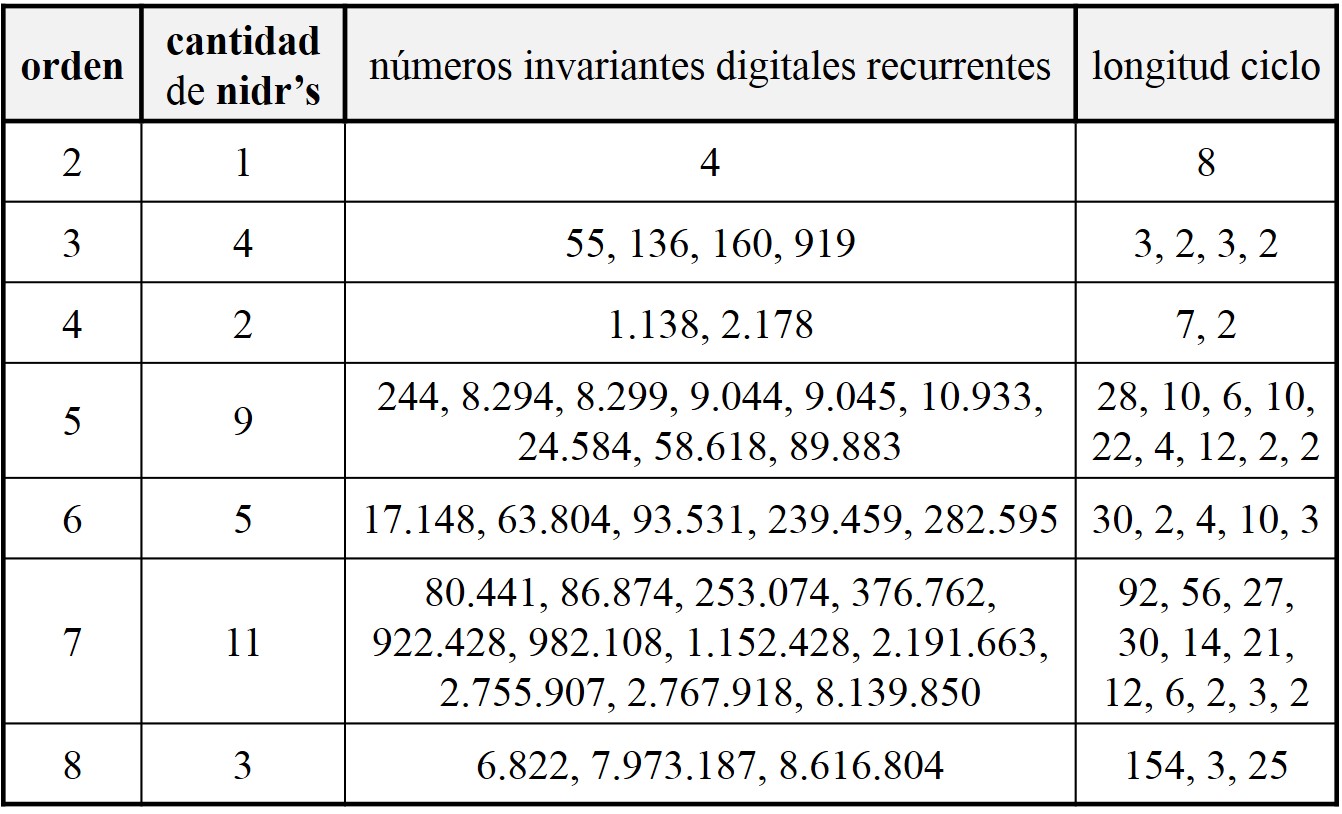
A raíz del concepto de número invariante digital perfecto, Joseph Madachy define los “números invariantes digitales recurrentes”, que podríamos denominar también números potentes recurrentes. Un número es un invariante digital recurrente, de orden k, si al construir la sucesión de números, empezando por el mismo, formados por las sumas de las potencias k-ésimas de las cifras del número anterior, se llega de nuevo al número original en un número finito de pasos, llamado longitud del ciclo. Por ejemplo, el número 55 es un invariante digital recurrente de orden 3, ya que 53 + 53 = 250, 23 + 53 + 03 = 133 y 13 + 33 + 33 = 55, siendo longitud del ciclo igual a 3.
Veamos un ejemplo de orden 4, el número 1.138. Calculemos la sucesión asociada, 14 + 14 + 34 + 84 = 4.179, 44 + 14 + 74 + 94 = 9.219, 94 + 24 + 14 + 94 = 13.139, 14 + 34 + 14 + 34 + 94 = 6.725, 64 + 74 + 24 + 54 = 4.338, 44 + 34 + 34 + 84 = 4.514 y regresamos al origen, después de un ciclo de longitud 8, 44 + 54 + 14 + 44 = 1.138.
Otra familia de números relacionada con los números narcisistas, pero a la que nadie parece haber bautizado, son aquellos números que son iguales a la suma de las potencias de sus cifras elevadas a la posición que ocupan en el número, empezando por la izquierda. Por ejemplo, los números 89, 175, 2.427 y 2.646.798 son de estos números, ya que:
81 + 92 = 8 + 81 = 89,
11 + 72 + 53 = 1 + 49 + 125 = 175,
21 + 42 + 23 + 74 = 2 + 16 + 8 + 2.401 = 2.427, y
21 + 62 + 43 + 64 + 75 + 96 + 87 =
2 + 36 + 64 + 1.296 + 16.807 + 531.441 + 2.097.152 = 2.646.798.
De nuevo, se puede demostrar que esta familia de números es finita. Más aún, no puede haber números de esta familia con más de 22 cifras. Veámoslo.
Si tenemos un número con n cifras, entonces el número es mayor que 10n – 1 y si además pertenece a esta familia, será menor que 9 + 92 + … + 9n, pero, por la fórmula para la suma de los primeros números de la serie geométrica, esta suma es igual a 9 x (9n – 1) / 8 < 9n + 1 / 8. En consecuencia, 10n – 1 < 9n + 1 / 8, que nos lleva, tomando logaritmos, a que n < 22,95 (aprox).
De hecho, solo hay 19 números que verifiquen esta propiedad: 1, 2, 3, 4, 5, 6, 7, 8, 9, 89, 135, 175, 518, 598, 1.306, 1.676, 2.427, 2.646.798 y 12.157.692.622.039.623.539, y el mayor tiene 20 cifras.
Otra familia de números relacionada con los números narcisistas es la formada por los números de Munchausen, aquellos números que son iguales a la suma de sus cifras elevadas a ellas mismas. Por ejemplo, el número 3.435 es un número de Munchausen, ya que 33 + 44 + 33 + 55 = 3.435.
El nombre fue sugerido por el matemático e ingeniero de software holandés Daan van Berkel, en su artículo On a curious property of 3435 (2009), en referencia al barón de Munchausen. En los números de Munchausen cada cifra se eleva a sí misma, de la misma forma que el barón de Munchausen se eleva a sí mismo, tirando de su coleta, con lo cual consigue volar y evita caer en una ciénaga.

Esta es una propiedad muy rígida. El único número de Munchausen, salvo el número 1 que lo es trivialmente, es el número 3.435, como demostró Daan van Berkel. Luego, podemos decir que este es un número muy especial.
Aunque si observamos la definición nos encontramos con un problema. Si una de las cifras del número es el 0, entonces tenemos que sumar 00 y esto es un problema. ¿Cuánto vale 00? Aunque es una polémica no cerrada del todo, la posición de la comunidad matemática es que ese valor debe ser 1. En ese caso, como demostró Daan van Berkel, solo hay dos números de Munchausen 1 y 3.435.
Sin embargo, si admitiésemos que 00 = 0, o modificamos la definición para que solo se considerasen las cifras no nulas, entonces habría otro número de esta familia, el 438.579.088, que verifica que
44 + 33 + 88 + 55 + 77 + 99 + 88 + 88 = 438.579.088.

También se pueden definir los números de Munchausen opuestos, es decir, aquellos números que son iguales a la suma de sus cifras elevadas a ellas mismas, pero no cada una con la suya, sino en el sentido opuesto. Por ejemplo, si consideramos el número 325, sus cifras son 3, 2 y 5, y vamos a tomar sus potencias elevadas a las cifras, pero en el orden opuesto, 5, 2, 3, quedando 35 + 22 + 53 = 243 + 4 + 125 = 372, luego este número no es de Munchausen opuesto. De nuevo, existen solamente dos números en esta familia:
48.625 = 45 + 82 + 66 + 28 + 54,
397.612 = 32 + 91 + 76 + 67 + 19 + 23.

Lo cierto es que el concepto de número narcisista ha generado una enorme familia de generalizaciones. A continuación, haremos un breve repaso por algunas de ellas.
A. Suma de dos cuadrados. Si existiera un número narcisista con dos cifras, lo cual ya sabemos que no existe, entonces este sería igual a la suma de los cuadrados de sus cifras. Se puede generalizar este concepto para números de más de dos cifras, pero dividiendo al número en dos “mitades” de cifras. Es decir, a esta familia pertenecen los números que son iguales a las sumas de los cuadrados de dos “mitades” del número. Veamos algunos ejemplos:
1233 = 122 + 332, 8833 = 882 + 332, 5.882.353 = 5882 + 23532,
1.765.038.125 = 17.6502 + 38.1252, 116.788.321.168 = 116.7882 + 321.1682.
B. Suma de tres cubos. De forma análoga, se pueden considerar aquellos números que son iguales a la suma de los cubos de tres “tercios” del número.
22 18 59 = 223 + 183 + 593,
166 500 333 = 1663 + 5003 + 3333.
C. Números factoriones. Estos números son aquellos que son iguales a la suma de los factoriales de sus cifras. Por ejemplo, 145 es un factorión, ya que
1! + 4! + 5! = 1 + 24 + 120 = 145.
Los números 1 y 2 son trivialmente números factoriones, ya que 1! = 1 y 2! = 2. Y el número 40.585 también es un número factorión, ya que
4! + 0! + 5! + 8! + 5! = 24 + 1 + 120 + 40320 + 120 = 40.585.
Resulta que estos son los únicos factoriones que existen. Supongamos que tenemos un número de n cifras, entonces este es mayor que 10n – 1, pero si es un número factorión, entonces es menor que la mayor suma posible de los factoriales de sus dígitos, que es n x 9!, de donde, 10n – 1 < n x 9!. Pero resulta que, para n = 8 se obtiene que 107 = 10.000.000 > n x 9! = 2.903.040, luego no existen números factoriones de 8 cifras. Y, por inducción, se puede demostrar que ocurre para todos los n mayores o iguales que 8. Para n = 7, la suma máxima de los factoriales de las cifras que se puede obtener es 7 x 9! = 2.540.160, luego solo hay que comprobar los que son menores que esta cantidad. Y solo existen los cuatro anteriores.
D. Pares de números, o números “amigos”, para estas propiedades.
Por ejemplo, un par de números tales que la suma de los cuadrados de dos “mitades” de cada uno de ellos da el otro número, como los números 3.869 y 6.205, para los cuales
382 + 692 = 1.444 + 4.761 = 6.205 y 622 + 052 = 3844 + 25 = 3.869,
o el par de números
5.965 = 772 + 062 y 7.706 = 592 + 652.
Lo mismo para los cubos,
13 + 33 + 63 = 244 y 23 + 43 + 43 = 136,
o los factoriales, donde los tres números 169, 36.301 y 1.454 forman una cadena:
1! + 6! + 9! = 36.301, 3! + 6! + 3! + 0! + 1! = 1.454 y 1! + 4! + 5! + 1! = 169.
E. Números narcisistas salvajes. Estos números, al igual que los narcisistas, pueden ser expresados a partir de sus cifras, pero de una forma particular, las cifras deben de aparecer en el orden que aparecen en el número y pueden utilizarse las operaciones siguientes, suma, resta, multiplicación, división, potencia, radical y factorial.
Mostremos una pequeña colección de distintos números narcisistas salvajes
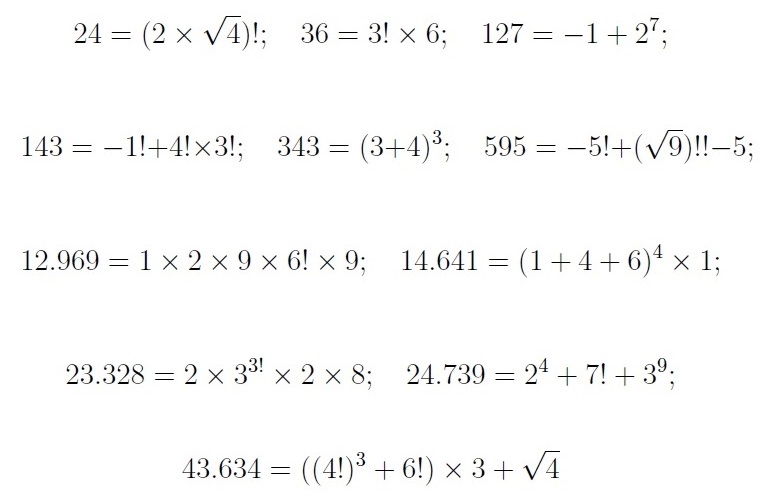
E incluso, se puede considerar que el orden de las cifras sea cualquiera, en cuyo caso se habla de números selfie. Un par de ejemplos serían
34.562 = 2 − (3 − 5) x6! x4!y87.369 = (3! + 7) x8! / 6 + 9.

Bibliografía
1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.
3.- Joseph Madachy, Mathematics on vacation, Charles Scribner’s sons, 1966.
4.- Wolfram Mathworld: Narcissistic Number
5.- Simon Singh, Los Simpson y las matemáticas, Ariel, 2013.
6.- G. H. Hardy, Apología de un matemático, Capitán Swing, 2017.
7.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A0230052 (números potentes o invariantes digitales perfectos)
8.- Wolfram Mathworld: Recurring Digital Invariant
9.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A032799
10.- Daan van Berkel, On a curious property of 3435 (2009) (arXiv:0911.3038)
11.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A046253 (números de Munchausen)
12.- Harvey Heinz, Narcissistic numbers
13.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A014080 (números factoriones)
14.- George D. Poole, Integers and the sum of the factorials of their digits, Mathematics Magazine, vol. 44, n. 5, p. 278-279 (1971).
15.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A193069 (números narcisistas salvajes)
16.- I. J. Taneja, Different Types of Pretty Wild Narcissistic Numbers: Selfie Representations-I, RGMIA Research Report Collection, n. 18, Article 32, pp. 1-43 (2015).
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Hitos en la red #262 – Fluceando
[…] ¿Pueden los números enamorarse de su propia imagen? […]
Números primos gemelos, parientes y sexis (1) — Cuaderno de Cultura Científica
[…] información para mis entradas del Cuaderno de Cultura Científica Los números enamorados y ¿Pueden los números enamorarse de su propia imagen?, descubrí dos familias de números primos especiales, los números primos “parientes” […]
Números errores de impresión — Cuaderno de Cultura Científica
[…] hace un año escribí la entrada ¿Pueden los números enamorarse de su propia imagen? decidí dejar para más adelante el hablar de los números conocidos como “errores de […]
Los números insólitos — Cuaderno de Cultura Científica
[…] numéricas, como los números narcisistas (sobre los que también podéis leer en la entrada ¿Pueden los números enamorarse de su propia imagen?), que son aquellos números que son iguales a la suma de las potencias de sus dígitos elevados a […]
Los números de la suerte — Cuaderno de Cultura Científica
[…] entrada La sucesión de Levine), los números narcisistas (sobre los que puede leerse en la entrada ¿Pueden los números enamorarse de su propia imagen?), los números de Bell relacionados con la poesía (véase la entrada ¿Cuántas estructuras […]