Había pensado empezar esta entrada del Cuaderno de Cultura Científica diciendo que el verano es un buen momento para jugar a cualquier tipo de juego, ya sea un juego popular, de ingenio, de estrategia, de azar, de construcción, solitario, matemático o del tipo que sea, aunque la verdad es que cualquier época del año es un buen momento para jugar. No nos olvidemos nunca de jugar.
En otras entradas de la sección Matemoción ya hemos hablado de algunos juegos, como el molino o alquerque de nueve (en la entrada Mujeres jugando (el juego del molino) relacionada con un cuadro del Museo de Bellas Artes de Bilbao), el tangram (por ejemplo, en las entradas Tangram o Un teorema sobre el tangram), el tchuka ruma (en la entrada Tchuka Ruma, el mancala solitario), el juego coreano kono (en la entrada El juego coreano kono), …

… el salto de la rana, el cinco por cinco, veinticuatro, o el puzle dieciséis inglés (en El salto de la rana y familia), el juego Vee-21 (en la entrada Embaldosando con L-triominós (Un ejemplo de demostración por inducción)), el clásico y universal mancala (en Juegos del mundo: el mancala), el Tetris (en Tetris, embaldosados y demostraciones), algunos juegos con tabletas de chocolate (como los comentados en la entrada Juegos matemáticos con tabletas de chocolate), el rompecabezas geométrico cubo soma (en El cubo soma: diseño, arte y matemáticas), el juego de cartas SET (cuyo análisis matemático presentamos en dos entradas, Matemáticas en el juego de cartas SET (1) y Matemáticas en el juego de cartas SET (2)), el juego probabilístico que analizó el matemático inglés Arthur Cayley, la ratonera (explicado en la entrada La ratonera, el juego de Cayley), el Sim (en El juego del Sim), el solitario locura instantánea (en la entrada Locura instantánea, un rompecabezas con cubos de colores), el tradicional juego de la morra (en La morra, jugando a contar con los dedos), algunos rompecabezas matemáticos (en las entradas Rompecabezas matemáticos con números y Más rompecabezas matemáticos con números) o el margarita y el bloqueado (analizados en la entrada La simetría como estrategia ganadora: la margarita y bloqueado).
En esta entrada del Cuaderno de Cultura Científica me ha parecido una buena idea recuperar un juego tradicional, estos son siempre una fuente de inspiración y de entretenimiento, que analicé en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos (RBA, 2015), el pong hau ki.

El pong hau ki es un juego tradicional chino, que también encontramos en Corea, con el nombre ou moul ko no, en Tailandia como sua tok tong o en la India como do guti, cuyo tablero y forma de juego nos recuerda al clásico tres en raya. En Europa no se empezó a jugar hasta más recientemente, quizás en la época medieval, con el nombre la herradura, así como una variación más moderna de este, el madelinette.
El tablero del pong hau ki está formado por cinco vértices, los cuatro de un cuadrado y el dado por la intersección de las dos diagonales del mismo, y siete aristas que los unen, todas las posibles, menos uno de los lados del cuadrado (véase la imagen de arriba o el esquema de abajo). Hay dos fichas de cada color (por ejemplo, blancas y negras), colocadas inicialmente como se muestra en la siguiente imagen, y cada color le corresponde a un jugador.
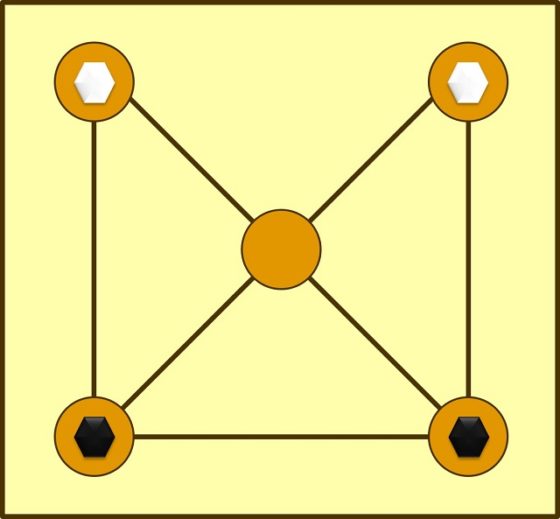
Las reglas del pong hau ki son las siguientes. Cada uno de los dos jugadores, por turnos, mueve una ficha de su color hacia la casilla adyacente que esté vacía. Por ejemplo, en la posición inicial, tanto las blancas como las negras, si empiezan la partida, solo pueden mover una de sus fichas a la casilla central. Gana el jugador que consigue bloquear las dos fichas de su oponente, de forma que este no pueda mover a la casilla libre.
Se considera que este es un juego infantil por su sencillez, como ocurre con el tres en raya o el salto de la rana, pero al igual que estos, tiene más interés del que pueda parecer a primera vista.
Empecemos analizando cuál es el número de posiciones posibles en el juego ou moul ko no. Tenemos cuatro fichas que debemos colocar en el tablero y dejar un hueco vacío. Si todas las fichas fuesen distintas (por ejemplo, las denominamos blanca 1, blanca 2, negra 1 y negra 2) y marcásemos la casilla vacía con una ficha trasparente, entonces el número de formas de colocar las cinco fichas en las cinco casillas sería el factorial de 5, denotado en matemáticas como 5!, cuyo valor es 5! = 5 x 4 x 3 x 2 x 1 y que son el número de permutaciones de cinco elementos (véase El problema matemático de las cartas extraviadas). Sin embargo, las dos fichas blancas son iguales, luego podemos intercambiar las casillas en las que están y sigue siendo la misma posición, luego debemos dividir entre dos. Lo mismo para las fichas negras. De hecho, hemos obtenido la regla para calcular las permutaciones con repetición. En consecuencia, hay 30 posiciones distintas en el juego, ya que:
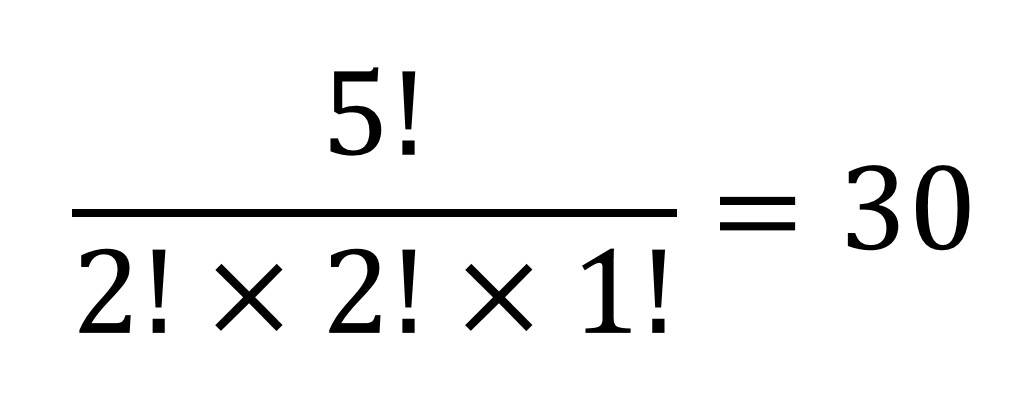
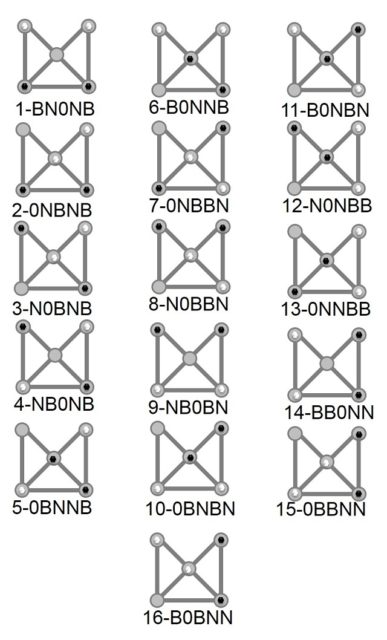
Por otra parte, si miramos la simetría respecto al eje vertical central del tablero, hay dos posiciones que son simétricas respecto a ese eje, es decir, la parte de la izquierda de la posición es igual a la parte de la derecha (que se corresponden con las posiciones 1 y 9 de la siguiente imagen), y catorce pares de posiciones relacionadas, esto es, al intercambiar las fichas de un lado y otro del eje se pasa de una posición a la otra (por ejemplo, la posición 2 de la siguiente imagen –las dos fichas negras abajo, una ficha blanca en medio y una ficha blanca en la posición de arriba a la derecha– se corresponde con la posición simétrica siguiente: las dos fichas negras abajo, una ficha blanca en medio y una ficha blanca en la posición de arriba a la izquierda). Luego, esencialmente tenemos que hay 16 posiciones distintas (salvo simetría) en el sua tok tong.
Si numeramos las casillas del 1 al 5, de arriba abajo y de izquierda a derecha, y etiquetamos cada posición diciendo qué ficha está en cada casilla (B para blanca, N para negra y 0 para vacía), por ejemplo, BN0NB es la posición inicial, podemos listar las 16 posiciones del juego.
El matemático Philip D. Straffin, en su artículo Position graphs for Pong Hau K’i and Mu Torere (Mathematics Magazine, 1995), analizó mediante grafos (véase Locura instantánea, un rompecabezas con cubos de colores o El problema de los tres caballeros y los tres criados), la estrategia ganadora del Pong Hau Ki. Cada una de las dieciséis posiciones del juego es un vértice del grafo y existe una arista entre dos vértices si es posible realizar un movimiento que lleve de una posición a otra. El grafo es además etiquetado, puesto que cada arista llevará la etiqueta B o N, dependiendo de si el movimiento lo realiza el jugador que juega con blancas, o el que juega con negras. El grafo no es dirigido puesto que el movimiento entre dos posiciones puede ser en ambos sentidos.
En consecuencia, el grafo asociado a la herradura, teniendo en cuenta las dieciséis posiciones esenciales del mismo, es el siguiente.
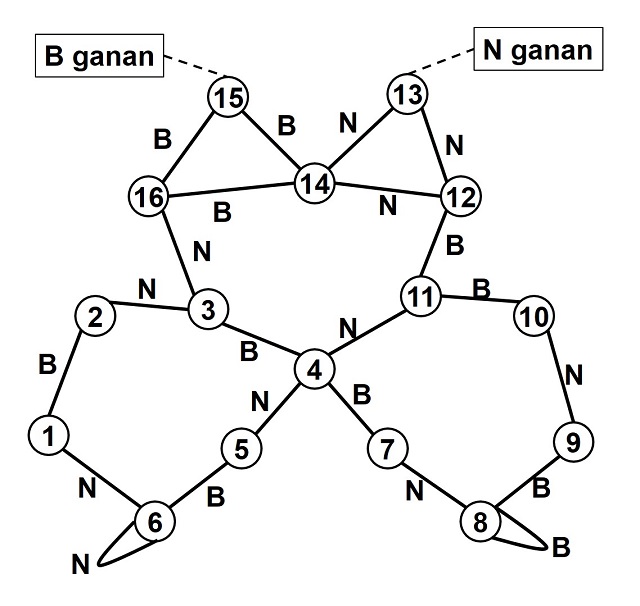
Solo existe una posición ganadora para las blancas, si les toca mover a las negras, que es la posición 15, 0BBNN. Lo mismo para las negras, si mueven blancas, la posición 13, 0NNBB (vemos que es la misma configuración, solo se intercambia la posición de las casillas de las fichas blancas y negras). Para que las blancas lleven la partida a la posición 15, tienen que hacerlo a través de las posiciones 14 o 16, sin embargo, las negras pueden evitar esas posiciones. Lo mismo ocurre para las negras, en relación a la posición 13. De hecho, el juego, bien jugado, se mantendrá en un movimiento infinito entre los ciclos 1-2-3-4-5-6 y 4-11-10-9-8-7. Lo cual implica que el pong hau ki siempre terminará en tablas, salvo que se cometa un error, como ocurre con el tres en raya.
Una forma alternativa de jugar a la herradura, para darle un poco más de interés, es que el tablero esté inicialmente vacío y que los jugadores empiecen colocando por turnos cada una de sus fichas en el mismo. Si observamos el grafo anterior, la táctica para no perder es la misma que partiendo de la posición inicial dada (posición 1), solo que ahora hay que evitar las posiciones conflictivas al ir colocando las fichas al principio. Si empiezan las blancas, las negras evitarán las posiciones en las que tocándole mover a las blancas ganen, que son las posiciones 14 y 16, y las blancas evitarán la posición 13, que es la posición ganadora para las negras si mueven blancas (o, en ambos casos, sus posiciones simétricas).
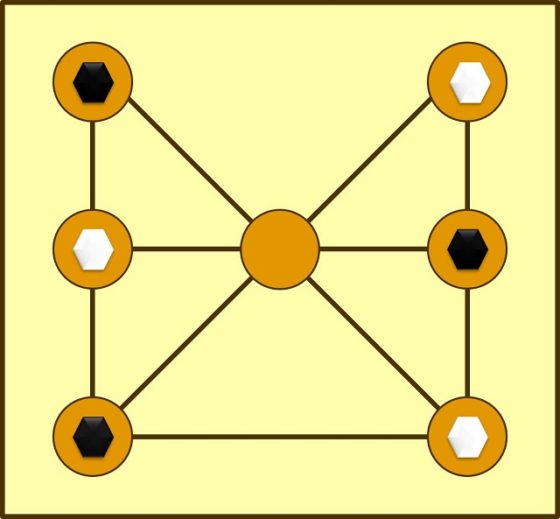
El madelinette es una versión más compleja e interesante del juego de la herradura, que podría haber sido inventada por el militar y matemático aficionado francés Henri August Delannoy (1833-1915). El madelinette se juega con tres fichas de cada color y al tablero se le añade el segmento horizontal que pasa por el centro, obteniéndose así un total de siete casillas (como se muestra en la imagen anterior). Según el matemático francés Édouard Lucas (1842-1891), en sus Recreaciones matemáticas, las posiciones ganadoras, perdedoras y de tablas de los juegos la herradura y el madelinette fueron estudiadas por Henri Delannoy.
El madelinette se puede jugar a partir de la posición inicial que aparece en la anterior imagen, o con el tablero vacío, y el objetivo es de nuevo bloquear las fichas del jugador contrario.
Con un argumento similar al del juego pong hau ki se obtiene que el número de posiciones distintas del madelinette es

que dan lugar a 70 parejas de posiciones simétricas, una de la otra, respecto al eje vertical central.
Si pintásemos el grafo etiquetado asociado a este juego, resulta ser más complejo que el del pong hau ki, puesto que de cada posición (vértice del grafo) podemos pasar mediante un movimiento a más posiciones que antes. Por ejemplo, si empezasen moviendo las fichas negras, de la posición inicial se podría pasar a una de las siguientes tres posiciones siguientes. Además, aunque en la primera posición las blancas solo tendrían un movimiento posible, en las otras dos posiciones existirían dos opciones de movimiento.
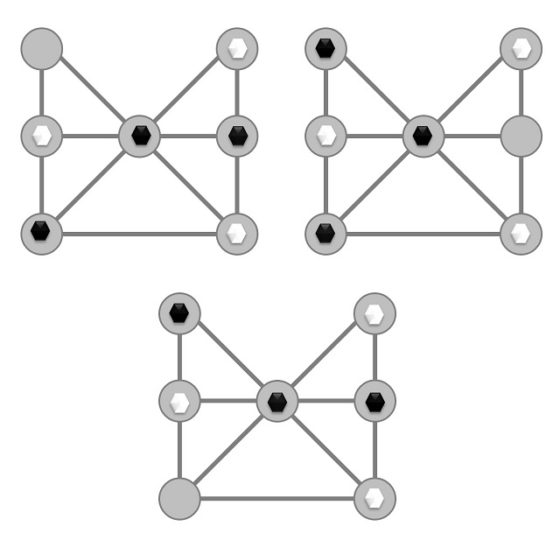
Delannoy estudió qué posiciones son ganadoras, perdedoras o que terminan en tablas, jugando bien, suponiendo que mueven blancas (un razonamiento simétrico se obtiene si mueven negras). De las 70 posiciones diferentes (salvo simetría) hay 21 ganadoras para las blancas, 12 para las negras y 37 que serán empates.
A continuación, como ejemplo mostramos tres posiciones, una ganadora para las blancas, otra ganadora para las negras y otra que termina en empate, suponiendo que mueven blancas:
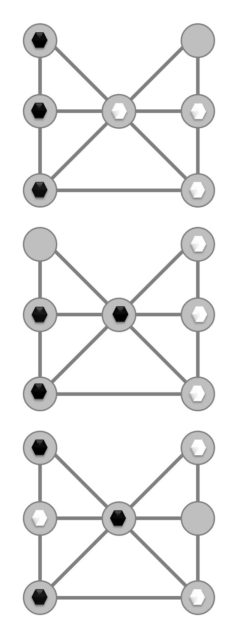
Al contrario que en la herradura, aquí hay más posiciones ganadoras para ambos colores, hay muchas más combinaciones y es fácil cometer fallos o despistes. Por eso mismo, el juego se hace más interesante.
Para terminar, lo que decimos siempre, lo mejor de un juego es jugar y disfrutarlo. Divertíos.
Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Philip D. Straffin, Position graphs for Pong Hau K’i and Mu Torere, Mathematics Magazine, vol. 68, n. 5, 1995.
3.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica