Si tu estantería se parece un poco a la de mi casa, como mínimo uno de sus estantes estará lleno de CDs. Pero si tu rutina se parece un poco a la mía, probablemente hace ya tiempo que no utilizas esos CDs para escuchar música. Al menos, en mi caso, estos artilugios del siglo XX han pasado a convertirse en preciosos recuerdos de conciertos aún mejores, pero su valor práctico está cada vez está en más entredicho. El siguiente en caer será mi colosal archivo de ficheros mp3, aplastado por el peso de otro mucho mayor: la base de datos de Spotify.

Sin embargo, hay algo en lo que Spotify nunca batirá a los CDs, una utilidad quizás no tan conocida pero francamente sorprendente: la capacidad de los CDs para hacer espectroscopía. Ya verás, pruébalo en casa: quita un poco el polvo de ese viejo estante y elige un CD cualquiera; ilumínalo con una linterna y… ¡voilá! el arcoiris: aparecen los colores de los que se compone esa luz. Puedes verlos directamente sobre el CD o, apagando las luces, proyectando la reflexión que se produce en el CD sobre la pared. La segunda opción, para mi gusto, es la más impresionante.

Lo que sucede es que los CDs tienen una serie de ranuras, de pistas enrolladas sobre sí mismas de una anchura similar a la longitud de onda de la luz. Dependiendo del ángulo con que incide la luz incide, se refleja una longitud de onda u otra, es decir, un color u otro. Por eso, cuando vemos la luz reflejada en el CD, los colores aparecen en la pared separados, abiertos como en un abanico.

El primero en observar este fenómeno fue Newton en el siglo XVII. Aunque, evidentemente, Newton no utilizó un CD: en su lugar lo que usó fue un prisma. El fenómeno es el mismo: el cristal, con su característico índice de refracción, provoca que la luz se tuerza (cambie su trayectoria) de manera distinta según su longitud de onda y, de nuevo, los colores aparecen desplegados al atravesarlo, mostrando lo que se conoce como el espectro de la luz. Gracias a este fenómeno, Newton pudo demostrar que la luz blanca es la suma de todos esos colores.

Sin embargo, si alguna vez habéis tenido ocasión de jugar con un prisma o, si habéis mirado durante un buen rato el arcoiris… sabréis que no resulta sencillo contar cuántos colores hay ahí. No es fácil determinar dónde empieza y dónde acaba el naranja, por ejemplo, o cuál es la frontera entre el verde y el azul. A pesar de los libros de colorear que nos daban de niños: la luz, el arcoiris no tiene escalones, es un continuo. Y, sin embargo, Newton no se limitó a decir que luz blanca era la suma de los demás colores sino que, además, decidió ponerles número: el espectro luminoso estaba formado, exactamente, por siete colores, los siete colores que hoy decimos que tiene el arcoiris.

A pesar de no tratarse de una observación científica, objetivable, el número siete no era en absoluto casual. Para estudiar la luz, Newton se basó en el sonido y siete son las notas que tiene una escala musical en la tradición occidental. Concretamente, Newton se basó en una escala dórica. Esta escala tiene dos semitonos, dos sonidos más cercanos entre sí, justo entre lo que correspondería al rojo y el amarillo, y al azul y el violeta. Este es el motivo por el que tenemos colores tan secundarios en nuestro arcoiris como el naranja, es el motivo que todos los niños, desde hace 3 siglos, tienen que aprenderse el color añil… aunque nadie sepa muy dónde está.

Valses nobles et sentimentales, No.2 de Ravel, compuesto sobre la escala dórica.

Por lo demás, la teoría de Newton sobre la luz no era del todo correcta. Newton apostó que la luz eran partículas y hoy sabemos que también tiene propiedades ondulatorias. Sin embargo, justo en esta analogía musical, hasta cierto punto acertó: el color es a la luz, lo que las distintas notas son al sonido. Tanto la luz como el sonido son ondas. Y lo que distingue a los distintos colores entre sí es, precisamente, la frecuencia, lo rápido que oscila esa onda, lo mismo que distingue unas notas de otras en el caso del sonido.

Ahora bien, como podemos comprobar con ayuda de un CD, la mayoría de las luces que vemos en nuestro día a día, no están compuestas de un color puro, de una sola frecuencia: las bombillas incandescendentes, el fluorescente de la cocina, los LEDs… cada fuente luminosa tiene su propia composición en colores, su propio espectro. Sólo un láser nos daría una frecuencia única. Exactamente del mismo modo: la mayoría de los sonidos que escuchamos cotidianamente están compuestos por la suma de muchos sonido de distinta frecuencia; cada uno tiene su propio espectro sonoro.

En el caso del sonido no hay un espectrógrafo tan barato y tan casero como el CD para la luz. Sí pueden descargarse bastantes aplicaciones para móvil y, si te gustan un poco los temas relacionados con el sonido, te recomiendo encarecidamente que lo hagas. Pero, sin duda, el mejor analizador de espectros sonoro lo tenemos todos en la cabeza y son nuestros oídos. En el oído hay un órgano, llamado cóclea que es un verdadero portento descomponiendo el sonido en sus distintas frecuencias.

Gracias a ello podemos reconocer el timbre de los sonidos, podemos distinguir un violín de un trombón, entre la voz de una amiga o la de tu hermana, o, por ejemplo, el sonido de las distintas vocales. Quizás por ello, nuestro oído sea tan bueno en esta tarea: todos los fonemas de un idioma son una cuestión de timbre. En concreto, las vocales se distinguen únicamente por la intensidad relativa de sus componentes espectrales, por la distribución de su arcoiris interno. Si me has hecho caso y tienes un analizador de espectros sonoros instalado ya en tu móvil, prueba a cantar una misma nota sobre distintas vocales: verás que los picos no cambian de lugar, sólo de intensidad.

Las vocales son un ejemplo de lo que se conoce como sonidos de tono bien definido. Como definición intuitiva podríamos decir que son los sonidos que se pueden cantar: intenta cantar el sonido de una palmada, o el de una “p”. Difícil, ¿verdad? Son sonidos ruidosos, no tienen una nota que se les pueda asignar con facilidad. Bien, los sonidos de tono bien definido son especialmente interesantes porque su espectro tiene una forma muy peculiar: en lugar de tener un arcoiris continuo de frecuencias, lo que encontramos son una serie de picos. Estos picos, estas frecuencias nos dan información sobre cómo vibra un determinado objeto y la forma del objeto mismo.

Si tomamos, por ejemplo, una cuerda (lo que se suele tomar para modelizar estos sonidos), observaremos sólo puede moverse de determinadas maneras definidas por su propia geometría: sólo puede vibrar como una comba, o por mitades, por tercios… pero nunca de maneras asimétricas, por ejemplo. Por este motivo, el sonido de una cuerda (y los sonidos de tono bien definido en general) está compuesto por una serie de frecuencias muy bien definidas que se relacionan por números enteros: los llamados armónicos. Estos armónicos nos informan sobre los modos de vibración, las formas de moverse del objeto, bien sea una cuerda, nuestras cuerdas vocales o un instrumento de viento.

Esta es la forma que tienen, por ejemplo, los espectros de un clarinete y una flauta:

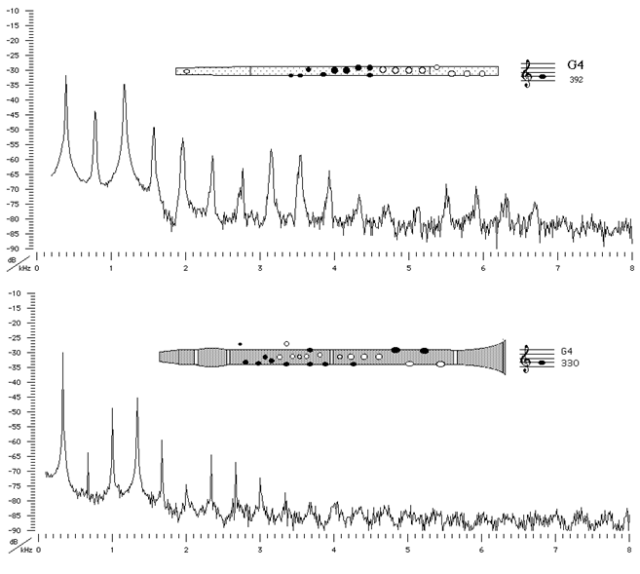
Este, en cambio, es aspecto que tiene el espectro del hidrógeno:

Decíamos antes que la mayoría de fuentes de luz que encontramos en nuestro entorno se dividen un arcoiris más o menos continuo. Sin embargo, en el siglo XIX, los físicos descubrieron que si calentaban suficientemente un gas y miraban su espectro, lo que aparecía no era ese continuo sino una serie de líneas, separadas entre sí, igual que en el caso del sonido. A su vez, la espectroscopia alcanzó suficiente precisión para empezaron a observar, esas mismas líneas, solo que en negativo, como sombras, sobre la luz de las estrellas. Como las líneas coincidían, los físicos pensaron que esta podría ser la clave para descubrir de qué estaba hecho el universo.

Además, aquellas líneas eran sorprendentemente parecidas a los picos de los espectros sonoros ya conocidos. Por eso, lo primero que pensaron fue que aquello debían ser los armónicos de los átomos, sus frecuencias naturales, sus modos característicos de moverse internamente. El físico Johnstone Stoney denominó, incluso, a estas líneas “sobretonos” e intentó ajustarlas a la serie armónica (1/n) propia de los sonidos musicales. En el caso del hidrógeno, concluyó que las tres líneas principales en el rango visible correspondían a los armónicos 20, 27 y 32 de una frecuencia fundamental. Pero para Balmer, estos números resultaban demasiado caprichosos, demasiado “feos”. Por eso se esforzó en encontrar una expresión más bonita (y correcta) que permitiese hallar la frecuencia fundamental del espectro, como en el caso de la cuerda. Así halló la fórmula que lleva su nombre, si bien los modos de vibración que representaba siguieron siendo un misterio.

De nuevo, los físicos no estaban del todo en lo correcto, pero tampoco iban muy desencaminados. De hecho, los electrones dentro de los átomos están restringidos a moverse dentro de una serie de orbitales. Existen modos de vibración permitidos, niveles energéticos permitidos dentro de un átomo para un electrón, comparables a los modos de vibración de una cuerda. En realidad, el espectro de la luz no nos da directamente las frecuencias de estos niveles, sino que nos da una diferencia de frecuencias (por eso hay una resta en la fórmula de Balmer). Esto es así porque lo que llega a nosotros, lo que percibimos a través de la luz son fotones que han saltado de un nivel a otro y que llevan consigo la diferencia de energías entre estos niveles. Pero, finalmente, el fenómeno no es tan lejano: existen modos de vibración en los átomos y, en definitiva, un concepto sonoro, los armónicos, sirvió para intuir y acercar de manera muy temprana, un concepto de física nuclear mucho más complejo.

Desde entonces, los espectros de las estrellas han servido a los científicos para averiguar de qué está hecho el universo. Cada átomo deja su impronta sobre la luz, una huella dactilar inconfundible y característica. Pero también podemos, en honor a la historia, pensar en esos espectros como los timbres del universo y, en los astrofísicos, como verdaderos afinadores de estrellas.

Este post ha sido realizado por Almudena M. Castro (@puratura) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.