Los científicos a menudo nos quejamos, especialmente desde foros como este en el que escribo, del desinterés por la cultura científica que existe en gran parte de la sociedad. Frecuentemente esta falta de interés está relacionada con la sensación de que la ciencia es demasiado difícil para ser comprendida, la creencia de que “la ciencia no es para mí”[1].

Por su reputación de asignatura hueso y su terrible capacidad para traumatizar estudiantes, las matemáticas se llevan la palma en el ránking de “cosas demasiado difíciles”. La idea de la inaccesibilidad de las matemáticas llega a calar incluso entre científicos de otras ramas. Para mayor drama, en todas las ramas de la ciencia surgen problemas matemáticos de forma natural. Abordar este tipo de problemas dando la espalda a las matemáticas suele ser una mala idea. Lo ilustraremos con un ejemplo, un ejemplo bastante extremo:

Sucedió en febrero de 1994, cuando se publicó este artículo en la revista Diabetes Care: «A mathematical model for the determination of total area under glucose tolerance and other metabolic curves», firmado por Mary M. Tai, que pasaría inmediatamente a la historia de la ciencia, aunque por motivos poco halagadores.

El artículo trata del análisis de curvas metabólicas. Simplificando mucho, la diferencia entre un paciente sano y un paciente con diabetes es que este último es mucho más lento eliminando de su sangre la glucosa recién consumida. Una forma fácil de visualizar esto es midiendo su concentración de glucosa en sangre, pongamos, cada hora, y representándola en figuras como la siguiente:

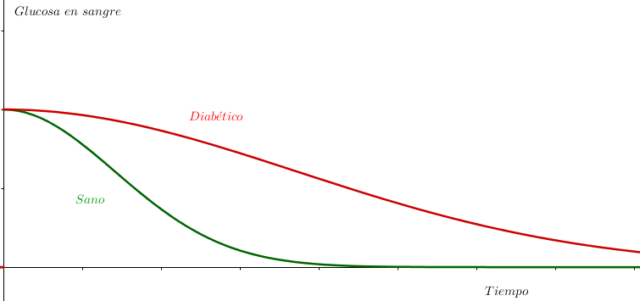
La forma de este tipo de curvas es, pues, de vital importancia. Concretamente, el problema que se pretende resolver en el artículo y, de hecho, se resuelve, es el de determinar el área bajo una de estas curvas. El método propuesto consiste en rellenarla con pequeños trapecios y sumar las áreas de cada uno de ellos, como se aprecia en la figura:

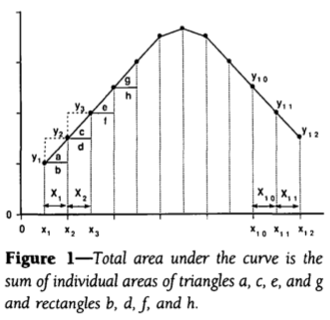
Lo curioso del caso es que el método propuesto como novedoso, y bautizado nada menos que como “modelo de Tai”, se conoce desde tan antiguo que resulta difícil establecer la fecha concreta de su descubrimiento. Hay sospechas fundadas de que los Babilonios lo usaban para sus cálculos astronómicos; de lo que no cabe duda de que era un método bien conocido en los tiempos de Euler. En matemáticas se conoce con el nombre, mucho más humilde, de regla del trapecio.

Es posible que todo lo anterior les resulte familiar. En las matemáticas del instituto se estudia algo llamado integral. Las integrales sirven, entre otras cosas, para calcular el área bajo una curva. Es decir: existe un método (conocido desde finales del siglo XVII) enseñado en los libros de texto de secundaria, que responde a la pregunta de investigación que se plantea el artículo[1], y que constituye uno de los pilares de la rama matemática conocida como cálculo infinitesimal. En resumen, se publicó un artículo que redescubría una operación básica con tres siglos de retraso (como mínimo).

Que un artículo como este resultase publicado es, cuanto menos, chocante. Más chocante aún es saber que recibió una apreciable cantidad de citas por parte de colegas, que encontraron el “modelo de Tai” útil para su trabajo. Hubo también colegas que comentaron acertadamente que el artículo estaba redescubriendo (y rebautizando) la regla del trapecio. A estos, la autora responde enrocándose en su posición, considerando la regla del trapecio “mero sentido común” y un conocimiento tan irrelevante “que no es de Premio Nobel”. A pesar de esto, no tiene reparos en reclamar su nombre para el método de “sentido común” pocas líneas más abajo. El resto de respuestas van en la misma línea y tono, dejando claro que no estamos ante un problema de comunicación entre disciplinas. Lejos de ser retractado, las citas del artículo siguen aumentando gracias al revuelo formado, aunque fundamentalmente es citado como ejemplo de ciencia patológica.

Las reacciones habituales que he encontrado cuando he contado esta historia a mis colegas son risa, incredulidad, e incluso algunas veces indignación. Pero yendo un poco más allá de lo superficial, esta historia tiene varias lecturas interesantes.

Para empezar, pone de manifiesto que la falta de cultura científica se da también dentro de la comunidad científica. El hecho de que nadie en todo el proceso de publicación levantase la ceja ante un método con siglos de antigüedad, con un papel central en la historia de la ciencia y descrito en los libros de texto de secundaria, es prueba de ello.

Por otro lado, el problema original es obviamente un problema geométrico básico, que incluso tiene cierto “aroma” a geometría griega. La autora tiene un nivel de matemáticas suficiente para desarrollar desde cero un método aproximado que lo resuelve. Un vistazo a cualquier libro de matemáticas le habría ahorrado tiempo y esfuerzo. ¿Por qué no empezó por ahí?, ¿estamos quizá ante otra forma enrevesada de enfrentar un problema en esencia matemático, pero “dando la espalda a las matemáticas”?

Siendo un poco más sutiles, uno puede preguntarse si realmente es lícito “rescatar” un método conocido para aplicarlo dónde no se ha aplicado antes. Al fin y al cabo, el uso de métodos conocidos en áreas “exóticas” es la esencia de la investigación multidisciplinar. En el caso del artículo mencionado, casi todo el mundo opina que se cruzó una línea roja. Pero, ¿y un artículo que, por ejemplo, rescate un teorema matemático del siglo XIX para llegar a conclusiones sobre un modelo de crecimiento de plankton? En este caso casi todo el mundo opinará que se trata de una investigación totalmente lícita, a pesar de que la novedad de los resultados puede también ponerse en entredicho. Suele ser fácil ver en qué lado de la línea roja estamos, pero no es nada sencillo trazarla.

Y, por último, la anécdota deja patente que el proceso de revisión por pares dista mucho de ser perfecto. Es buena idea mantener un sano escepticismo a todos los niveles, incluso al leer artículos revisados, publicados… e incluso altamente citados.

Seguro que hay más opiniones. Les invito a dejarlas en los comentarios.

Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.

Referencias, citas y más información:

[1] Cuando la ciencia se “disfraza” en forma de historia (véase el extraordinario ejemplo del podcast Catástrofe Ultravioleta o los eventos Naukas) y se rompe esta primera barrera, los resultados son sorprendentes: resulta que la ciencia no solamente interesa a casi todo el mundo, sino que también gusta.

[2] El concepto renacentista de integral es incluso más avanzado que el mostrado en el artículo de 1994, pues en este último se pasan por alto los problemas derivados de escoger anchuras arbitrarias para los trapecios (problema que las integrales evitan usando el concepto de límite para tomar rectángulos infinitamente estrechos).

M. M. Tai, “A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves,” Diabetes Care, vol. 17, no. 2, pp. 152–154, Feb. 1994.