Las pruebas matemáticas basadas en una técnica llamada diagonalización pueden ser implacablemente contrarias, pero ayudan a revelar los límites de los algoritmos.

Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.

Los algoritmos se han vuelto omnipresentes. Optimizan nuestros viajes, procesan pagos y coordinan el flujo del tráfico en Internet. Parece que para cada problema que puede articularse en términos matemáticos precisos, hay un algoritmo que puede resolverlo, al menos en principio.

Pero ese no es el caso: algunos problemas aparentemente simples nunca pueden resolverse algorítmicamente. El científico informático pionero Alan Turing demostró la existencia de estos problemas “incomputables” hace casi un siglo, en el mismo artículo en el que formuló el modelo matemático de computación que lanzó la informática moderna.

Turing demostró este resultado innovador utilizando una estrategia contraria a la intuición: definió un problema que simplemente rechaza todo intento de resolverlo.

«Te pregunto qué estás haciendo y luego digo: ‘No, voy a hacer algo diferente'», explica Rahul Ilango, un estudiante de posgrado en el Instituto de Tecnología de Massachusetts que estudia informática teórica.

La estrategia de Turing se basa en una técnica matemática llamada diagonalización que tiene una historia ilustre. He aquí una explicación simplificada de la lógica de su prueba.

Teoría de cadenas

La diagonalización surge de un truco inteligente para resolver un problema rutinario que involucra cadenas de bits, cada uno de los cuales puede ser 0 o 1. Dada una lista de estas cadenas, todas igualmente largas, ¿se puede generar una nueva cadena que no esté en la lista?

La estrategia más sencilla es considerar cada cadena posible por turno. Supongamos que tienes cinco cadenas, cada una de cinco bits de longitud. Comienza repasando la lista en busca de 00000. Si no está, puedes parar; si está, pasa a 00001 y repite el proceso. Esto es bastante simple, pero lento para listas largas de cadenas largas.

La diagonalización es un enfoque alternativo que construye poco a poco una cadena nueva. Comienza con el primer bit de la primera cadena de la lista e inviértelo; ese será el primer bit de tu nueva cadena. Luego invierte el segundo bit de la segunda cadena y utilízalo como el segundo bit de la nueva cadena, y repite hasta llegar al final de la lista. Los bits que inviertes garantizan que la nueva cadena difiera de cada cadena de la lista original en al menos un lugar. (También forman una línea diagonal a través de la lista de cadenas, lo que da nombre a la técnica).

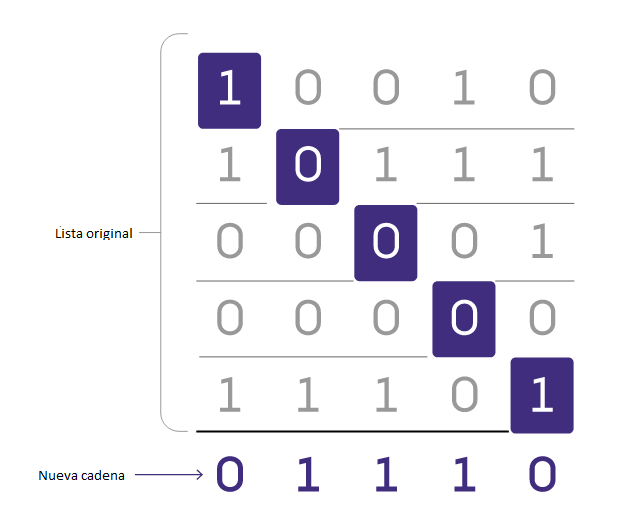
La diagonalización sólo necesita examinar un bit de cada cadena de la lista, por lo que suele ser mucho más rápido que otros métodos. Pero su verdadero poder reside en lo bien que se comporta con el infinito.

“Las cadenas ahora pueden ser infinitas; la lista puede ser infinita; todavía funciona”, afirma Ryan Williams, científico informático teórico del MIT.

La primera persona en aprovechar este poder fue Georg Cantor, el fundador del subcampo matemático de la teoría de conjuntos. En 1873, Cantor utilizó la diagonalización para demostrar que algunos infinitos son más grandes que otros. Seis décadas después, Turing adaptó la versión de Cantor de la diagonalización a la teoría de la computación, dándole un tono claramente a contracorriente.

El juego de la limitación [*]

Turing quería demostrar la existencia de problemas matemáticos que ningún algoritmo puede resolver, es decir, problemas con entradas y salidas bien definidas pero sin un procedimiento infalible para pasar de la entrada a la salida. Hizo que esta vaga tarea fuera más manejable al centrarse exclusivamente en problemas de decisión, donde la entrada puede ser cualquier cadena de ceros y unos y la salida es 0 o 1.

Determinar si un número es primo (divisible sólo por 1 y por sí mismo) es un ejemplo de un problema de decisión: dada una cadena de entrada que representa un número, la salida correcta es 1 si el número es primo y 0 si no lo es. Otro ejemplo es comprobar los programas informáticos en busca de errores de sintaxis (el equivalente a errores gramaticales). Aquí, las cadenas de entrada representan código para diferentes programas (todos los programas se pueden representar de esta manera, ya que así es como se almacenan y ejecutan en los ordenadores) y el objetivo es generar 1 si el código contiene un error de sintaxis y 0 si no lo contiene.

Un algoritmo resuelve un problema sólo si produce la salida correcta para cada entrada posible; si falla aunque sea una vez, no es un algoritmo generalista para ese problema. Normalmente, primero especificarías el problema que deseas resolver y luego intentarías encontrar un algoritmo que lo resuelva. Turing, en busca de problemas irresolubles, le dio la vuelta a esta lógica: imaginó una lista infinita de todos los algoritmos posibles y utilizó la diagonalización para construir un problema pertinaz que frustraría todos los algoritmos de la lista.

Imagina un juego amañado de ’20 preguntas’ [**], donde en lugar de comenzar con un objeto particular en mente, quien responde inventa una excusa para decir no a cada pregunta. Al final del juego, han descrito un objeto definido completamente por las cualidades que le faltan.

La prueba de diagonalización de Turing es una versión de este juego en el que las preguntas recorren la lista infinita de algoritmos posibles, preguntando repetidamente: «¿Puede este algoritmo resolver el problema que nos gustaría demostrar que es incomputable?»

«Es una especie de ‘preguntas infinitas'», comenta Williams.

Para ganar el juego Turing necesitaba elaborar un problema en el que la respuesta fuera no para cada algoritmo. Eso significaba identificar una entrada particular que hiciese que el primer algoritmo generase una respuesta incorrecta, otra entrada que hiciese que el segundo fallase, y así sucesivamente. Encontró esas entradas especiales utilizando un truco similar al que Kurt Gödel había utilizado recientemente para demostrar que afirmaciones autorreferenciales como “esta afirmación no es demostrable” significaban problemas para los fundamentos de las matemáticas.

La idea clave fue que cada algoritmo (o programa) se puede representar como una cadena de ceros y unos. Eso significa, como en el ejemplo del programa de comprobación de errores, que un algoritmo puede tomar el código de otro algoritmo como entrada. En principio, un algoritmo puede incluso tomar su propio código como entrada.

Con esta idea, podemos definir un problema no computable como el de la prueba de Turing: “Dada una cadena de entrada que representa el código de un algoritmo, genera 1 si ese algoritmo genera 0 cuando su propio código es la entrada; de lo contrario, la salida es 0”. Cada algoritmo que intente resolver este problema producirá una salida incorrecta en al menos una entrada, es decir, la entrada correspondiente a su propio código. Eso significa que este perverso problema no puede resolverse mediante ningún algoritmo.

Lo que la negación no puede hacer

Los informáticos aún no habían terminado con la diagonalización. En 1965, Juris Hartmanis y Richard Stearns adaptaron el argumento de Turing para demostrar que no todos los problemas computables son iguales: algunos son intrínsecamente más difíciles que otros. Este resultado lanzó el campo de la teoría de la complejidad computacional, que estudia la dificultad de los problemas computacionales.

Pero la teoría de la complejidad también reveló los límites del método a la contra de Turing. En 1975, Theodore Baker, John Gill y Robert Solovay demostraron que muchas cuestiones abiertas en la teoría de la complejidad nunca pueden resolverse únicamente mediante la diagonalización. La principal de ellas es el famoso problema de las clases de complejidad P y NP, que pregunta si todos los problemas con soluciones fácilmente comprobables también son fáciles de resolver con el algoritmo adecuado.

Los puntos ciegos de la diagonalización son una consecuencia directa del alto nivel de abstracción que la hace tan poderosa. La demostración de Turing no implicaba ningún problema incomputable que pudiera surgir en la práctica; en cambio, inventó un problema de ese tipo sobre la marcha. Otras pruebas de diagonalización están igualmente alejadas del mundo real, por lo que no pueden resolver cuestiones en las que los detalles del mundo real importan.

«Manejan la computación a distancia», explica Williams. «Me imagino a un tipo que se enfrenta a un virus y accede a él a través de una caja de guantes».

El fracaso de la diagonalización fue una indicación temprana de que resolver el problema de las categorías P y NP iba a ser un largo camino. Pero a pesar de sus limitaciones, la diagonalización sigue siendo una de las herramientas clave en el arsenal de los teóricos de la complejidad. En 2011, Williams lo utilizó junto con una serie de otras técnicas para demostrar que cierto modelo restringido de computación no podía resolver algunos problemas extraordinariamente difíciles, un resultado que había eludido a los investigadores durante 25 años. Estaba muy lejos de resolver el problema de las categorías P y NP, pero aun así representó un avance importante.

Si quieres demostrar que algo no es posible, no subestimes el poder de simplemente decir no.

Notas del traductor:

[*] El original en inglés “The limitation game” es un juego de palabras con el título de la película “The Imitation Game” basada en aspectos de la vida y obra de Alan Turing.

[**] En el juego tradicional de ’20 preguntas’ la persona que responde (la “respondedora”) elige algo que las demás jugadoras, las «interrogadoras», deben adivinar. Se turnan para hacer una pregunta a la que la respondedora debe responder «sí» o «no». Ejemplos de preguntas podrían ser: «¿Es más grande que un móvil?», «¿Está vivo?» y, finalmente, «¿Es este bolígrafo?». No se permite mentir. Si una interrogadora adivina la respuesta correcta, gana y se convierte en la respondedora en la siguiente ronda. Si se hacen 20 preguntas sin una respuesta correcta, entonces la respondedora gana y vuelve a ser la persona que responde en otra ronda.

El artículo original, Alan Turing and the Power of Negative Thinking, se publicó el 5 de septiembre de 2023 en Quanta Magazine.

Traducido por César Tomé López