El conocimiento químico viene de antiguo. Hasta hace poco más de un siglo era un conocimiento puramente fenomenológico obtenido en la mayoría de los casos por ensayo y error. Démonos cuenta que la cuantificación en la química empieza a finales del siglo XVIII, con Lavoisier y el uso de la balanza, por lo que no cabría esperar la existencia ni de teoría química propiamente dicha, ni mucho menos, de una teoría de estructura matemática antes de esa fecha. Sin embargo, si nos paramos a definir qué es pensar matemáticamente, podemos encontrar ilustraciones de pensamiento matemático aplicado a la química desde la antigüedad. Y es que para pensar matemáticamente no hacen falta números. Veamos un ejemplo.

La tabla de afinidades de Geoffroy

Siguiendo la filosofía cartesiana del XVII, varios filósofos naturales y matemáticos franceses desarrollaron la idea de un conocimiento químico racional y matematizado. Así, Bernard le Bovier de Fontenelle, el secretario a la sazón de la Académie des Sciences desde 1697, afirmaba en su introducción a la Histoire de l’Académie royale des sciences (1702) que:

“las matemáticas no sólo han producido una infinitud de sus propias verdades, sino que también han producido en las mentes con bastante generalidad un hábito de exactitud y precisión incluso más precioso que todas estas verdades”.

En ese mismo texto Fontenelle sugería la idea de matematizar la química como se había hecho con la geometría (se refiere a la geometría analítica cartesiana), con objeto de poder hacer predicciones. El programa subyacente era legitimar la química como la parte teórica de la “vulgar farmacia” y como compañera respetable de los médicos y su arte.

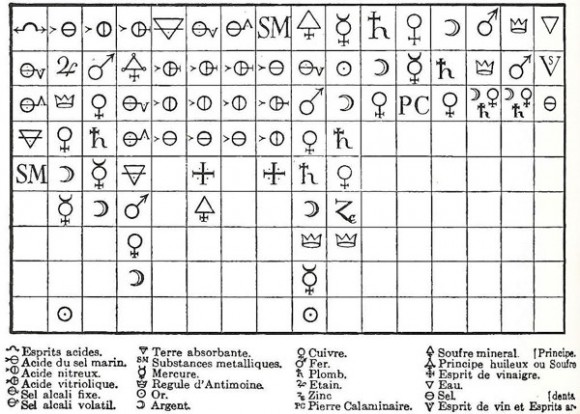
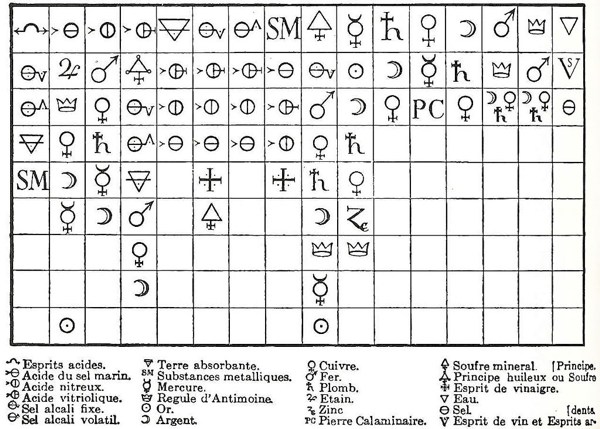
Un miembro de este grupo de filósofos naturales fue Etienne-François Geoffroy, él mismo médico, farmacéutico y químico. Geoffroy es conocido hoy día por la introducción en 1718 de la Table des differents rapports observés entre differentes substances (Tabla de las diferentes relaciones observadas entre diferentes sustancias). Geoffroy quería una tabla en la que uno pudiese apreciar “de un vistazo” las diferentes relaciones de las “principales materias con las que uno acostumbra a trabajar en química”. La tabla pronto se convirtió no sólo en una colección de información sino también en una herramienta para predecir sales y sus reacciones químicas.

La forma de interpretar la tabla es muy simple:

a) en la fila superior encontramos diferentes sustancias usadas habitualmente en la química del siglo XVII

b) debajo de cada una de estas sustancias se ordenan otras en función de la afinidad que tengan con la sustancia de arriba. Por ejemplo, tomando la primera columna de la izquierda, vemos que está encabezada por los espíritus ácidos, a los que sigue la sal alcalina fijada, la sal alcalina volátil, la tierra absorbente y las sustancias metálicas. Esta columna refleja que la sal alcalina fijada reacciona más favorablemente con los espíritus ácidos que las otras sustancias que están por debajo de ella en la columna y que desplaza a todas las sustancias por debajo de ella de la combinación que tengan con los espíritus ácidos. Así, la primera columna nos dice que la sal alcalina volátil desplaza a la tierra absorbente y a las sustancias metálicas de sus combinaciones con los espíritus ácidos pero que no desplaza a la sal alcalina fijada de las suyas.

c) Geoffroy establece un orden entre las sustancias basándose en la reactividad con la sustancia que encabeza la columna. Pero también establece la importancia del contexto químico o, mejor aún para lo que sigue, el relacional. Por ejemplo, en la segunda columna encabezada por el ácido de la sal marina, la plata reacciona más favorablemente con el ácido en cuestión que el mercurio. Este comportamiento contrasta con el que exhibe en otro contexto, como el de la tercera columna, la del ácido nítrico, donde el orden se invierte y el mercurio reacciona más favorablemente que la plata.

Si bien la tabla planteaba ciertos problemas a la hora de explicar algunos experimentos químicos constituye uno de los primeros intentos de usar pautas químicas para hacer predicciones. Un intento que tuvo sus seguidores (véase La visualización del cambio químico – las tablas de afinidades del siglo XVIII).

¿Y el pensamiento matemático?

Hermann Weyl publicó en 1940 [footnote]Weyl, H.: 1940, ‘The mathematical way of thinking’, Science, 92, 437-46. [/footnote] un artículo en Science titulado “La forma matemática de pensar”. En él, el influyente matemático y físico alemán, siguiendo los pasos de Felix Klein en el programa de Erlangen de 1872, afirmaba que el pensamiento matemático tiene que seguir el pensamiento funcional, es decir, “pensar en términos de variables y funciones”, lo que consiste en tres pasos:

1 Dejar claro el conjunto de variables que se van a considerar

2 Representar las variables por símbolos

3 Construir funciones que relacionen una variable con otra.

En matemáticas, una variable es un “valor”, representado por un símbolo, que puede cambiar, no necesariamente con el tiempo, sino con el contexto en el que se usa la variable. Por otra parte una función es la relación que asigna a cada elemento de un conjunto un único elemento de un segundo conjunto, si bien ambos conjuntos pueden ser el mismo.

No es difícil ver que la tabla de afinidades de Geoffroy constituye una expresión del pensamiento matemático según Weyl. Efectivamente, no tenemos más que considerar lo siguiente:

1 Variables: el conjunto de las sustancias químicas usadas habitualmente en el siglo XVII

2 Símbolos: los que aparecen en la tabla

3 Funciones: las relaciones de orden que se establecen en cada columna.

Este ejemplo ilustra además otro hecho: cómo la matemática discreta, si bien subrepticiamente, llega a la química mucho antes de que lo haga la continua, que lo hará en el siglo XIX de mano de la termodinámica y la cinética.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Esta anotación es una participación de Experientia docet en la Edición 4.1231056 del Carnaval de Matemáticas que acoge Scientia y en la XXVIII Edición del Carnaval de Química que organiza Flagellum