El juego de Penney: tirando monedas con curioso resultado
¿Os gustan los juegos? A quién no le gustan los juegos, ¿verdad? Juegos de niños, juegos de cartas, juegos de preguntas… Cada uno de nosotros tiene su tipo favorito de juegos, y su juego preferido.
Y a todos nos gusta ganar. Sí, eso de «lo importante es participar» está muy bien, pero todos queremos ganar, a todos nos llena más si conseguimos batir a nuestro contrincante. Pero no siempre se puede, unas veces se gana y otras se pierde, aunque lo que sí podemos hacer es intentar buscar la manera de tener mayor probabilidad de ganar que el contrario.
De todos los juegos que podamos recordar, el «Pares o Nones» es el típico juego que se suele utilizar para establecer un orden generalmente relacionado con otro juego: quién empieza a jugar, quién elige primero, quién hace la primera pregunta… La razón es que «Pares o Nones» es un juego justo, ambos jugadores tienen la misma probabilidad de ganar (partiendo de que la elección de los dedos a sacar es puramente aleatoria, como así se puede suponer). Como cuando tiramos una moneda al aire y miramos si salió cara o cruz.
Monedas… Usadas desde siempre como ejemplo de equiprobabilidad. Si tiramos una moneda al aire, la probabilidad de que salga cara (C) es 0.5 y la de que salga cruz (X) también; si la tiramos dos veces, las probabilidades de CC, CX, XC y CC son todas igual a 0,25; si la tiramos tres veces, es igual de probable, 0,125, que salga cualquiera de los siguientes resultado: CCC, CCX, CXC, XCC, CXX; XCX, XXC y XXX; y así sucesivamente.
Vamos a conocer y analizar el siguiente juego con monedas:
El juego enfrenta a dos jugadores y consiste en lo siguiente: cada uno de ellos elegirá uno de los ocho posibles resultados que se pueden presentar al tirar tres monedas (los que hemos escrito antes: CCC, CCX, CXC, XCC, CXX; XCX, XXC y XXX), y después se realizan tiradas sucesivas de una moneda. Gana el jugador cuya elección salga primero.
Vamos a ver un ejemplo. Imaginemos que el jugador A elige CCX y el jugador B elige CXC, y que en las sucesivas tiradas sale CXXCCCX. Entonces ganaría el jugador A, ya que ha salido su jugada (CCX) y la de B todavía no ha aparecido.
Comprendido ya el mecanismo del juego, es interesante analizarlo para ver si nos interesa elegir alguna jugada más que otras. En principio no lo parece, ya que los ocho resultados tienen la misma probabilidad de salir, ¿no? Sí, cierto, pero en lo que respecta a este juego la elección de las ternas es fundamental para tener mayor probabilidad de alzarse con la victoria. Veamos un ejemplo:
Supongamos que el jugador A elige CCC y el B elige XCC. En el momento en el que salga una X ya no podrá ganar CCC, porque cuando aparezcan dos C seguidas ya habrá ganado XCC. Por tanto, la única opción para que gane CCC es que aparezca al principio, y la probabilidad de que eso ocurra es 1/8. Por tanto, con esta elección la probabilidad de que gane A es 1/8 y la de que gane B es 7/8 (el resto).
Bien, ya hemos visto que no todas las ternas tienen la misma probabilidad de ganar, por lo que habrá algunas mejores que otras. ¿Cuál es la mejor? ¿Esta XCC? ¿Alguna otra? Bueno, quizás sería más acertado plantear la pregunta así: ¿Hay alguna terna mejor que todas las demás?
La respuesta, sorprendentemente, es no: no hay ninguna terna que gane al resto. Dada una terna cualquiera, siempre se puede elegir otra con la cual tendremos más posibilidades de ganar que con la primera. Esto quiere decir que el juego es no transitivo (como ocurre en muchas situaciones de nuestra vida).
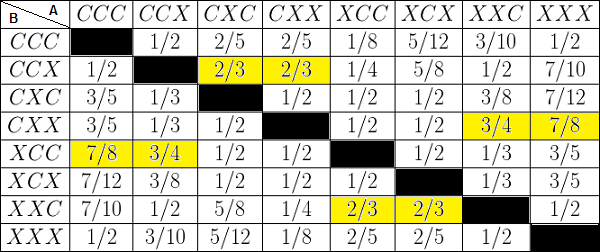
Recordemos que un juego de este tipo es transitivo si cuando A gana a B y B gana a C, entonces A gana a C. Esta propiedad es la que no se cumple en este caso. Sabiendo la elección de A, el jugador B podrá elegir una terna con la que tendrá mayor probabilidad de ganar. En la siguiente tabla se pueden ver las probabilidades de ganar del jugador B a partir de la elección de A. Por tanto, cuando sepamos qué ha escogido A simplemente habrá que localizar esa elección en la fila superior y elegir en esa columna la terna con mayor probabilidad:
Por ejemplo, si A escoge CXX, a B le interesa elegir CCX, ya que tendrá probabilidad 2/3 de ganar. Si en la siguiente partida A escoge CCX, eligiendo XCC el jugador B ganará con probabilidad 3/4.Y así con todas: con cualquier elección inicial habrá otra que será mejor en el sentido de la probabilidad de ganar.
Hay varias maneras de recordar qué terna hay que elegir sabiendo la que ha escogido el primer jugador. Posiblemente la más sencilla sea la siguiente: se toma como primer símbolo el contrario al segundo símbolo de A, y como segundo y tercero el primero y el segundo de A. Por eso para, por ejemplo, la elección XCX de A el jugador B debe escoger X (opuesto de C, el segundo símbolo de la elección del primer jugador) como primer símbolo y XC (los dos primeros de la elección de A) como segundo y tercer símbolo, quedando XXC, que como se puede ver en la tabla es la mejor elección de B.
El origen de este juego se sitúa en 1969, año en el que apareció publicado como problema en el Journal of Recreational Mathematics. El autor fue el matemático Walter Penney. Más tarde apareció en la columna que Martin Gardner tenía en Scientific American en el año 1974. En esta columna aparecían también comentarios sobre el estudio de este problema para elecciones de cuatro resultados (CCCX, XCXC, etc), cuestión que aquí dejamos para el lector. Lo que también aparecía, y que sí vamos a comentar, es un algoritmo para calcular las probabilidades de cada tabla para el caso general, es decir, para elecciones de n resultados. Dicho algoritmo fue diseñado por John Horton Conway y, como no podía ser de otra forma, es para dejar a cualquiera con la boca abierta.
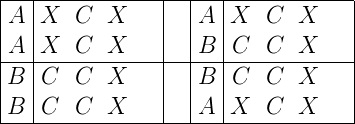
Vamos a ilustrar el algoritmo con un ejemplo de los que acabamos de analizar: vamos a ver qué opciones de ganar tienen A y B si A elige XCX y B elige CCX. Para ello comenzamos escribiendo la de A encima de la de A, la de A encima de la de B, la de B encima de la de B y la de B encima de la de A tal y como muestra la siguiente imagen:
Ahora, para cada pareja calculamos un número en binario de la siguiente forma:
Para cada símbolo de la terna superior, si la lista de k símbolos desde ése en adelante coincide con los k primeros del número inferior escribimos un 1, y si no es así escribimos un cero.
Y después lo pasamos a decimal, teniendo en cuenta que este número en binario está expresando en orden decreciente de potencias de 2 de izquierda a derecha (es decir, el dígito de la izquierda es el que corresponde con el coeficiente de la potencia de 2 más grande).
Vamos a analizar qué número quedaría para AA. Comenzamos con el primero símbolo, es claro que XCX coincide con los tres primeros símbolos que tiene debajo, por lo que encima de la primera X pondremos un 1. Desde el segundo símbolo tenemos que CX no coincide con los dos primeros de la lista inferior (que son XC), por lo que debemos poner un 0. Y desde el tercero tenemos que X sí coincide con el primero de abajo, por lo que pondremos un 1. Queda el número binario 101, que en decimal es 1·4+0·2+1·1=5.
Realizamos el proceso completo obtenemos los siguientes números:
Para calcular ahora las opciones de ganar de cada uno de los jugadores simplemente hay que tener en cuenta que las opciones de ganar se reparten de la forma (AA-AB) a (BB-BA) en favor de B. En nuestro caso, AA-AB=5-0=5 y BB-BA=4-1=3, por lo que la cosa queda 5 a 3 para B. Es decir, que la probabilidad de que gane B es 5/8 y la de que gane A es 3/8, como se puede ver en la tabla. Podéis probar con otras opciones y veréis que este curiosísimo algoritmo funciona a la perfección.
Repito: este algoritmo vale para cualquier longitud de símbolos de las elecciones de cada jugador. Tremendo.
¿A qué esperáis para plantear el juego a vuestros amigos y familiares? Contadnos qué tal os ha ido.
Fuentes y más información:
- Viajes por el tiempo y otras perplejidades matemáticas, de Martin Gardner.
- Un Penney por tu jugada en DivulgaMAT.
- Coin Flip Game Simulation, web donde podrás jugar a este juego con elecciones de cuatro resultados.
Si te ha interesado esta anotación, puedes apoyar su difusión votando aquí.
——————————————————————————————————–
Este post ha sido realizado por Miguel Ángel Morales (@Gaussianos ) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Esta anotación participa en la Edición 4.12310 del Carnaval de Matemáticas, que en esta ocasión organiza Rafael desde Geometría Dinámica.
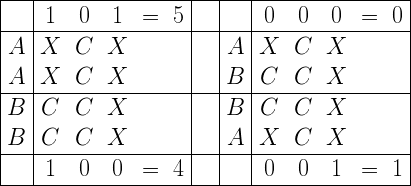
En Zientzia Cultura: El juego de Penney: tirando monedas con curioso resultado – Gaussianos | Gaussianos
[…] leyendo El juego de Penney: tirando monedas con curioso resultado en Cuaderno de Cultura […]
Adds-odds
En realidad tiene toda la lógica del mundo, se trata de dominar la mano del oponente una vez la conoces. Aunque es cierto que no hay una mejor terna en términos absolutos, si te toca elegir primero lo mejor es cualquier terna que no repita en las 2 primeras posiciones (por ejemplo CXC), obviamente. Así hay más mezclas posibles y al menos sólo te ganarán 2/3 veces. No creo que a nadie se le ocurriese elegir CCC si le toca jugar primero.
El concepto de la dominación es recurrente en este tipo de juegos, también aparece en el poker, el dominó o el ajedrez.
¿Es "Pares o Nones" un juego justo en Los Simpson? – Gaussianos | Gaussianos
[…] Y es el más usado para ello por no necesitar de ningún instrumento y, como comentábamos en el post del juego de Penney (y al principio de este párrafo), es un juego justo, ya que la probabilidad de sacar un número […]
Geometría Dinámica » Resumen del Carnaval de Matemáticas 4.12310
[…] El juego de Penney: tirando monedas con curioso resultado (Cuaderno de Cultura científica) […]
Un juego de dados no transitivo — Cuaderno de Cultura Científica
[…] de falta de transitividad se dan, por ejemplo, en el juego de piedra, papel o tijeras, en el juego de Penney o en la situación de ausencia de ganador en la paradoja del voto de Condorcet, por citar […]