Tenemos tres dados de seis caras cada uno de ellos y con sus caras completamente blancas. Disponemos también de dieciocho pegatinas (para pegar en las dieciocho caras que suman esos tres dados) en las que aparecen los números 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 y 18.

Antonio y Beatriz deciden jugar con esos tres dados del siguiente modo:

1. Antonio coloca (como él decida) las 18 pegatinas en cada uno de los lados de los tres dados (una pegatina por lado),
2. Beatriz elige uno de los tres dados (decide cual prefiere mirando la numeración de cada dado),
3. Antonio escoge uno entre los dos dados restantes, y
4. Antonio y Beatriz lanzan su dado.

Gana el juego quien obtiene el número más grande en la tirada.

Imaginemos, por ejemplo, que Antonio rellena un dado con las pegatinas 1, 2, 3, 4, 5 y 6, otro con las pegatinas 7, 8, 9, 10, 11 y 12 y el tercero con las pegatinas 13, 14, 15, 16, 17 y 18. Beatriz estará entonces segura de que va a ganar. ¿Por qué? Basta con que elija el tercer dado (cuyos lados contienen los números más grandes). Da lo mismo que dado seleccione Antonio después, porque obviamente la tirada de Beatriz ganará a la suya. Este ejemplo parece sugerir que elegir en primer lugar es una ventaja para Beatriz, es decir, que la probabilidad de que Beatriz gane es siempre mayor que ½.

Una estrategia ganadora para Antonio

Pero la anterior afirmación no es cierta. Antonio puede colocar las pegatinas de manera que, independientemente del dado que elija Beatriz, él tenga ventaja sobre ella, es decir, él tenga una probabilidad de ganar mayor que ½.

En el artículo de la referencia, Jean-Paul Delahaye sugiere una manera de actuar para que Antonio tenga más probabilidades que Beatriz de ganar.

Esta estrategia (ganadora) precisa que Antonio coloque las pegatinas del siguiente modo:

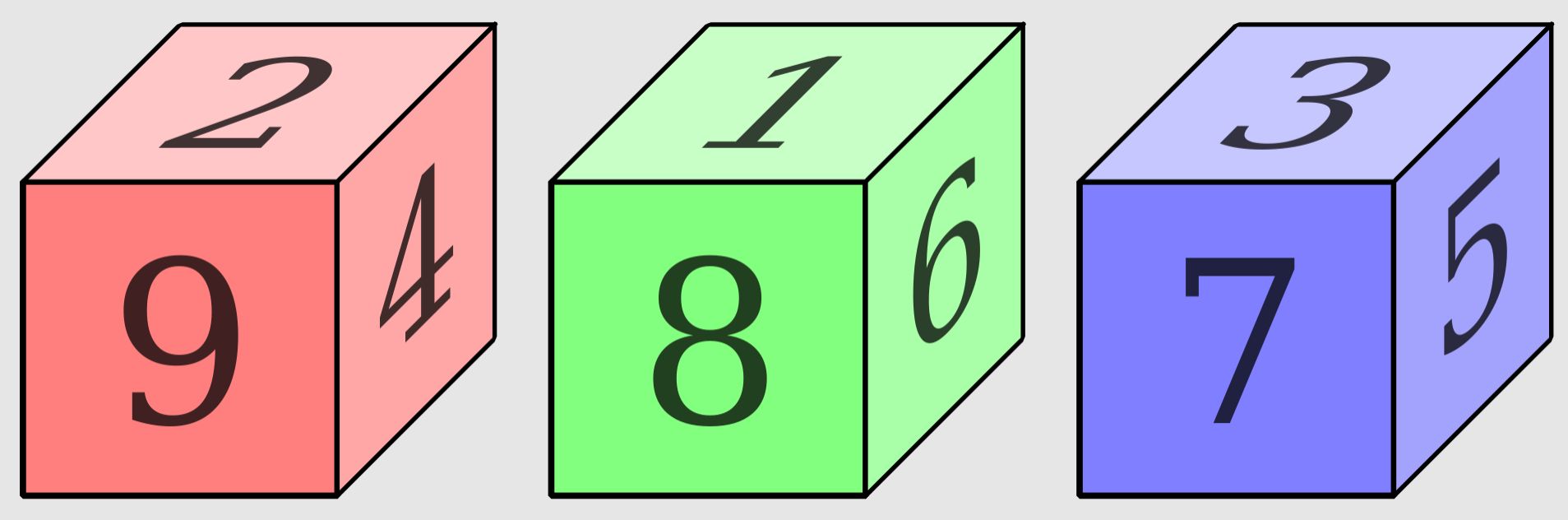
1. en el dado 1 coloca los números 18, 10, 9, 8, 7 y 5,
2. en el dado 2 pega los números 17, 16, 15, 4, 3 y 2,
3. y en el dado 3 coloca las pegatinas restantes con los números 14, 13, 12, 11, 6 y 1.

La tabla de debajo muestra que se da una sorprendente situación cíclica al enfrentar los dados por parejas:

1. el dado 1 gana en 21 tiradas (de las 36 posibles) al dado 2,
2. el dado 2 gana en 21 tiradas (de las 36 posibles) al dado 3, y
3. el dado 3 gana en 21 tiradas (de las 36 posibles) al dado 1.

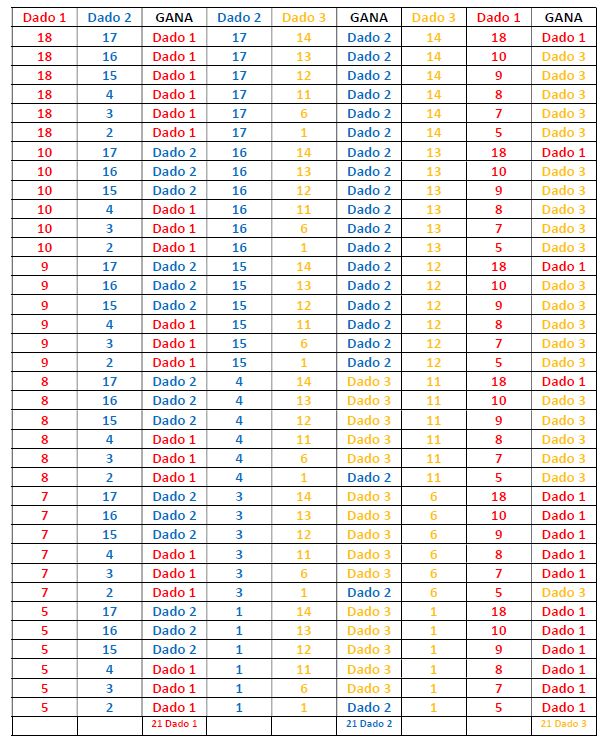
Este fenómeno “paradójico” se debe a la falta de transitividad de este juego. La falta de transitividad alude al hecho de que A gane a B y que B gane a C no implica que A gane a C.

Con esta elección en la numeración de los tres dados, Antonio tendrá siempre mayor probabilidad de ganar que Beatriz. Es suficiente con que siga la siguiente estrategia:

1. si Beatriz elige el dado 1, Antonio deberá escoger el 3,
2. si Beatriz elige el dado 2, Antonio optará por seleccionar el 1, y
3. si Beatriz elige el dado 3, Antonio se quedará con el 2.

De este modo, según lo dicho anteriormente, Antonio tiene siempre una probabilidad de ganar de 21/36; es decir, tiene una probabilidad de ganar en el 58,3 % de los casos.

Bonus

Jean-Paul Delahaye comenta en su artículo otra situación paradójica. Si los tres dados se lanzan simultáneamente, sabemos que hay 216 resultados posibles y equiprobables. Se puede ver que el dado 2 tiene una probabilidad de ganar mayor que los otros dos. Efectivamente, ese dado gana en 90 de los 216 casos posibles, el dado 1 en 63 de los 216 y el dado 3 también en 63 de las 216 posibles tiradas. La equivalencia de los tres dados al enfrentarse dos a dos desaparece cuando se lanzan los tres al mismo tiempo. ¡Una de tantas sorpresas que nos proporcionan las probabilidades!

Nota

Otras situaciones de falta de transitividad se dan, por ejemplo, en el juego de piedra, papel o tijeras, en el juego de Penney o en la situación de ausencia de ganador en la paradoja del voto de Condorcet, por citar algunas.

Referencia

Jean-Paul Delahaye, Le dé le plus fort, Accromath 18, été-automne 2023

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad