Sabemos por las notas y la correspondencia, publicadas póstumamente, de Carl Friedrich Gauss que éste precedió a János Bolyai y a Nikolái Ivánovich Lobachevsky en el desarrollo de la geometría hiperbólica allá por la década de los veinte del siglo XIX y que llegó al convencimiento de que era lógicamente factible que el propio espacio físico fuese hiperbólico, o no euclídeo.

El descubrimiento de las geometrías no euclidianas, parafraseando a Hilary Putnam, es el descubrimiento más importante en la historia de la ciencia para alguien interesado en el estudio de nuestra capacidad de conocer el universo. Efectivamente, privó a los racionalistas de la existencia del conocimiento sintético a priori y dio a los empiricistas una estupenda pista de cómo el conocimiento matemático podría encontrar acomodo en el empiricismo. Veámoslo someramente.

A principios del siglo XIX todo el mundo daba por sentado que la geometría (euclídea) era un conocimiento a priori y una descripción verdadera de la estructura del espacio. Curiosamente quien más heterodoxo se había mostrado con esta idea, aunque en su tiempo no se expresase de esa manera, fue Leibniz, habitualmente etiquetado como racionalista, que, a diferencia de Newton, no consideraba el espacio como un absoluto dado, sino como las relaciones entre los objetos. A diferencia de las verdades a posteriori, las verdades de la geometría euclidiana parecían prácticamente irrefutables, lo que ponía la posición de los empiricistas en serias dificultades.

De igual forma que hizo falta un Einstein para encontrar una forma de comprobar experimentalmente la existencia de los átomos más allá de toda duda razonable en la forma de sus ecuaciones para el movimiento browniano, fue necesario un Gauss para encontrar que si se combinaban las afirmaciones de Euclides con los conocimientos de óptica, se obtenía una conclusión comprobable experimentalmente sobre la geometría del espacio real. Algo así:

Euclides: Los ángulos de cualquier triángulo suman 180º

Óptica geométrica: La luz viaja en líneas rectas

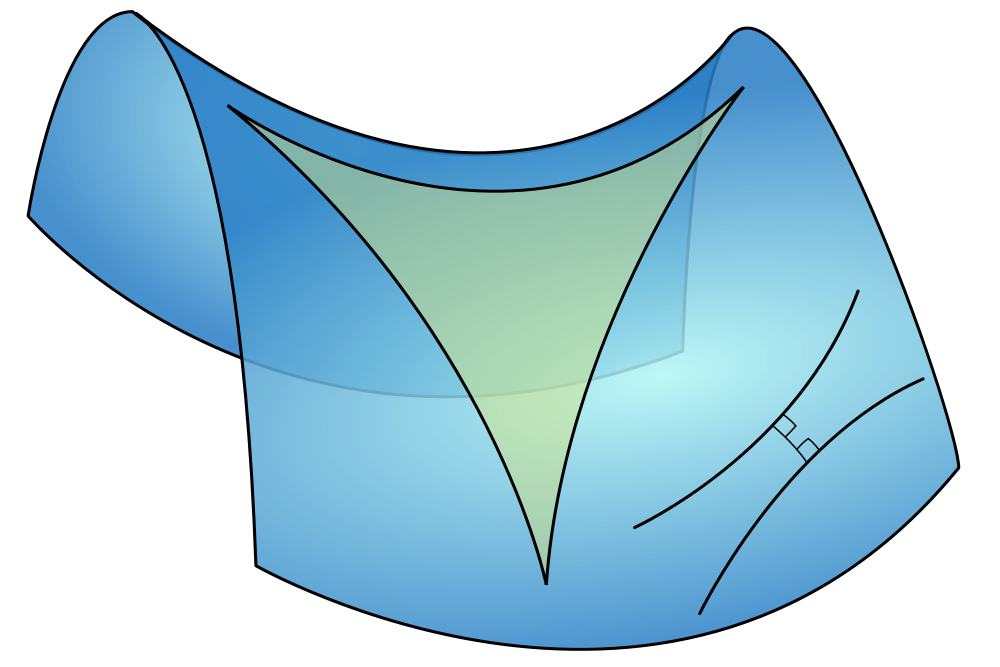
Conclusión: Los ángulos de cualquier “triángulo de luz” (un triángulo cuyos lados sean rayos de luz) suman 180º

Hasta Gauss (o, para el público en general, hasta Bolyai y Lobachevsky) si las mediciones de un triángulo de luz hubiesen contradicho esta conclusión, automáticamente se hubiese achacado a un defecto en la medida, por mucha precisión que ésta pudiese haber tenido, ya que lo contrario nos habría dejado sin una geometría alternativa. La invención [no descubrimiento, que eso es de platónicos] de las geometrías no euclídeas cambió esta situación.

Gauss inventó el heliotropo en 1821. En The Gentleman’s Magazine en 1822 apareció la narración de cómo Gauss había usado su instrumento para medir los ángulos de triángulos de luz para usos puramente geodésicos. Se cuenta que su intención última era medir la geometría real del espacio, asumiendo implícitamente, tendríamos que añadir hoy, que espacio y tiempo existen a priori y son independientes entre sí. Para ello midió los ángulos de un triángulo de luz cuyos vértices correspondían con tres antorchas en las cimas de tres colinas cercanas a Gotinga (Inselsberg, Brocken y Hoher Hagen). Su idea era determinar si la geometría era euclídea o hiperbólica.

Si lo anterior fue exactamente como lo contamos, eso significaría que Gauss fue el primero en darse cuenta de que una vez que se dispone de geometrías alternativas que dan resultados diferentes a la suma de los ángulos de un triángulo de luz, ya depende del experimento determinar qué es “verdad”. Es decir, el conocimiento de la geometría euclidiana deja de ser automáticamente un conocimiento cierto a priori (de hecho nunca lo supimos: la ilusión de que sí nos la dio la pobreza de las matemáticas existentes hasta ese momento). Existe pues una forma de refutar a Euclides: si Gauss hubiese encontrado que la suma era menor que 180º, habría podido afirmar tras las comprobaciones pertinentes que la geometría de Euclides no aplicaba al mundo real, que era hiperbólico (ni que decir tiene que si hubiese medido más de 180º se habría encontrado con un problema, ya que la geometría de Riemann aún no había sido inventada).

La cuestión es que Gauss midió 180º. ¿Probaba esto que la geometría del espacio era euclidiana? En absoluto. Tal y como apuntamos en Provisional y perfectible e ilustramos con Desviación de la luz y falsabilidad, ya no era posible: podía ocurrir perfectamente que los ángulos del próximo triángulo que midiese no sumase 180º. ¿Refutaba entonces el resultado las geometrías no euclidianas? Tampoco. Cada medida realizada tiene un margen de error, por lo que lo máximo que Gauss podía decir era que el triángulo medido poseía unos ángulos cuya suma era 180º más/menos el margen de error. Como la diferencia con los 180º será mayor cuanto mayor sea el triángulo en el caso de las geometrías no euclidianas, siempre se podrá afirmar que como el coeficiente de curvatura del espacio no se conoce, tampoco sabemos lo grande que tiene que ser el triángulo para que las desviaciones de la geometría euclidiana sean apreciables. El conocimiento hasta ese momento cierto, el único sintético a priori, se había convertido en un vulgar a posteriori.

Hoy día, a efectos prácticos en la vida ordinaria y en muchísimas parcelas de la ciencia nos comportamos como si la estructura del espacio fuese euclídea. Pero no nos confundamos, Kant se equivocó al afirmar que debemos (por lógica) estructurar nuestra percepción en principios euclídeos; tuvo razón al decir que siempre lo haremos. Henri Poincaré dijo, à la Kant, que siempre impondremos una estructura euclidiana a nuestra ciencia por simplicidad: al negarnos a tomar en serio una ciencia complicada que no incorpora la geometría euclidiana, hacemos que esta geometría sea verdadera a priori, no porque lo sea, sino por convención.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance