Una de las características más importantes del conocimiento científico, es que este debe ser reproducible. Es decir, diferentes investigadores en diferentes laboratorios, siguiendo el mismo procedimiento experimental, deben llegar a las mismas conclusiones. Esta es la única forma de validar la verdad científica, signifique lo que signifique este vocablo, como cierta y es la excusa que utilizamos muy a menudo para combatir esas pseudociencias que intentan venderse a golpe de estudio irreproducible pagado con talonario de fabricante de agua con azúcar.

Por supuesto, todo esto es muy fácil de comprender en el caso de investigaciones químicas o médicas, debido al relativo bajo coste en materiales y esfuerzo humano que requiere replicar un experimento en estos campos; pero parece difícil comprender cómo trasladar este requerimiento de reproducibilidad a un campo como la física de partículas, donde la construcción de un acelerador como el LHC ha tenido un coste que supera los 3.000 millones de euros y en el que han participado miles de personas. Por tanto, es razonable preguntarse ¿cómo cumplir el requisito de reproducibilidad de un resultado científico cuando el laboratorio de experimentación es único?

Una primera respuesta es que realmente, aunque sólo exista un acelerador, suele haber más de un detector de partículas y, por tanto, se realizan varios experimentos en paralelo, como en el caso de la recientemente exitosa búsqueda del bosón de Higgs por parte de las colaboraciones ATLAS y CMS. Sin embargo, esto no es suficiente, y para encontrar una respuesta completamente satisfactoria hay que formular y contestar otra pregunta ¿por qué se pide en ciencia el requisito de reproducibilidad? Sencillo, para evitar los sesgos del experimentador.

Todo instrumento científico tiene una incertidumbre que provoca que una única medida nunca pueda ser confiable para extraer resultados suficientemente sólidos. Ejemplos de esta incertidumbre pueden ser el hecho de que una regla común no pueda medir menos de un milímetro o que exista un retardo entre las señales intercambiadas por varios sistemas electrónicos. Precisamente, una incorrecta compensación de esto último fue lo que provocó el famoso escándalo de los neutrinos superlumínicos en el experimento OPERA hace tres años. Por ello, los científicos solemos repetir las medidas experimentales una cantidad de veces cuanto más grande mejor, de manera que estas incertidumbres queden diluidas por el tratamiento estadístico que estos datos deben recibir a posteriori. Sin embargo, esto induce un problema extra y es que la selección de cómo repetir las medidas o de cómo realizar el análisis pueden introducir sesgos debido a que, normalmente, el experimentador sabe qué resultado debería obtener al final del experimento, ya sea guiado por experimentos previos o por su intuición.

Imaginemos, por ejemplo, que un científico está midiendo una propiedad que espera que aumente con el ángulo entre dos objetos. Para repetir las medidas, lo que hace es escoger ángulos progresivamente más grandes, de forma que espera obtener una medida también mayor cada vez. Si se diese la situación de que midiendo un ángulo mayor que el anterior, obtuviese un resultado menor, seguramente desestimaría ese valor pensando que ha cometido algún error o lo repetiría hasta obtener un resultado creciente. De esta manera, el experimentador está introduciendo inconscientemente un sesgo que provoca que su resultado no sea estadísticamente tan fiable como debería e incluso puede conducir a un resultado equivocado si, por alguna razón, el resultado fuese sutilmente distinto al esperado, algo que precisamente ocurre en física de partículas, pues muchos experimentos pretender medir procesos que no se espera que ocurran, es decir, el experimentador espera que el valor obtenido para su aparición sea cero; pero que podrían existir con un valor muy pequeño pero no nulo, indicando nueva física y por tanto siendo su medición muy sensible a esta clase de sesgos que acabo de describir. Es por este tipo de situaciones que se introdujo en física el análisis ciego.

Cuando hablamos de análisis ciego, solemos referirnos al análisis de doble ciego realizado en farmacología, en el que tanto los pacientes como los investigadores desconocen a qué pacientes se les ha suministrado medicina y a cuales placebos, eliminando de esta manera los sesgos de experimentador que puedan aparecer. Sin embargo, no es muy común conocer que el análisis ciego, que a diferencia del doble ciego sólo deja en la ignorancia al experimentador, se lleva realizando en física durante décadas, desde que en los años 30, F.G. Dunnington lo utilizase en el famoso experimento de la gota de aceite para calcular la relación entre la masa y la carga del electrón midiendo una cierta variable que dependía del ángulo entre dos piezas del montaje experimental, cuyo valor escogía arbitrariamente pidiendo que un compañero lo ajustase a su preferencia. Desde entonces, esta técnica se ha venido refinando progresivamente para adecuarse a las necesidades de los experimentos modernos.

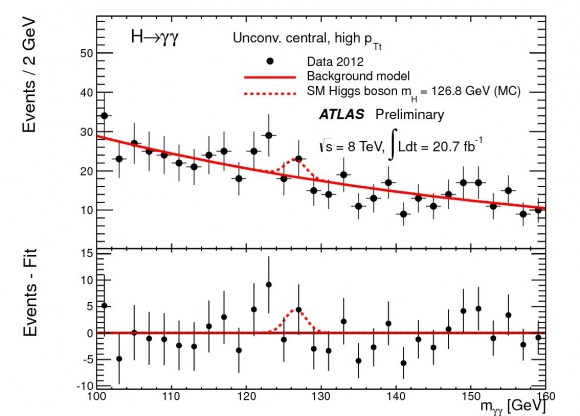
Una implementación moderna del análisis ciego en física de partículas es lo que se conoce como “Señal Oculta”, utilizada frecuentemente en experimentos de búsqueda de partículas en aceleradores. Esta técnica consiste en permitirle al experimentador observar todos los resultados de su análisis estadístico salvo aquellos situados en la región donde se espera observar una señal en caso de que exista. Así, los científicos pueden poner a prueba sus técnicas de análisis observando su efecto en las regiones “a la vista” pero nunca se verán influidos por la consecuencia sobre el potencial resultado del experimento, el cual no observan hasta que deciden que su análisis está listo. Esta es la técnica que se utilizó recientemente en el experimento CDMS, en el que no se supo que existían tres candidatos a partículas de materia oscura hasta que se destapó la señal oculta al final del análisis.

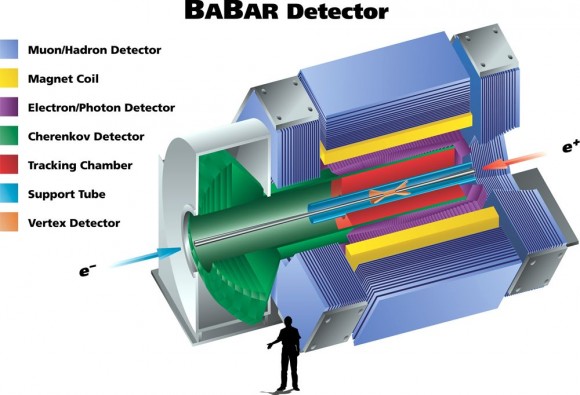
Un paso más en la sofisticación de la eliminación de sesgos es lo que se conoce como “valor oculto” y que se utiliza en aquellos casos en los que el objetivo de un experimento es medir una propiedad, un número concreto relacionado con un fenómeno físico. Por ejemplo, el experimento BABAR está especializado en medir la asimetría CP en las desintegraciones de ciertas partículas llamadas mesones B, cuyo valor esperado es muy cercano a cero y cuyo signo (si es un valor positivo o negativo) se desconoce de antemano. De esta forma, observar el resultado parcial de su análisis de datos podría introducir sesgos debido a la preferencia de un experimentador por un resultado u otro según su no siempre acertada intuición. Sin embargo, la solución no es tan sencilla como ocultar el resultado porque a veces hay que poder observar si el efecto de ciertas partes del análisis es grande o pequeño. Por ello, lo que se hace es, mediante un generador de números aleatorio, multiplicar el resultado por uno o menos uno, de manera que se camufla su signo; además de sumarle un valor constante, con lo que su valor real también se oculta. Ningún investigador tiene acceso a qué constante y por qué signo se ha multiplicado hasta que el análisis de datos se da por finalizado, eliminando así los sesgos posibles a la vez que permitiendo observar los efectos de cada paso intermedio en la implementación del análisis de datos.

Sin embargo, ni siquiera esto es suficiente y conforme los experimentos en física de partículas se han ido sofisticado y complicando, implicando la colaboración de muchos más científicos y buscando señales cada más difíciles de medir, nuevos métodos se han tenido que desarrollar específicamente para cada experimento y tipo de medida, utilizándose conjuntamente con técnicas más generales, como mezclar datos reales con simulaciones de modo que los científicos no saben cuál de los dos están analizando.

Por supuesto, la historia no termina aquí y el futuro, ya sea con la búsqueda de la famosa supersimetría que ya se está llevando a cabo en el LHC o con la construcción de nuevos aceleradores para experimentos cada vez más novedoso; requerirá de una nueva miríada de métodos de aplicación del análisis ciego para impedir que los sesgos estadísticos camuflen resultados cada vez más sutiles en nuestro camino hacia un conocimiento científico cada vez más robusto y completo sobre el comportamiento de nuestro universo. No cabe duda de que la ciencia es apasionante.

Este post ha sido realizado por Mario Herrero-Valea (@Fooly_Cooly) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.