Este texto es una ampliación de la charla divulgativa del mismo título dada por la autora. La charla y el coloquio posterior pueden encontrarse aquí.
Eva Ferreira
Si analizamos el mundo laboral y cómo están representados los grupos de población nos encontramos con diferencias. En particular, si analizamos hombres y mujeres vemos que las mujeres tienen un salario medio menor, en parte debido a que ocupan puestos de menor remuneración que los hombres. Una pregunta natural es ¿Por qué? ¿Cuáles son las razones? ¿Discriminación?, ¿Diferencia en aptitudes?, ¿Diferencias en las preferencias laborales?
Las respuestas nos aportan razones para avalar argumentos a favor y en contra de políticas proactivas para la igualdad laboral entre mujeres y hombres. En resumen tenemos dos tipos de argumentos, que se ponen de manifiesto cuando aparecen propuestas de regulación.
Argumento a favor.- El sistema discrimina a las mujeres, la brecha salarial y la baja representación en puestos altos es consecuencia de ello y por tanto debemos regular para neutralizar esta discriminación.
Argumento en contra.- El mercado laboral es eficiente, se contrata a los mejores, la ley no es discriminatoria y la brecha proviene de diferencias en las preferencias y, como consecuencia, en las elecciones laborales que realizan mujeres y hombres. Regular conllevaría una pérdida de eficiencia.
De forma muy simplificada la idea del argumento a favor es: Si hombres y mujeres son iguales y encontramos diferencias es porque hay discriminación. Y la idea del argumento en contra es: Como no hay impedimentos para que una persona compita por el puesto que quiera, las diferencias que encontramos se deben a comportamientos diferentes entre hombres y mujeres.
En ciertos foros, atribuir las desigualdades a la discriminación o a la tardía incorporación de la mujer en el mercado laboral se entiende como una exageración. En el año 2014 se entiende que las diferencias de oportunidades son muy pequeñas y que, de haber algo de discriminación, tiene un efecto muy reducido. Por ello, el argumento principal que prevalece en contra de la regulación es que la igualdad efectiva es una cuestión de tiempo y que las desigualdades que se mantengan serán reflejo de que somos diferentes.
Vale, me diréis, todo esto ya lo sabemos, pero ¿Qué herramientas nos aportan las matemáticas para pensar en este problema?
El mundo es muy complicado y probablemente las situaciones no sean limpias. Seguramente necesitemos muchas variables para explicar las realidades que encontramos, pero es muy importante ser capaz de encontrar qué efecto neto tiene cada una de las posibles razones.
En esta entrada nos centraremos en el efecto neto de la discriminación. Más que de discriminación, que indica una intención activa en contra, pensemos en un cierto sesgo en contra de las mujeres. Esto significa que como sociedad vemos menos mujeres capacitadas, o las vemos menos capaces, de las que realmente hay. Que hay un cierto sesgo en el sistema no parece estar en discusión. En todo caso, la existencia de un sesgo por género en la sociedad la avalan los resultados de encuestas directas a la población (en Europa el 21% de la población considera que las mujeres no tienen las mismas habilidades que los varones para puestos de responsabilidad, Eurobarómetro 2014), estudios elaborados a partir de experimentos ([1] demuestran cómo universidades de prestigio infravaloran CV femeninos frente a masculinos), o estudios realizados con datos reales que han permitido comparar procesos de selección conociendo el sexo de las personas candidatas y sin conocerlo. Así en [2] los autores muestran que la introducción de audiciones ciegas en los 70 y 80 en las orquestas de USA incrementó en un 50% la probabilidad de que las mujeres candidatas pasaran las rondas de selección
Para entender el efecto neto del sesgo pensemos en una situación muy sencilla, en un mundo donde hay el mismo número de hombres y mujeres, con las mismas habilidades, que se presentan para un determinado tipo de puesto o para formar parte de un equipo de trabajo. Sin sesgo, lo esperado es que la proporción (p) de mujeres elegida sea p=0.5. Por supuesto, esto no sería así en todos los casos, pero sí lo sería en media.
Es decir, el valor esperado de la proporción de mujeres en un determinado proceso de selección con estas características será E(p)=0.5.
Sin embargo, si estamos de acuerdo en que la historia importa y que las cosas no cambian de un día para otro, pongámosle dinámica a este proceso. Así, si t es el tiempo, modelizamos la proporción de mujeres como un valor que va cambiando con el tiempo, de forma que
Es decir, la proporción de mujeres es una combinación de la proporción de mujeres en el pasado () y la proporción de mujeres capacitadas para ocupar ese puesto. Así, si el valor de es muy pequeño, la dinámica de este proceso tendrá mucha inercia (dependerá mucho de su pasado). Por el otro lado, si el valor de es muy grande, habrá poca inercia y la dependencia del pasado es más débil. Esta dinámica refleja el hecho de que los porcentajes de representación por género no cambian drásticamente, bien por esta inercia a la hora de seleccionar nuevas personas, bien por el hecho de que normalmente los cambios son parciales (no se cambian todos los puestos a la vez).
En cualquier caso, si calculamos el límite de este proceso, obtenemos que el valor es
,
siempre que a > 0. Es decir, aunque el proceso tenga mucha inercia, siempre que esta no sea total, efectivamente la igualdad es cuestión de tiempo. Si las condiciones iniciales han sido muy desfavorables a las mujeres, deberán pasar muchos años si el valor de a es muy pequeño, pero el límite es el porcentaje igualitario.
Veamos ahora qué sucede si hay sesgo. Pensemos ahora en que, en términos agregados, seleccionamos un porcentaje menor de mujeres que el que realmente resultaría de la visión anterior. Esto lo modelizamos de forma que
pt = d((1 – a)pt-1 + 0.5a), 0 ≤ d ≤ 1
El valor de d nos indica qué porcentaje de mujeres vemos de entre las que se perciben como candidatas. Si el valor es 1, se perciben todas (ningún sesgo). Si el valor es 0, no se elegirá ninguna mujer (sesgo total). Valores intermedios nos proporcionan situaciones intermedias.
La pregunta ahora es, ¿qué sucederá en el largo plazo?. Hemos visto antes que si no hay sesgo, el efecto de la inercia desaparece en el largo plazo.
¿Qué pasa si, por ejemplo el factor del sesgo es d=0.8?? (Este es un valor alto cercano al uno de la igualdad, que se refleja en una discriminación minoritaria del 20%, ¿acorde quizá con los datos en Europa?)
La intuición nos lleva a hacer el cálculo lineal
Es decir, donde antes llegábamos al 50%, ahora, por culpa del sesgo, llegaremos únicamente al 40%.
Pero lo que sucede es que, cuando hay sesgo, el factor inercia adquiere un papel relevante, incluso en el largo plazo. El valor límite se puede calcular y su expresión es
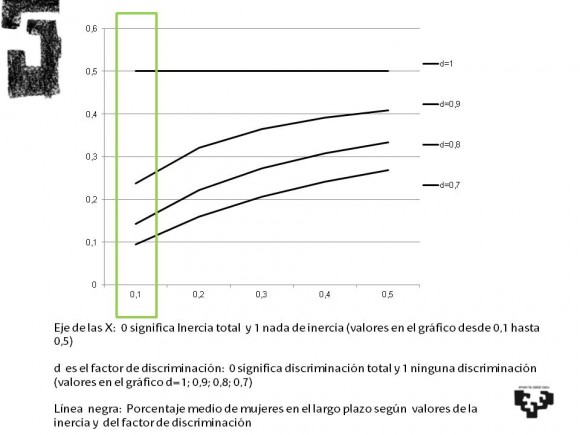
La gráfica muestra cómo el efecto combinado del sesgo y de la inercia es altamente no lineal. Así, si la inercia es grande (recuadro verde, valor de =0.1), incluso con un sesgo moderado de 0.8, la representación femenina no llegaría ni al 15%.
En resumen, el efecto neto del sesgo se ve ampliado de forma drástica cuando hay mucha inercia. Este simple resultado ya nos avisa de que, mientras haya sesgo en la población, la igualdad no sólo no es cuestión de tiempo, sino que su efecto puede ser enorme, mucho mayor de lo que intuitivamente pensaríamos.
Referencias:
[1] Corinne A. Moss-Racusina, John F. Dovidio, Victoria L. Brescoll, Mark J. Grahama, and Jo Handelsmana. “Science faculty’s subtle gender biases favor male students.“Psychological and Cognitive Sciences , 2012.
[2] Goldin, Claudia and Cecilia Rouse. 2000. «Orchestrating Impartiality: The Impact of Blind Auditions on Female Musicians.»American Economic Review 90(4): 715-741
[3] Ferreira, Eva and Espinosa M. Paz (2014) “Glass ceiling effects” Working paper presented in 17th World Congress of the International Economic Association, Jordan 2014
Sobre la autora:
Eva Ferreira es catedrática de economía aplicada y profesora de estadística en la Facultad de Ciencias Económicas y Empresariales de la UPV/EHU


Las matemáticas de la desigualdad | Firm…
[…] Este texto es una ampliación de la charla divulgativa del mismo título dada por la autora. La charla y el coloquio posterior pueden encontrarse aquí. Eva Ferreira Si analizamos el mundo laboral y cómo están representados los grupos de […]
Hitos en la red #23 | Naukas
[…] la de la discriminación por la razón de sexo. Eva Ferreira nos invita a echar unas cuentas en Las matemáticas de la desigualdad. Por cierto, al hablar de esto no es extraño encontrar referencias al comportamiento de los […]