En muchos ambientes es habitual considerar a la estadística como a una hermana pequeña de las matemáticas. Pienso, por ejemplo, en la distinción existente en los programas académicos en la educación secundaria española entre Matemáticas A y B (conocidas por los estudiantes, no sin cierto cachondeo, como matemáticas fáciles y matemáticas difíciles). La principal diferencia es que las conocidas como fáciles incluyen más estadística y menos análisis.

A pesar de este cierto desprestigio social, la estadística, y muy en particular la teoría de la probabilidad, es una rama enormemente rica y sorprendentemente compleja que da lugar a montones de fenómenos que aparentemente contradicen a la intuición.

En el presente artículo me centraré en el concepto de mediocridad, que aparece más o menos escondido en casi cualquier aplicación práctica de la probabilidad, y está en el origen de muchos de los equívocos producidos al intentar interpretarla, además de en un profundísimo concepto de la física.

Las probabilidades se calculan contando

Bueno, contando y dividiendo, pero lo último lo podemos hacer con una calculadora. Al fin y al cabo, probabilidad de un suceso se define como número de casos favorables a ese suceso dividido por el número de casos posibles.

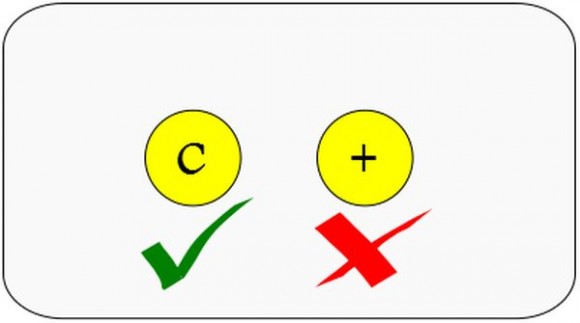
Así, la probabilidad de obtener cara en el lanzamiento de una moneda[1] es de 1 entre 2 (0.5), pues las posibilidades totales son 2 (cara o cruz), de las cuales solamente una es cara. [1] Ninguna de las monedas, dados, etc. del presente artículo estarán trucadas.

Veámoslo gráficamente:

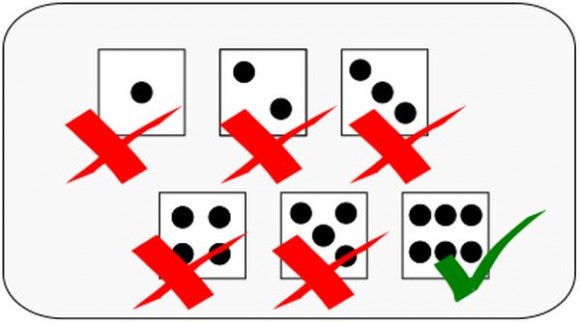
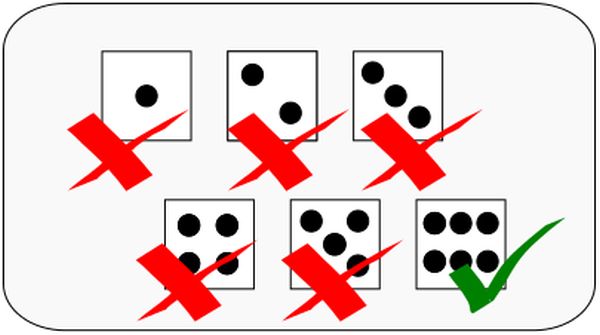
Si ahora queremos calcular la probabilidad de sacar un 6 en el lanzamiento de un dado, podremos usar un diagrama como el siguiente:

De dónde se deduce rápidamente que la probabilidad es de 1/6.

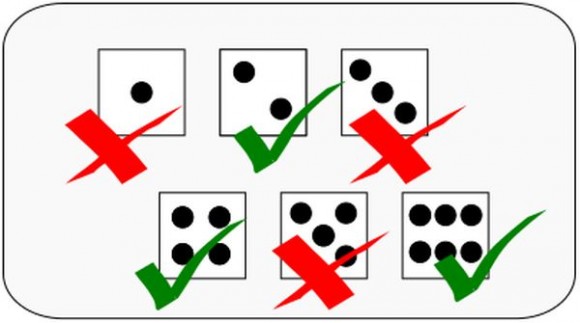
También podemos trabajar con sucesos algo más complicados, como la probabilidad de obtener un número par, en cuyo caso tendríamos:

Siendo la probabilidad en este caso de 3/6, es decir, 0.5.

Contar es fácil, ¿o no?

Queda claro, pues, que para calcular probabilidades basta contar casos posibles, y todos sabemos contar… o eso creemos. Al lector menos cercano a las matemáticas quizá le sorprenda leer que contar no es nada fácil, al menos no siempre. El conteo de casos posibles puede llegar a ser muy dificultoso, existiendo incluso una rama de las matemáticas, la combinatoria, dedicada en exclusiva al arte de contar.

Intente, por ejemplo, contar de cuántas maneras posibles puede sentar a 100 invitados a una boda repartiéndolos en 10 mesas. El problema consiste en contar, pero la respuesta no es obvia.

Pero, ¡alto ahí!, este es un artículo de divulgación… bastante hemos torturado ya al lector en el párrafo anterior. Olvidémonos de casos enrevesados y centrémonos en un problema más básico e importante: ¿cuándo contamos, qué es lo que contamos?

Imagine que le pido que cuente cuántos árboles hay en su calle. ¿Y si ahora le pido que cuente cuántas ramas?, ¿y cuántas hojas? En los tres casos, usted está observando exactamente los mismos objetos, pero los números cambian debido a cómo etiquetamos los conjuntos… a qué es lo que capta nuestro interés en cada caso.

En el fondo es algo bastante obvio, no se puede contar si no se sabe qué quiere uno contar.

Irrumpe la mediocridad: números feos

Con la llegada de las fechas navideñas, muchos de nosotros nos exponemos a un peligro extremo: que nuestros compañeros de trabajo deleguen en nosotros para que escojamos un número para el décimo de lotería de la empresa. Los que, como yo, sabemos de probabilidades, tenemos claro que da exactamente igual qué número escojamos, y que la única certeza es que sea cuál sea habrá compañeros que nos recriminen haber escogido un número tan malo.

Pero, ¿cómo puede un número de lotería ser más o menos malo que otro? Además de las habituales supercherías, es habitual escuchar que los números premiados siempre son números feos. Lo que quieren decir con esto es que rara vez los números premiados son números llamativos (por el motivo que sea) como 00000, 12345 o 31416… a pesar de que los matemáticos, esos listillos, insisten en que son igual de probables que cualquier otro.

Y el motivo es tan sencillo como que, incluso sin aclarar qué significa eso de número feo, hay muchos más números feos que números bonitos. Al igual que cuando agrupábamos ramas en árboles, las probabilidades cambian porque cambia el conjunto que estamos contando. Naturalmente, el fenómeno subyacente es idéntico, y nuestras probabilidades de ganar la lotería jugando a números feos son exactamente las mismas que si jugásemos a cualquier otro.

Este desequilibrio entre casos feos, mediocres, y casos bonitos, especiales, aparece en multitud de fenómenos aleatorios. Y, como veremos, tiene importancia mucho más allá del campo del juego y las apuestas.

La mediocridad crece deprisa: un ejemplo con monedas

Imaginemos que lanzamos varias monedas, y que consideramos que una tirada es bonita cuando todas las monedas dan cara o todas las monedas dan cruz.

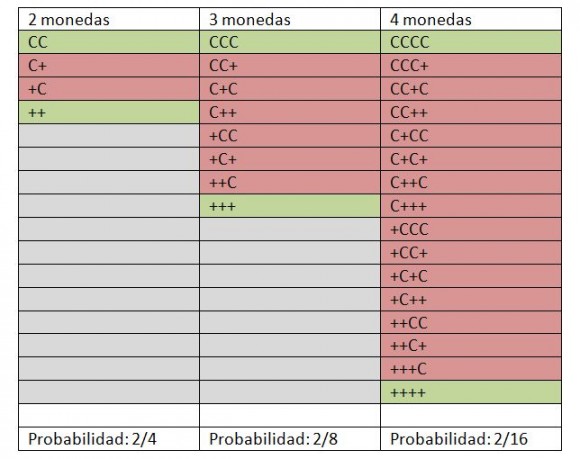
En la siguiente tabla se resumen todas las posibles jugadas para 2, 3 y 4 monedas, marcando en verde las jugadas bonitas:

Como vemos, las jugadas bonitas quedan cada vez más “disueltas” entre una multitud de jugadas feas, mediocres, según aumenta el número de monedas. Cuántas más monedas, más improbable es dar con un estado bonito.

Curiosamente, para la inmensa mayoría de definiciones razonables de lo que es un estado bonito, este comportamiento prevalece.

La mediocridad como “fuerza” física

Existe toda una rama de la física, la mecánica estadística o física estadística, que utiliza constantemente razonamientos semejantes a los que hemos venido desarrollando para obtener conclusiones sorprendentemente exactas.

Sus primeras aplicaciones surgieron en el estudio de los gases.

Un gas se puede interpretar como un conjunto muy numeroso de partículas, cada una con una cierta velocidad y posición que evolucionan en el tiempo, por ejemplo, rebotando entre ellas y con las paredes del recinto que las contiene.

Una sencilla estimación permite establecer que para almacenar las posiciones y velocidades de un mol de partículas (suponiendo 2 bytes por número) se necesitarían del órden de 10¹⁶ Gb de memoria. Esto equivale, groseramente, a 10000 ordenadores por cada ser humano vivo en el mundo. Por no hablar de lo penosa que sería la tarea del encargado de teclear estos datos. En resumen, un enfoque directo es inviable. ¿La solución?, aceptar nuestra ignorancia sobre las posiciones y velocidades y tratarlas como variables aleatorias.

Un ejemplo clásico muy sencillo es el siguiente: la probabilidad de que, dentro de un segundo, todas las partículas de aire de su habitación se concentren en una esquina de la misma es exactamente la misma que la probabilidad de que las partículas se encuentren como están justo ahora (una aquí, otra allá, etcétera etcétera etcétera). También es la misma probabilidad de que “conspiren” todas para apuntar sus velocidades hacia, pongamos, la cabeza del lector, con fatales consecuencias.

¿Debemos temer un golpe de aire asesino?, ¿por qué no nos ahogamos? Simplemente porque las pobres partículas de aire evolucionan entre un amplísimo catálogo de estados mediocres, sin peculiaridades reseñables (ni sustos). Además, al ser tan enorme el número de estados posibles, la probabilidad de salirse de la mediocridad es escasísima.

Mediocridad, fealdad, desorden… o como preferimos decir los físicos: entropía.

Y es que el segundo principio de la termodinámica, tiene mucho, pero mucho que ver con los números feos de la lotería.

Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.