La botella de Klein es un ejemplo de superficie (variedad topológica de dimensión 2) compacta (cerrada y acotada), conexa (de una pieza) y no orientable (contiene bandas de Möbius).

Un precioso resultado sobre superficies compactas y conexas afirma que cualquiera de ellas puede obtenerse como el cociente de una región poligonal en el plano con un número par de aristas identificadas dos a dos (ver [2] páginas 8 a 16). En particular, la botella de Klein es el cociente de un cuadrado cuyos lados están identificados como muestra la figura:

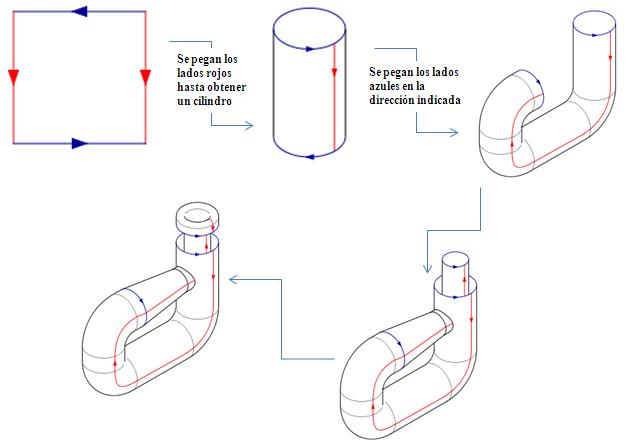
Vamos a ver unas cuantas propiedades de la botella de Klein ayudándonos del cuento Botella de Klein de Juan José Arreola (1918-2001); se reproduce el texto íntegramente y añadimos después algunas notas explicativas.

–oOo–

BOTELLA DE KLEIN

“El cilindro es al toro lo que la Banda de Moebius a la Botella de Klein”⁽¹⁾. Y Francisco Medina Nicolau sacó de una gaveta la célebre cinta de papel, ahora con las puntas pegadas de un modo particular, como en un cuello de camisa. Sus manos de prestidigitador la hicieron girar y en el aire quedó la forma pura:

– Cuando la Banda de Moebius se esconde en ella misma, surge la Botella de Klein… ¿La ves?

Quedé perplejo y salí por tangente literaria:

– Es el procedimiento de Kafka, según la ley de Roberto Wilcock: sacarse de la cabeza un objeto, escamotearlo y seguir hablando sobre él…

El doctor Garfias estaba presente.

– A propósito de cabeza, no se la quiebre usted, que al fin y al cabo la botella es de vidrio. La inventaron los alquimistas. Creo que fue Jehan Brodel, denunciado a la Inquisición por sus vecinos de la calle del Pot de Fer ¿se acuerda usted? El cuerpo infame sin principio ni fin era la imagen blasfematoria de Dios. Fue destruido el original y los dibujos previos también. Pero la cosa llegó si no a los ojos, a los oídos del Bosco⁽²⁾, que pintaba de memoria: allí está el ámpula, la burbuja de jabón que encierra a los amantes en el Jardín de las Delicias…

Ludlow llegó en ese momento con envoltorio sospechoso y sonrisa feliz. Había alcanzado a oír las palabras de Garfias y enlazó los puntos suspensivos:

–… la botella figura también dentro de la tradición castellana. Es el fracaso del Marqués de Villena citado por Quevedo y por Vélez de Guevara. Es la redoma que encerraba al Homúnculo, el feto infernal, el niño que no necesita madre para nacer…

Mis tres doctores en física, topología y lógica⁽³⁾ me acorralaron en una superficie collado sin pies ni cabeza. Hicieron y deshicieron nudos imaginarios y reales con cuerdas y palabras. Yo dije, recordando a Rafael, que el collado se parece al fuste de una silla de montar y que los artesanos de Colima trazan la superficie sobre pergaminos como Dios les da a entender sirviéndose de patrones heredados. Se rieron. Jorge Ludlow desenvolvió su paquete.

– ¿Quería una Botella de Klein?

No paso a creerlo. Siguiendo indicaciones precisas, los diseñadores y obreros de la casa Pyrex⁽⁴⁾, especializada en materiales refractarios, me hicieron el capricho. No paso a creerlo. Después de muchas tentativas, aquí está el milagro físico sin interior ni exterior, perfectamente soplado y sin defecto.

Ahora estoy sólo frente al objeto irracional, llenándolo con mis ojos antes de ponerle tinto de Borgoña. Aquí está sobre mi mesa de ¿trabajo? la Botella de Klein que busqué por más de veinte años de ¿trabajo?

Mi mente trabajada no puede más, siguiendo las curvas del palindroma de cristal. ¿Eres un cisne que se hunde el cuello en el pecho y se atraviesa para abrir el pico por la cola? Me emborracho mentalmente gota a gota con la clepsidra que llueve lentamente sus monosílabos de espacio y tiempo. Mojo la pluma en ese falso tintero y escribo sin mano una por una las definiciones inútiles: signos de interrogación estatuaria. Trompa gigante de Falopio. Corno de caza que me da el toque de atención al silencio, cuerno de la abundancia vacía, cornucopia rebosante de nada… Víscera dura que desdice la vida diciendo soy útero y falo, la boca que dice estas cosas: soy tu yo de narciso inclinado a su lirio, tu dentro y tu fuera, abierto y cerrado, tu liberación y tu cárcel, no bajes los ojos ¡mírame!

Pero ya no puedo mirar porque la cabeza se me fue a las entrañas, ¿porque los topólogos no trabajan con vísceras y desarrollan hígados, riñones y asas intestinales en vez de nudos y toros? Se lo voy a proponer si despierto mañana.

Por ahora empuño la Botella de Klein. La empuñas, pero no la empinas. ¿Cómo puedo beber al revés? Tienes miedo en pie como falso suicida, jugando metafísico el peligroso juguete en tus manos, revólver de vidrio y vaso de veneno… Porque tienes miedo de beberte hasta el fondo, miedo de saber a qué sabe tu muerte, mientras te crece en la boca el sabor, la sal del dormido que reside en la tierra…

–oOo–

NOTAS

(1) El toro (la superficie) se obtiene a partir de un cuadrado haciendo las identificaciones que se indican en la figura 2:

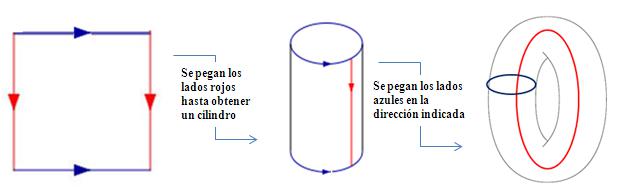
Es decir, el toro se obtiene identificando las dos circunferencias que forman el borde del cilindro de la figura 2. Para construir la botella de Klein, podrían haberse identificado en primer lugar los dos lados marcados en azul (figura 1): se habría obtenido así una banda de Möbius, cuyo borde debería identificarse siguiendo las indicaciones de las flechas rojas. En el video de debajo se explica con gran claridad cómo se obtiene la botella de Klein con el proceso indicado en la figura 1; después se corta por la línea roja (también en topología cortar es el proceso inverso a pegar: se estaría deshaciendo el cilindro obtenido en primer lugar) y se obtiene una banda de Möbius.

(2) Observad el panel central de El Jardín de las Delicias: en el relato se refiere a la zona marcada en el cuadro, el ámpula en la que se sitúan los amantes, ¿una botella de Klein?

(3) Se refiere a Francisco Medina Nicolau (1929-2001) físico mexicano, el Doctor Garfias y Jorge Ludlow, con los que comparte esta ‘reunión científica’.

(4) La botella de Klein no vive en dimensión 3. En la figura 1, y en todas las representaciones de esta superficie, se autointerseca al realizar la identificación. Esta es la prueba de que no puede embeberse (incluirse de manera ‘fiel’) en el espacio en el que vivimos. La botella de Klein vive de manera natural en dimensión 4. Los obreros de la casa Pyrex –aunque no dudo de su profesionalidad– no pueden hacer milagros: el mejor fabricante de botellas de Klein en vidrio que conozco es el físico Cliff Stoll (figura 5) que mantiene la página ACME Klein Bottles; sus magníficas botellas, aunque preciosas, son en realidad una proyección en 3D de esta superficie no orientable.

Botella de Klein encierra numerosas metáforas (ver [3]): el narrador acaba entrando dentro de la botella de Klein, o transformándose en ese objeto, que califica de irracional. Ese retorcido, como el cuello de un cisne, dotaa la botella de Klein de cualidades excepcionales –provienen en realidad de su falta de orientabilidad–: representa al mismo tiempo la perfección absoluta, el mal, la muerte…

Más información:

[1] Juan José Arreola, Palindroma, Joaquín Moritz, 1974

[2] Marta Macho Stadler, Topología Algebraica, Apuntes Máster 2014-2015

[3] Paul Quinn, Arreola, Escher y Barth. Una eterna brida dorada, Actas del XIII Congreso de la Asociación Internacional de Hispanistas (1998), vol III, 356-361

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.