El matemático Frank Harary (1921-2005), uno de los padres de la teoría moderna de grafos, propuso utilizar esta teoría matemática para representar la intriga de obras literarias, en particular las relaciones amorosas contenidas en ellas.

En La teoría de grafos y “Così Fan Tutte” dábamos un ejemplo de esta propuesta de Harary para estructurar y comprender la intriga de la ópera bufa Così fan tutte ossia La scuola degli amanti de Wolfgang Amadeus Mozart.

Esta vez, estudiaremos las relaciones amorosas de la novela A severed head (1961) –Cabeza cortada– de la escritora y filósofa Iris Murdoch (1919-1999). Frank Harary propone este análisis en el artículo [1].

En esta novela satírica se presenta un sexteto amoroso, entre:

1. El protagonista, un comerciante de vino, Martin Lynch-Gibbon,
2. Su amante, Georgie Hands,
3. Su esposa, Antonia,
4. El psicoanalista Palmer Anderson,
5. El hermano del protagonista, el escultor Alexander,
6. La hermanastra de Palmer, la antropóloga Honor Klein.

Empecemos por resumir su argumento:

Martin ama a su esposa y a su amante. Antonia le confiesa que es amante de Palmer, y que se quiere casar con él, aunque sin renunciar del todo a su actual matrimonio. Se forma un trío entre Martin, Antonia y Palmer. Cuando Antonia se entera de la infidelidad de Martin, Georgie se incorpora al trío. Martin se enamora más tarde de Honor: la encuentra en la cama con Palmer, quien decide dejar a Antonia para seguir con su hermana. Georgie conoce a Alexander, y se compromete con él. Pero Alexander está enamorado de Antonia, de quien ha sido amante en secreto durante años. Georgie intenta suicidarse, fracasa y se va a vivir a América con Palmer, mientras que Honor se queda con Martin.

Harary expresa mediante un grafo todos los intercambios de parejas explicados en el anterior resumen. Para ello asigna a cada personaje un vértice del grafo. En la imagen de debajo representamos a las mujeres en rojo –H es Honor, A Antonia y G Georgie– y a los hombres en azul –A es Alexander, M Martin y P Palmer–. Las aristas unen vértices siempre que las personas correspondientes hayan tenido alguna relación amorosa en algún momento. Además, Harary asigna números a cada arista del grafo, para indicar las relaciones de manera temporal –es decir, el orden en el que se van cambiando las parejas, aunque los números no indican que esas relaciones se producen de manera simultánea–. Todas las mujeres se emparejan con todos los hombres en algún momento de la trama, pero no se producen relaciones entre personas del mismo sexo. El grafo representando los juegos amorosos del sexteto es:

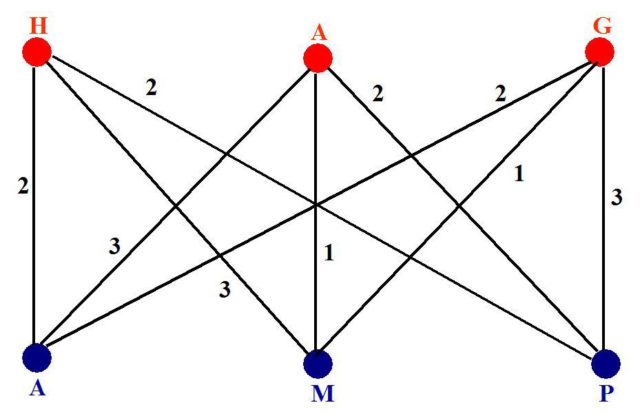
Este grafo es el conocido como K_3,3;recordemos algunas de sus propiedades:

1. K_3,3es un grafo no planar, es decir, no es posible dibujarlo en el plano sin que al menos dos aristas se crucen. Debajo puede verse una representación del grafo K_3,3 con sólo un cruce, que no es posible evitar. Puede verse una prueba de que no es planar en este enlace.

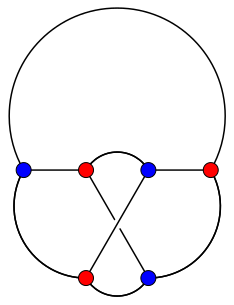
2. K_3,3 es un grafo bipartito, es decir, sus vértices se pueden separar en dos conjuntos disjuntos de manera que las aristas sólo conectan vértices de que no están en el mismo conjunto. En el caso de A severed head, los dos conjuntos disjuntos son los de las mujeres por un lado y los de los hombres por otro, que sólo mantienen relaciones con personas de diferente sexo.
3. K_3,3 es un grafo bipartito completo, porque todos los vértices del primer conjunto aludido en 2. Se pueden relacionar con todos los del segundo: en efecto, todas las mujeres se relacionan con todos los hombres.
4. K_3,3 se llama a veces grafo de utilidad porque aparece en un conocido acertijo matemático… que no tiene solución.

¡Un curioso y especial grafo representando a una también especial obra!

Referencia

[1] Frank Harary, Structural study of “A severed head”, Psychol Rep October vol. 19 no. 2 (1966) 473-474.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Esta entrada participa en la Edición 7.8 del Carnaval de Matemáticas, que en esta ocasión organiza el blog “Que no te aburran las M@tes” de Elisa Benítez Jiménez.