Expansión libre, la reina de los procesos irreversibles

Una de las ideas más iluminadoras que aprendí durante la carrera fue el siguiente ejemplo. Se trata del ejemplo más sencillo que conozco para arrojar algo de luz sobre el concepto de irreversibilidad. A pesar de su sencillez da una idea bastante fidedigna del “sabor” de la mecánica estadística. Para disfrutarlo, en primer lugar, tendremos que hablar sobre la expansión libre de un gas.

Imagine el lector que tenemos dos compartimentos contiguos. En el de la izquierda introducimos un gas, que podemos visualizar como un conjunto de partículas (átomos o moléculas) rebotando contra las paredes. El compartimento de la derecha está vacío. En un momento dado, abrimos la pared que separa ambos compartimentos, permitiendo que el gas se expanda por ambas cavidades.

Si ahora volvemos a cerrar la compuerta, el gas permanecerá repartido en ambas cavidades. Tras abrir y cerrar la puerta, no se regresa al estado inicial. De hecho, esperamos que la presión y la cantidad de moléculas en cada compartimento sea la misma. Estamos ante un proceso irreversible, un proceso que sucede solamente en una dirección y nunca en la contraria.

Sin embargo, lo que tenemos ante nosotros no es más que un grupo de partículas rebotando aquí y allá. ¿Qué es lo que impide a nuestras partículas volver a organizarse en el compartimento izquierdo, aunque solo sea por casualidad? Lo cierto es que no hay nada que lo impida. ¿Por qué no sucede entonces?

Un modelo de juguete

Para continuar, introduciremos un modelo muy sencillo de la expansión de un gas. Tan sencillo que tiene forma de juego de mesa. El tablero tiene el siguiente aspecto:

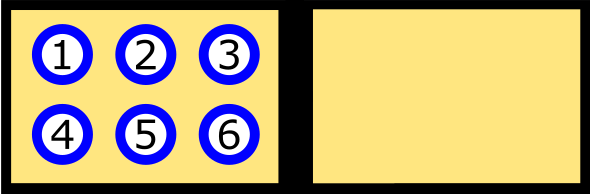
Hemos introducido seis bolas en la mitad izquierda del tablero. Estas bolas representan moléculas de gas, de modo que la configuración que vemos en la figura representa el caso de gas en la cavidad izquierda y vacío en la cavidad derecha.

Ahora necesitamos establecer cuál será la dinámica del juego, esto es, qué reglas seguiremos para actualizar el tablero después de cada “tirada”. Optemos por la sencillez: en cada “tirada” lanzaremos un dado y, si obtenemos, por ejemplo, un dos, la bola número 2 cambiará de compartimento. En la siguiente figura se puede ver una sucesión de varias tiradas.

Es posible que el lector piense, y no le falta razón, que el modelo aquí presentado es demasiado simple. Al fin y al cabo, la humanidad sabe mecánica suficiente como para calcular realmente cómo se han de mover las moléculas, sin recurrir a algo tan poco sofisticado como tirar un dado. El procedimiento clásico sería:

1. Anotar todas las posiciones y velocidades de las partículas involucradas.
2. Usar las leyes de Newton para escribir sus ecuaciones de movimiento.
3. Resolver dichas ecuaciones.

Sin embargo, cuando tratamos con las cantidades colosales de moléculas presentes en una muestra macroscópica de gas, ni siquiera es posible dar paso número uno. No queda más remedio que usar métodos de mecánica estadística, en los que se asume que las posiciones y velocidades son aleatorias. Estas variables aleatorias se toman de distribuciones de probabilidad, lo cual no deja de ser un “dado” algo más sofisticado. En resumen: puede que nuestro juego sea aburrido, pero como modelo no está mal.

Juguemos

Pero volvamos a nuestro sencillo tablero. Tras unas pocas tiradas, tendremos bolas repartidas por ambos lados. El juego consiste en seguir tirando el dado hasta que bolas se vuelvan a ordenar en el compartimento izquierdo. Parece poco probable que suceda, pero no imposible. De hecho, basta con jugar el tiempo suficiente. Concretamente, uno esperaría que por azar las bolas se reordenasen como en la configuración inicial alrededor de una vez por cada 64 tiradas[1].

Lo anterior es cierto para 6 bolas, pero nada nos impide construir un tablero de mayor tamaño. Es fácil ver que un tablero con N bolas posee 2^N configuraciones distintas[2]. En este caso general, uno esperaría regresar al estado inicial tras aproximadamente 2^N tiradas. Con solamente 20 bolas, necesitaríamos más de un millón de tiradas para volver a la configuración inicial siguiendo las reglas del juego. Con 100 bolas, el número de tiradas necesarias es astronómico: un uno seguido de treinta ceros, y eso estimando por lo bajo. En la siguiente animación podemos ver precisamente un caso con 100 casillas[3].

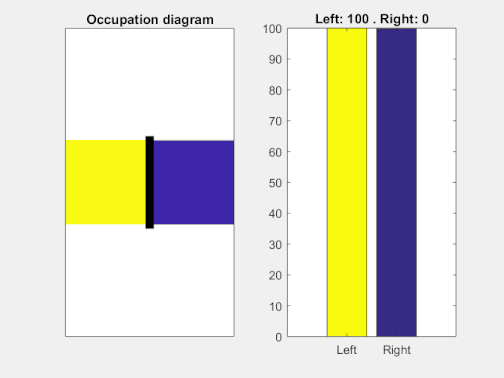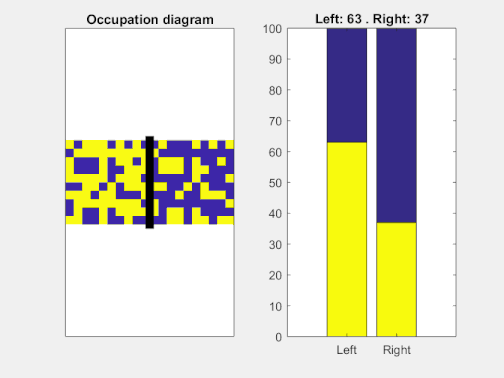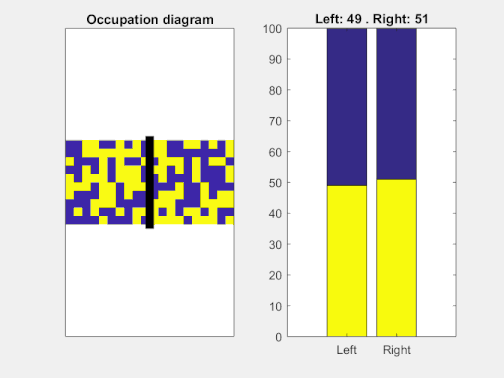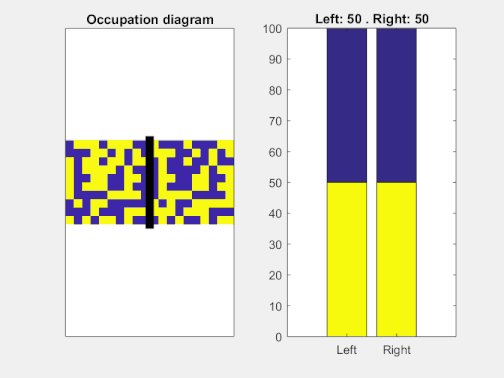
Si representamos los números de partículas en cada una de las dos cavidades en función del tiempo, podemos ver cómo la “expansión” es más rápida y violenta al principio y más lenta cuánto más cerca estamos del equilibrio termodinámico. Nótese cómo incluso con una dinámica tan tonta como repartir las partículas al azar estas tienden a “repartirse” por ambos compartimentos, con pequeñas fluctuaciones.

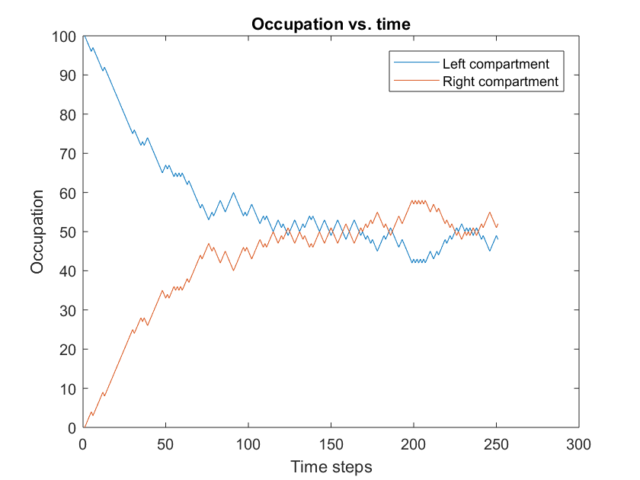
En el caso de un gas, incluso para volúmenes no muy grandes, manejamos cantidades colosales de moléculas, y el número de “tiradas” necesarias para volver al estado inicial, al depender exponencialmente del número de moléculas, ¡crece de un modo más colosal aún! La probabilidad de que haya fluctuaciones menos extremas (por ejemplo, 70% a la izquierda-30% a la derecha) también decrece rapidísimamente con el tamaño del sistema.

En resumidas cuentas: usando una dinámica aleatoria sobre un sistema lo suficientemente grande y prestando atención a la variable adecuada (en este caso, número neto de partículas a cada lado) se obtiene un resultado que, a todos los efectos prácticos, es exacto.

Resumiendo más aún: en ocasiones, azar + inmensidad = ley física.

Bola extra

Me permito la licencia de lanzar una pregunta al lector. En el modelo que hemos mostrado todas las posibles configuraciones del tablero son igualmente probables. ¿Cómo es posible que se pase más “tiempo” en aquellas que reparten equitativamente las partículas por cada compartimento?

Pista aquí.

Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.

Notas y referencias:

[1] Dónde se han ignorado los efectos de forzar de la configuración inicial.

[2] Podemos verlo notando que nuestro tablero se parece mucho a un número binario, dónde 0 representa casilla vacía y 1 representa casilla ocupada. En el ejemplo con 6 bolas hay tantas configuraciones como números binarios entre 000000 (cero, representando todos los compartimentos izquierdos vacíos) y 111111 (sesenta y tres, representando todos llenos), esto es, 64 configuraciones posibles.

[3] El código para generar animaciones como estas está disponible aquí.