La espaguetización es el efecto de las fuerzas de marea gravitacionales sobre un astronauta flotando en el espacio cerca de un agujero negro. Cuando estás de pie en el suelo hay una diferencia entre la aceleración de la gravedad en tu cabeza y en tus pies, pero es tan pequeña que no notas nada. Sin embargo, cerca de un objeto de gran masa, como un agujero negro de masa estelar, la diferencia puede ser grande. Conforme te acerques al agujero negro pasará de ser incómoda a un doloroso potro de tortura medieval que te acabará desmembrando.

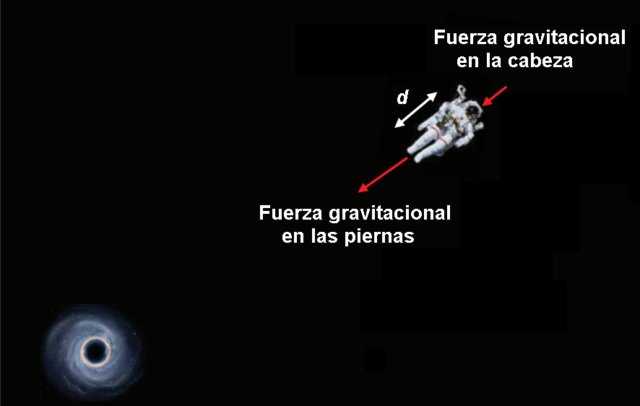
Los agujeros negros son muy pequeños, tanto que son los objetos astrofísicos más compactos que se conciben. Su tamaño viene dado por el radio de Schwarzschild de su horizonte de sucesos, la frontera más allá de la cual ni siquiera la luz puede escapar. Este radio es proporcional a su masa, en concreto, R = 2 G M/c², donde G = 6,67 × 10⁻¹¹ N · m² kg⁻² es la constante de gravitación universal de Newton, c = 3,00 × 10⁸ m/s es la velocidad de la luz en el vacío y M es la masa del agujero negro. La masa de un agujero negro se suele medir en unidades de masa solar (M_☉), luego su radio R = 2,95 (M/M_☉) km. Por ejemplo, un agujero negro de 10 masas solares tendrá un radio de 29,5 km y uno de 100 masas solares un radio de solo 295 km.

Para calcular la diferencia de fuerzas gravitacionales entre la cabeza y los pies de un astronauta hay que usar un modelo de esta persona junto con su traje espacial. Supongamos que mide 1,70 metros de altura con el traje puesto y que su masa es de 150 kilogramos (unos 80 kg para el traje espacial y unos 70 kg para su peso). Para hacer los cálculos más sencillos vamos a suponer que la cabeza con casco y los pies con botas pesan lo mismo, sean m = 20 kg cada uno, no viéndose afectado el resto del cuerpo; además, supondremos que la distancia entre los centros de masa de la cabeza y de los pies es d = 1,50 m. Un cálculo sencillo [1] nos dice que la diferencia de fuerzas entre la cabeza y los pies es ∆F = R m c² d/r³, donde m es la masa común de pies y cabeza, d es la distancia que separa sus centros de masa y r es la distancia que separa el centro de masas del astronauta y el centro del agujero negro.

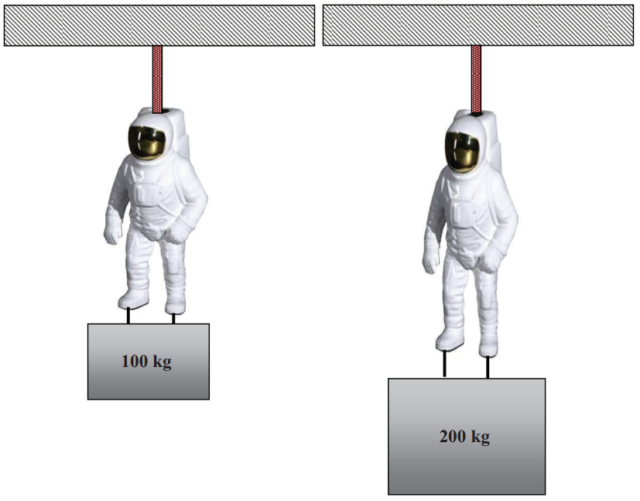
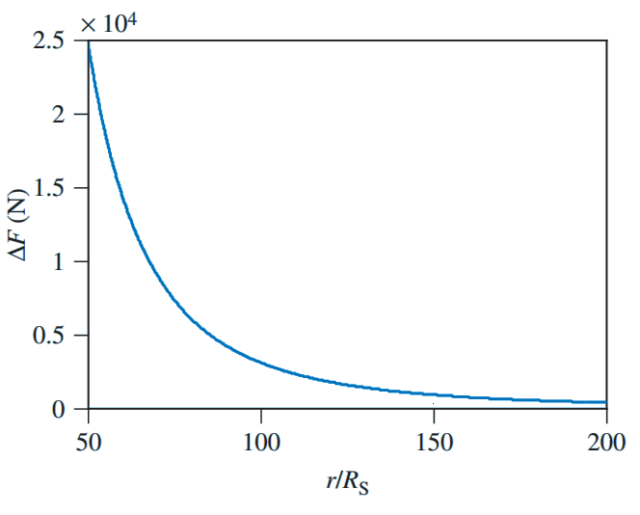
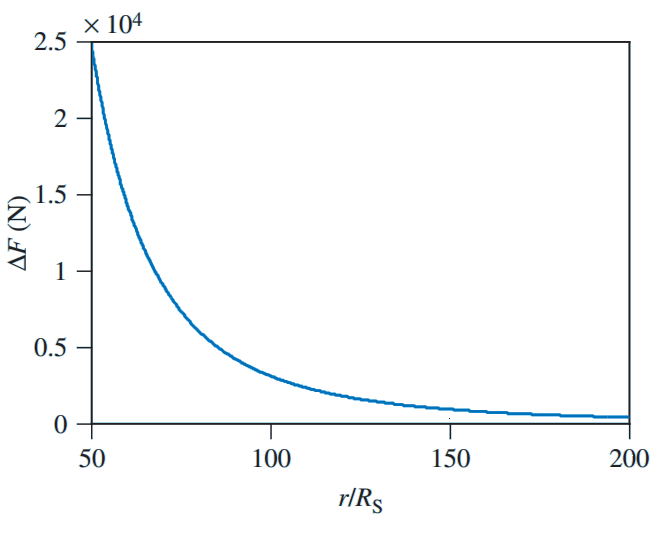
Usando la fórmula anterior puedes hacer los cálculos para cualquier agujero negro que desees. Solo como ejemplo supondré un agujero negro de 10 masas solares y 61 km de diámetro, con lo que ∆F = 3,11 × 10⁹ / (­r/R)³ newtons (N). Para un astronauta a una distancia de 200 radios de Schwarzschild, unos 5900 km, se obtiene ∆F = 388 N; esto equivale a soportar unos 40 kg de peso sujeto a los pies de un astronauta que esté colgado por un cable de acero a pocos metros de la superficie terrestre (como ilustra la figura 2). Quizás sea algo incómodo, pero se puede soportar sin problemas.

La distancia más próxima al agujero negro que podrá soportar el astronauta depende de lo que soporte su cuerpo. Pero seguro que estará muy incómodo a una distancia 130 radios de Schwarzschild, unos 3800 km, pues ∆F = 1400 N; esto equivale a soportar unos 140 kg de peso bajo los pies. ¿Cuánto podrá soportar hasta que empiece a desmembrarse? A una distancia de 100 radios de Schwarzschild, unos 3000 km, soportará ∆F = 3100 N, un peso colgante de unos 310 kg tirando de los pies. ¿Podría acercarse a unos 1500 km del agujero negro? No, pues a unos 50 radios de Schwarzschild debería ser capaz de soportar unos 2500 kg de peso colgados de los pies.

Los agujeros negros son objetos muy pequeños y el disco de acreción de materia que les rodea suele tener menos de 10 radios de Schwarzschild de diámetro. El ojo humano tiene una resolución angular mínima de un minuto de arco, o sea, unos 30 cm a 1 km de distancia (0,3 miliradianes). La Luna y el Sol tienen un diámetro aparente en el cielo de unos 9 miliradianes. Para ver el disco de acreción de un agujero negro con un tamaño similar al de la Luna en el cielo hay que acercarse a unos 1100 radios de Schwarzschild; a esa distancia las fuerzas de marea gravitacionales serán tan pequeñas que el astronauta no las notará.

¿Qué pasa con un agujero negro sin disco de acreción? Un agujero negro sin disco de acreción deforma la imagen del fondo estelar a su alrededor gracias a su efecto como lente gravitacional. Para disfrutar de este efecto (muy popular en las representaciones artísticas de los agujeros negros que decoran las noticias sobre las ondas gravitacionales detectadas por LIGO/Virgo) hay que acercarse a unos 220 radios de Schwarzschild. Por fortuna a esa distancia el astronauta sentirá que sus pies le pesan un poco, pero por lo demás estará perfectamente cómodo.

En la divulgación de la Física una fórmula vale más que mil palabras. Te animo a usar la fórmula que decora este texto para realizar cálculos con otros agujeros negros, estrellas de neutrones y cuerpos astrofísicos. Sobre todo si eres profesor de enseñanza secundaria; vamos, anima a tus alumnos a realizar estos cálculos sencillos. La mejor manera de apreciar lo pequeños que son los agujeros negros es calcular cuánto nos podemos acercar a ellos para verlos con el mismo detalle con el que vemos la Luna en el cielo.

Este post ha sido realizado por Francis Villatoro (@Emulenews) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

Referencias

[1] Stylianos V. Kontomaris, Anna Malamou, “A presentation of the black hole stretching effect,” Physics Education 53: 015010 (2018), doi: 10.1088/1361-6552/aa8d22.