Si uno le pregunta a Google Images qué es un una gráfica, puede encontrarse con un esperpento como el siguiente:

Más allá de la fealdad generalizada y los colores estridentes, la web y los medios de comunicación están plagados de ejemplos de malas representaciones de datos. Ejemplos donde el artificio y la ornamentación pervierten la función de estas poderosas herramientas.

¿Qué es una gráfica entonces? Dado que Google no parece ser de gran ayuda en este caso, yo os propongo la siguiente definición: una gráfica es una representación de datos numéricos mediante recursos visuales que permite interpretarlos y extraer información de ellos. Las gráficas son herramientas de comunicación para un tipo de mensaje muy determinado (los datos) y un tipo de receptor muy determinado (monos con buenos ojos), y como tal, utilizan un código muy especializado.

Los ojos son nuestra principal fuente de información. Se estima que nuestras retinas reciben unos 10 Gbps de información, de los cuales, pasan por el nervio óptico unos 100 Mbps hasta nuestro córtex visual. De hecho, según calculan los neurocientíficos, al menos un tercio de nuestro cerebro está ocupado procesando información visual. Por eso, a veces, cerramos los ojos cuando intentamos concentrarnos: para ser capaces de destinar más recursos a pensar o recordar mejor. En realidad, no es que tengamos una vista muy buena en comparación con otras especies. En lo que realmente somos buenos es en el análisis de la imagen, en extraer información útil a partir de lo que vemos… como caras de otros monos o un león camuflado en las hierbas.

En cambio, nuestra memoria de trabajo es bastante más modesta. Quizás resulte familiar la conocida como ley de Miller: “the magic number seven, plus or minus two¹”. Es uno de los artículos más citados en psicología y, aunque ha sido revisada y matizada posteriormente, viene a decir que, en general, los humanos no podemos retener más de 7 elementos o grupos en nuestra memoria a corto plazo. Es decir, que si nos dan un listado de, pongamos, 10 cosas, nos va a resultar difícil retenerlas todas a la vez en nuestra cabeza y hacer comparaciones entre ellas mentalmente.

Por tanto, la magia de la visualización de datos consiste en convertir “cifras” (números abstractos que requerirían nuestra pobre memoria para ser comparados) en estímulos visuales, de esos que somos tan buenos en analizar.

Por poner un ejemplo, os proponemos encontrar el número más alto en tres tipos de representaciones distintas:

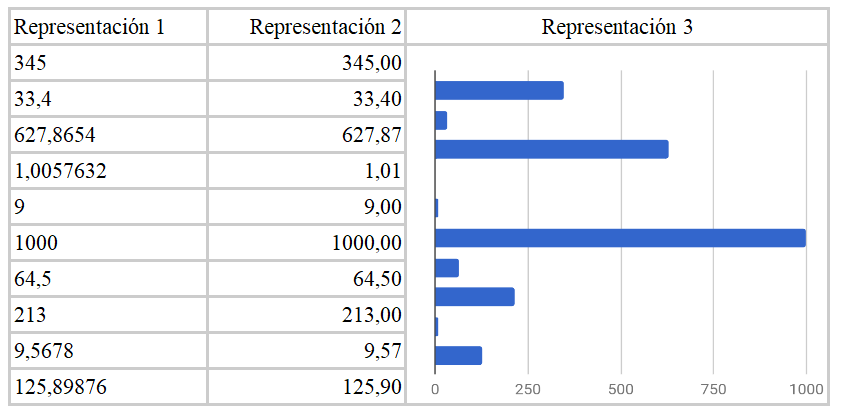
En la primera representación, habréis tenido algunos problemas para encontrarlo, y probablemente hayáis escaneado varias veces la lista, hacia arriba y hacia abajo, para recordar un número o comprobar otra vez dónde estaba la coma de los decimales. En la segunda representación, las cifras están estandarizadas para mostrar dos posiciones decimales. Una vez visto este detalle, la alineación a la derecha hace que encontrar el número más grande sea prácticamente inmediato, dado que “sobresale” hacia la izquierda más que los demás. Pero fijaos que ya hemos recurrido a un truco visual, tomando un atajo que nos permite evitar la memorización, y esto se hace especialmente evidente en la representación final en forma de gráfica.

Existe otro ejemplo muy representativo del poder de nuestros ojos procedente, en este caso, del mundo de los juegos. El juego es como sigue:

1. Hay 2 jugadores.
2. Cada jugador escoge un número del 1 al 9 en su turno.
3. Una vez un número es escogido, nadie puede volver a usarlo.
4. Gana el jugador que primero sume 15 usando 3 números.

Planteado de esta manera, es posible que al lector le cueste hacerse a una idea de en qué consiste el juego o qué estrategia elegir. Parece ciertamente complejo. Jugar requiere retener en la memoria una lista de los números escogidos, las posibles sumas que se forman con ellos y los números eliminados por el otro jugador. Todo un dolor de cabeza. Sin embargo, este mismo juego puede presentarse de manera visual, simplificándose enormemente: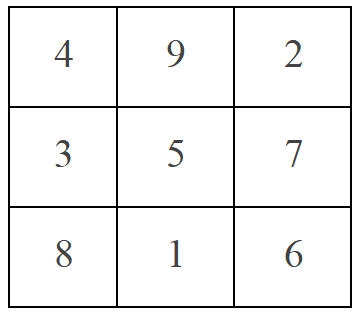
Esta representación visual resume todas las posibles combinaciones, ya que cualquier fila, columna o diagonal suma 15; nos revela, además, algunas propiedades interesantes de estos números. Por ejemplo, el 5 participa en más sumas cuyo resultado es 15 que ningún otro número (ya que se encuentra en el centro de la distribución). Los números pares participan, cada uno, en 3 sumas. Los números impares sólo pueden formar 2 sumas. Son propiedades matemáticas que podríamos haber deducido de haber analizado en detalle el problema inicial. Pero la representación visual nos permite pensar de manera visual, sin abstracciones previas.

En definitiva, la gracia de las gráficas y de las representaciones visuales de cualquier tipo de problema es que convierten datos abstractos, que nuestra memoria de trabajo no puede retener, en estímulos perceptivos, que entran en nuestra cabeza sin necesidad de mediación, sin necesidad de que comprendamos y retengamos cada uno de esos numeritos. Esto las convierte, a su vez, en un arma enormemente peligrosa. Precisamente porque las gráficas hacen innecesario el proceso de lectura (de interpretación mediada y meditada de los datos), es muy fácil engañar y distorsionar los datos recurriendo a su poder.

Referencia: