El propósito de una buena gráfica es mostrar datos de manera precisa y clara. En el popular artículo de 1984 How to Display Data Badly, Howard Wainer toma esta definición como punto de partida para desgranar, no sin cierta sorna, los principales métodos para hacer malas representaciones de datos. Obviamente, las doce reglas de Wainer no deben tomarse al pie de la letra, en el sentido de que cumplir alguna de ellas no necesariamente invalida una gráfica, pero sí representan un compendio de problemas típicos sobre los que es bueno reflexionar a la hora de producir o analizar una visualización de datos. Además, es conveniente incorporar a la reflexión un aspecto no tenido en cuenta por Wainer, como es el soporte de la visualización: no tiene las mismas posibilidades y restricciones una gráfica impresa que una visualización interactiva en la web, o algo que va a salir apenas unos pocos segundos en televisión.

Las dos primeras reglas de Wainer para representar datos mal se derivan precisamente de la primera parte de la definición: mostrar los datos. En sus famosos libros sobre visualización de datos, Edward Tufte concibe dos métricas que hacen referencia a la eficiencia en la representación. Por un lado, define el índice de densidad de datos, que se mediría como “la cantidad de números representados por unidad de área”, y que nos lleva a la primera regla de las malas gráficas: muestra tan pocos datos como sea posible, es decir, minimiza la densidad de datos. Efectivamente, es común lanzarse a hacer gráficos coloristas incluso cuando la cantidad de información a transmitir es realmente pequeña. Pensemos, por ejemplo, en el típico gráfico de tarta con dos porcentajes. En casos como este, hay que preguntarse si realmente aporta algo el gráfico o es suficiente con dar el dato, o hacer una pequeña tabla, cuando el soporte lo permite.

Adicionalmente, una segunda técnica infalible consiste en esconder los datos que se muestran. Esto tiene que ver con lo que Tufte definió como la ratio datos-tinta: minimizar la cantidad de datos representados en relación a la tinta empleadaañade ruido, elementos que no expresan nada y distraen de lo verdaderamente informativo. Esto se hace de diversas maneras, siendo las más habituales las manipulaciones torticeras de la escala, así como la especie de horror vacui que parecen destilar los creadores de algunos engendros.

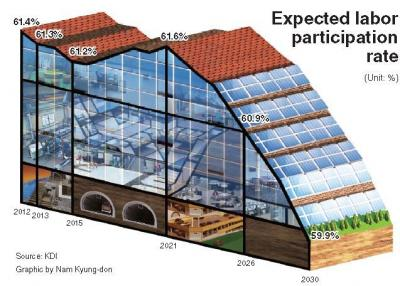
Las siguientes tres reglas de Wainer tienen que ver con la segunda parte de la definición: la precisión en los datos. Ignorar la metáfora visual es probablemente uno de los errores más graves que se pueden cometer. Y aquí, no solo nos referimos a utilizar elementos perceptivamente adecuados, sino a utilizar el elemento visual que mejor se ajusta a la relación que hay en los datos. Por ejemplo, las barras facilitan la comparación entre magnitudes, y una línea evoca una evolución en los valores que une. Por tanto, si utilizamos una línea para unir datos que no tienen una relación de evolución (temporal, por ejemplo), estamos dificultando la lectura en el mejor de los casos, o más probablemente transmitiendo el mensaje equivocado.

La cuarta regla, “solo importa el orden”, hace referencia al truco de usar la longitud como metáfora visual para codificar valores cuando lo que se percibe es el área, pero sirve en general para cualquier versión de pares de elementos gráficos. Quizás la versión moderna más popular de esta regla sea la gráfica de tarta en 3D, donde el elemento visual utilizado es el ángulo, pero lo que se percibe es un volumen completamente distorsionado por la perspectiva.

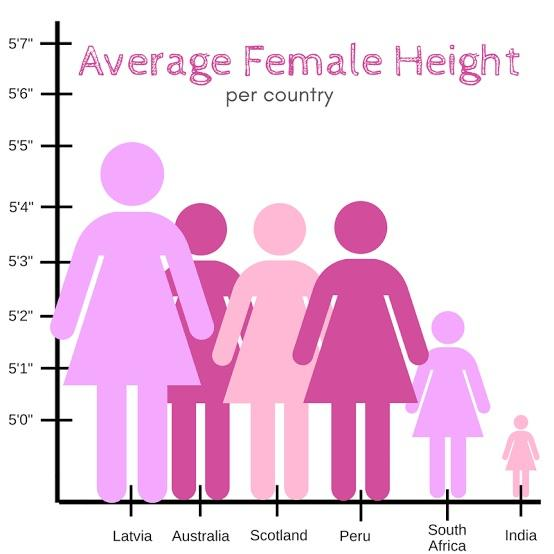
Y llegamos a otra de las reglas a las que más atención hay que prestar para asegurar el fracaso: se trata de mostrar los datos fuera de contexto. Esta es una de las prácticas más habituales entre aquellos que nos aseguran que el paro ha subido o ha bajado en el último mes o en lo que va de año, y de esta manera ocultan el contexto de la serie de datos extendida a varios años, que suele mostrar estacionalidad (mismos patrones que se repiten en los mismos meses del año, como que el paro baja en época de turismo) y tendencias a mayor escala.

Después, se dedican unas cuantas reglas a la idea de la claridad en la representación, aspectos que tienen que ver con detalles más técnicos como cambios de escala a mitad de eje, la enfatización de lo trivial desviando la atención de lo importante, los juegos con el origen (me vienen a la cabeza esas gráficas de barras cortadas, que no empiezan en cero, y por tanto que transmiten una idea de proporción completamente errónea), etiquetado incorrecto, parcial o ambiguo, también enturbiar la gráfica con más elementos de los necesarios, o la regla llamada “¡Austria primero!” (por la costumbre de ordenar países por orden alfabético), que hace referencia a ordenaciones categóricas completamente inútiles por no estar basadas en ningún aspecto de los datos.

Finalmente, Wainer reta al lector: si se ha hecho bien en el pasado, piensa en otra manera de hacerlo. Ciertamente, algunas veces la creatividad da lugar a nuevas visualizaciones que son especialmente buenas para unos datos en particular (véase el ejemplo de Minard que encabeza este artículo), o incluso crean nuevas tendencias y tipos de gráficas. Pero como en todas las disciplinas, si esa creatividad no se sustenta en una dilatada experiencia, habitualmente falla catastróficamente. Y finaliza:

“Por tanto, las reglas para una buena representación son bastante sencillas. Examina los datos de forma suficientemente cuidadosa como para saber qué tienen que decir, y deja que lo digan con el mínimo adorno”.

Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.