Hace unos meses, mientras buscaba información para mis entradas del Cuaderno de Cultura Científica Los números enamorados y ¿Pueden los números enamorarse de su propia imagen?, descubrí dos familias de números primos especiales, los números primos “parientes” (llamados cousin en inglés) y los sexis, ambas relacionadas con los números primos gemelos. Entonces me las guardé en el baúl de los temas pendientes, que acabo de abrir para poder hablar en esta entrada y en la próxima sobre estas familias de números primos.

Pero empecemos por el principio, por los números primos gemelos. Como es bien conocido, los números primos son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos, como el 2, el 3, el 5 o el 7, pero no el 9 (que se puede dividir por 3) o el 12 (que se puede dividir por 2, 3, 4 o 6). Puede leerse más sobre ellos en la entrada Buscando lagunas de números primos, como que existen infinitos números primos, que cada número natural puede expresarse, de forma única, como producto de números primos, qué es la criba de Eratóstenes o sobre el problema de la distribución de los números primos.

Como todos los números pares, a excepción del 2, son números compuestos, no primos, entonces lo más cerca que pueden estar dos números primos, salvo el 2 y el 3 que están pegados, es con solo un número par entre ellos. Y precisamente, a las parejas de números primos que están tan cerca, es decir, con solo un número par entre ellos, o dicho de otra forma, que la diferencia entre ellos es 2, se les llama números primos gemelos, como las parejas 11 y 13, 17 y 19, o 59 y 61. Las parejas de números primos gemelos menores de 500 son (véase la sucesión A0077800 de la enciclopedia online de números enteros):

(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433) y (461, 463).

Por eso en la novela La soledad de los números primos (Salamandra, 2009), del escritor italiano Paolo Giordano, se dice de los protagonistas, Mattia, que es matemático, y Alice: “Mattia pensaba que él y Alice eran eso, dos primos gemelos solos y perdidos, próximos, pero nunca juntos”.

Un primer resultado sobre las parejas de números primos gemelos es que, salvo la pareja (3, 5), son de la forma (6 n – 1, 6 n + 1). Veamos una justificación de este hecho. Un número cualquiera puede escribirse de la forma 6 n + d, para d = 0, 1, 2, 3, 4 o 5. Entonces:

i) si d = 0, 2 o 4, el número 6 n + d no es primo, ya que es divisible por 2;

ii) si d = 3, se puede dividir 6 n + d por 3;

iii) si d = 1, el número es de la forma 6 n + 1;

iv) si d = 5, la forma del número es 6 n + 5 = 6 (n + 1) – 1 = 6 m – 1, si tomamos m = n +1.

De hecho, hemos probado más. Hemos demostrado que todos los números primos, en particular, todos los números no divisibles por 2 y 3, son de una de estas dos formas: 6 n – 1 y 6 n + 1. Por lo tanto, la suma de dos números primos gemelos es divisible por 12 (5 + 7 = 12, 11 + 13 = 24, 17 + 19 = 36, etc).

Más aún, si tenemos una pareja de números primos (6 n – 1, 6 n + 1), entonces el dígito de las unidades del número n debe ser 0, 2, 3, 5, 7 u 8, ya que en otro caso – 1, 4, 6 o 9 – uno de los dos números de esa pareja sería múltiplo de 5.

Lo siguiente que podríamos plantearnos es cuántos números primos gemelos existen. Mientras que la existencia de infinitos números primos es un hecho conocido desde la matemática griega y que posee una sencilla demostración (véase Buscando lagunas de números primos), el problema de si existen infinitas parejas de números primos gemelos sigue estando abierto a día de hoy. Es la conocida como conjetura de los números primos gemelos.

Existen números primos gemelos muy grandes, por ejemplo, la pareja de números primos 1.000.000.000.061 y 1.000.000.000.063, que menciona Keith J. Devlin en su libro El lenguaje de las matemáticas (Ma Non Troppo, 2002), y mucho más grandes aún, como se verá más adelante, pero se desconoce si existen infinitos números primos gemelos. Sin embargo, en los últimos años se ha realizado un importante avance en esta conjetura.

En 2013 nos sorprendió la noticia de que el matemático chino, residente en Estados Unidos, Yitang Zhang, había probado una versión débil de la conjetura de los números primos (el correspondiente artículo fue publicado en 2014 en la prestigiosa revista de investigación matemática, Annals of Mathematics). En concreto, había demostrado que existen infinitas parejas de números primos cuya diferencia entre ellos es menor que 70 millones (70.000.000). No era la conjetura de los números primos gemelos, pero era un gran paso, ya que se había fijado una cota finita que, aunque no era 2 (que establece la conjetura para los números primos gemelos), al menos era finita, para la existencia de infinitas parejas de números primos cuya diferencia entre ellos fuera menor que esa cota.

A partir del resultado de Yitang Zhang, el matemático australiano-americano Terence Tao, propuso un proyecto polymath (que son proyectos colaborativos masivos para resolver problemas matemáticos) para reducir la cota de Zhang. Esta ha conseguido reducirse hasta 246. Es decir, existen infinitas parejas de números primos, cuya diferencia entre ellos es menor que 246. Dentro de ese conjunto infinito de parejas de números primos está el conjunto de los números primos gemelos (cuya diferencia es 2), el conjunto de las parejas de números primos cuya diferencia es 4, que son los llamados primos parientes, o el de aquellas cuya diferencia es 6, los primos sexis, que aún no sabemos si ellos solos son conjuntos infinitos o no, pero también todas las demás parejas de números primos con una diferencia menor que 246, como 29 y 41 (cuya diferencia es 12) o 47 y 269 (cuya diferencia es 222).

Más aún, asumiendo la conjetura de Elliot-Halberstam, sobre la distribución de números primos en progresión aritmética, y una generalización de la misma, se ha demostrado que la cota puede reducirse a 12 y 6.

Como puede verse en la página web dedicada a los números primos y sus records, The Prime pages, los números primos gemelos más grandes conocidos, a día de hoy, fueron obtenidos en septiembre de 2016, y son los números

2.996.863.034.895 · 2^1.290.000 – 1 y 2.996.863.034.895 · 2^1.290.000 + 1,

que tienen nada más y nada menos que 388.342 dígitos.

Otra cuestión interesante que nos podríamos plantear, es cuál es el porcentaje de parejas de números primos gemelos dentro del conjunto de todos los números primos, entendiendo que estamos contando solo el primer primo de la pareja, es decir, el primo p tal que p + 2 es también primo. Si miramos los listados existentes de ambos conjuntos, veremos que, entre los 100 primeros números, hay 25 números primos (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97) y 8 números primos p tales que p + 2 es también primo (3, 5, 11, 17, 29, 41, 59, 71), es decir, parejas de números primos gemelos, luego hay un 32% de parejas de números primos gemelos. Si tomamos ahora los 1000 primeros números, hay 168 números primos y 35 parejas de números primos gemelos, luego un 20,8%. Y va disminuyendo el porcentaje, de manera que cuando tomamos los primeros un millardo de números (1.000.000.000), hay 50.847.534 números primos, pero solo un 6,7% son primos p tales que p + 2 es primo, 3.424.506.

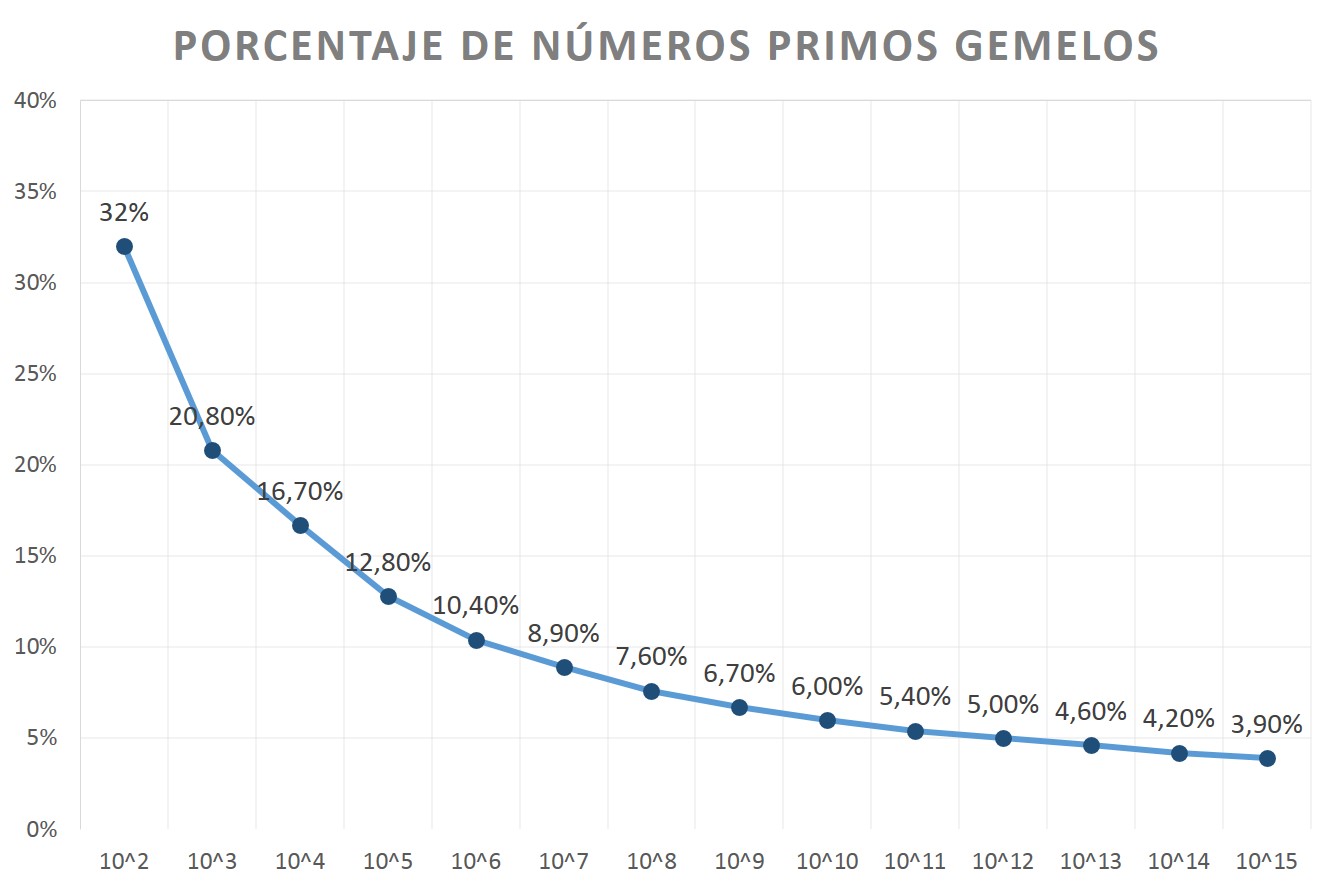
Como puede observarse, cada vez hay menos números primos gemelos (en realidad, primos p tales que p + 2 es primo), dentro del conjunto de números primos.

Un resultado curioso relacionado con los números primos gemelos es el conocido como teorema de Brun, demostrado por el matemático noruego M. Viggo Brun (1885-1978) en 1919.

Teorema de Brun (1919): La suma de los recíprocos de los números primos gemelos

es convergente, y converge al número B₂, la conocida como constante de Brun, que tiene un valor aproximado de 1,902160583104 (esta aproximación fue obtenida en 2002, por Pascal Sebah y Xavier Gourdon).

Si la anterior serie, la suma de los recíprocos de los números primos gemelos, fuese divergente, es decir, que la secuencia infinita de sumas parciales de la serie no tuviese límite, entonces podríamos afirmar que existen infinitos números primos gemelos. Esto se debe a que si fuesen finitos la serie sería convergente, ya que la suma tendría un número finito de sumandos, luego sería finita, tendría límite. Sin embargo, la serie es convergente, por lo que no podemos deducir de ahí que sea una familia finita o infinita.

Por otra parte, si la constante de Brun B₂ fuese un número irracional, es decir, que no se puede escribir como cociente de dos números enteros, podríamos afirmar que entonces existen infinitos números primos gemelos. Esto se debe a que, si fuesen finitos, la serie anterior sería una suma finita de números racionales, luego racional. Pero se desconoce si B₂ es racional o irracional.

Continuando con nuestro interés por los números primos gemelos, podríamos plantearnos si existen ternas de números primos gemelos. La respuesta es negativa, salvo para la terna (3, 5, 7), ya que cada tres números impares consecutivos, uno de ellos necesariamente es múltiplo de 3. Es fácil observar esto. Todo número puede escribirse como 3 n + r, con r = 0, 1 o 2, entonces tres números impares consecutivos pueden escribirse de la forma 3 n + r, 3 n + r + 2 y 3 n + r + 4 = 3 (n + 1) + r + 1. Si r = 0, el primer número es múltiplo de 3, si r = 1, lo es el segundo, y si r = 2, el múltiplo de 3 es el tercero.

En conclusión, no hay ternas de números primos gemelos. Lo más cerca que pueden estar tres números primos entre sí es cuando son de la forma (p, p + 2, p + 6), como (5, 7, 11) o (11, 13, 17), y de la forma (p, p + 4, p + 6), como (7, 11, 13) o (13, 17, 19), a los cuales se les llama números primos trillizos.

Los números primos trillizos de la forma (p, p + 2, p + 6), menores de 500, son (véase la sucesión A022004 de la enciclopedia online de números enteros):

(5, 7, 11), (11, 13, 17), (17, 19, 23), (41, 43, 47), (101, 103, 107), (107, 109, 113), (191, 193, 197), (227, 229, 233), (311, 313, 317), (347, 349, 353), (461, 463, 467).

Mientras que los números primos trillizos de la forma (p, p + 4, p + 6), menores de 500, son (véase la sucesión A022005):

(7, 11, 13), (13, 17, 19), (37, 41, 43), (67, 71, 73), (97, 101, 103), (103, 107, 109), (193, 197, 199), (223, 227, 229), (277, 281, 283), (307, 311, 313), (457, 461, 463).

Además, la terna de números trillizos, de la forma (p, p + 2, p + 6), más grande que se conoce en la actualidad, obtenida en abril de 2019 (véase The Prime pages), es

4.111.286.921.397 x 2^66.420 – 1,

4.111.286.921.397 x 2^66.420 + 1,

4.111.286.921.397 x 2^66.420 + 5,

que tienen 20.008 dígitos. Mientras que para la forma (p, p + 4, p + 6), los números primos trillizos más grandes, obtenidos en abril de 2013 (véase The Prime pages), son

6.521.953.289.619 x 2^55.555 – 5

6.521.953.289.619 x 2^55.555 – 1

6.521.953.289.619 x 2^55.555 + 1,

con 16.717 dígitos cada uno. Además, de forma similar a la conjetura de los números primos gemelos, existe una conjetura sobre la existencia de infinitos números primos trillizos.

En general, nos podemos plantear el estudio de las familias de los grupos de k números primos más próximos posibles, que podemos llamar, para k = 4, cuatrillizos, para k = 5, quintillizos, luego sextillizos, septillizos, octillizos, nonillizos, etcétera y, en general, para cualquier k, números primos k-tillizos.

Los números primos cuatrillizos son de la forma (p, p + 2, p + 6, p + 8). Las primeras cuaternas de números primos cuatrillizos (véase la sucesión A007530) son

(5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089).

Además, puede demostrarse que los números primos cuatrillizos son de la forma

(30 n + 11, 30 n + 13, 30 n + 17, 30 n + 19),

salvo la cuaterna inicial (5, 7, 11, 13). Este resultado, y otros similares, ayudan a la hora de encontrar números primos cuatrillizos (véase, por ejemplo, el artículo Two Algorithms to Find Primes in Patterns, de Jonathan Sorenson).

Si tenemos una cuaterna de números primos cuatrillizos (p, p + 2, p + 6, p + 8) tal que uno de los números, p – 4 o p + 12, es primo, entonces se tiene una quinterna de números primos lo más próximos posibles entre ellos, es decir, una quinterna de números primos quintillizos. Por lo tanto, los números primos quintillizos son de la forma (p, p + 2, p + 6, p + 8, p + 12), como las quinternas (5, 7, 11, 13, 17) y (11, 13, 17, 19, 23), o de la forma (p, p + 4, p + 6, p + 10, p + 12), como (7, 11, 13, 17, 19) y (97, 101, 103, 107, 109).

Mientras que los números primos sextillizos son de la forma (p, p + 4, p + 6, p + 10, p + 12, p + 16), como (7, 11, 13, 17, 19, 23) y (97, 101, 103, 107, 109, 113), y así podríamos seguir con más agrupaciones próximas de números primos.

Despidamos la primera parte de esta miniserie de entradas sobre los números primos gemelos, parientes y sexis, y otras familias relacionadas, con otra obra relacionada con los números primos de la artista donostiarra Esther Ferrer.

Bibliografía

1.- Wolfram Mathworld: Twin Primes

2.- Wikipedia: Twin prime

3.- Yitang Zhang, Bounded gaps between primes, Annals of Mathematics 179 (3), pp. 1121–1174, 2014.

4.- The Prime pages

5.- Chris, Di and Matthew Stevenson, Hugin Home Page: Prime numbers

6.- X. Gourdon, P. Sebah: Introduction to Twin Primes and Brun’s Constant Computation

7.- Wolfram Mathworld: Prime Triplet

8.- Wikipedia: Prime triplet

9.- Wikipedia: Prime quadruplet

10.- Jonathan Sorenson, Two Algorithms to Find Primes in Patterns

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica