El gato de Arnold
Las matemáticas son parte de la física. La física es una ciencia experimental, una de las ciencias naturales. Las matemáticas son la parte de la física en la que los experimentos son baratos.
Vladimir I. Arnold, en [1].

Con esta contundente afirmación sobre la educación matemática comenzaba su artículo el prolífico matemático ruso Vladímir Ígorevich Arnold (1937-2010). El científico era muy crítico con la manera de enseñar matemáticas debido al nivel de abstracción que estaban alcanzando en aquella época. El grupo Bourbaki impulsó en Francia esta alta conceptualización de las matemáticas que fue posteriormente adoptada en otros países. Arnold opinaba que esta elección tenía un impacto negativo en la educación matemática, que había otra manera más natural y satisfactoria de introducir conceptos y problemas. Lamentaba que, en este intento por construir una “matemática pura” siguiendo el método axiomático-deductivo, se había llegado a rechazar el esquema clásico en física («experiencia – modelo – estudio del modelo – conclusiones – verificación por la experiencia») para reemplazarlo por el esquema «definición – teorema – demostración».
En [1], Arnold comentaba con sorna:
A la pregunta «¿Cuánto son 2+3?» un alumno de escuela francés ha contestado «3+2 porque la suma es conmutativa.». ¡Ni siquiera sabía a qué era igual esta suma, ni siquiera entendía lo que le estaban preguntando!
¿Exageraba Arnold o tenía razón en sus contundentes afirmaciones? Supongo que habrá opiniones variadas. Así que dejamos aparte las opiniones de Arnold para centrarnos en su gato…
En la teoría de sistemas dinámicos, la «aplicación gato de Arnold» es un ejemplo de difeomorfismo de Anosov sobre el toro. Para aquellas personas que deseen conocer la definición y propiedades de esta aplicación, dejamos algunas referencias al final de esta anotación. Dicho de manera sencilla, la «aplicación gato de Arnold» es una transformación del toro en sí mismo inducida por una aplicación lineal sobre el plano.
Recordemos, antes de seguir, que el toro puede obtenerse como el cociente de un cuadrado con las identificaciones mostradas en la figura:
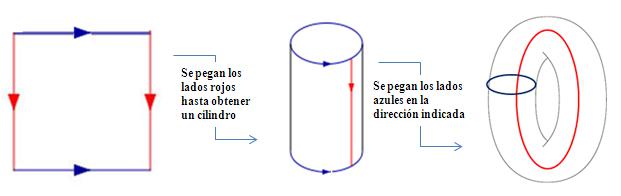
Siguiendo su máxima de experimentar, Arnold mostró los efectos de esta aplicación usando la imagen de un gato dibujada sobre un toro, de allí el nombre de esta aplicación. ¿Y cómo lo hizo? Colocó la imagen de un gato sobre un cuadrado –teniendo en cuenta las identificaciones indicadas anteriormente, la imagen puede pensarse sobre un toro– la deformó siguiendo la definición de la «aplicación gato de Arnold» y recortó la imagen resultante en trozos para recomponerla de manera adecuada sobre el cuadrado –y por lo tanto sobre el toro, tras cocientar–.

Este proceso se puede repetir. Es decir, a la imagen obtenida se le puede volver a aplicar la «aplicación gato de Arnold» y observar cómo evoluciona este sistema.
Existe un análogo discreto de la «aplicación gato de Arnold». Al tratarse de una transformación biyectiva de una imageni, sabemos que existe un menor número entero, k, de manera que realizando k veces la transformación se vuelve a obtener la imagen original.
La imagen de debajo –de 150 por 150 píxeles– representa a un gato –no pertenece a Arnold; es del autor de la imagen, Claudio Rocchini–. Podemos observar el efecto de la transformación tras 1, 3, 132, 155, 157, 200, 211, 240, 275, 299 y 300 iteraciones, momento en el que la imagen original reaparece. Es decir, el número entero k aludido antes es de 300 para una imagen de 150 por 150 píxeles.

A continuación puede verse una simulación de cómo evoluciona la «aplicación gato de Arnold» discreta sobre una imagen de 74 por 74 píxeles. En este caso el número entero k es 114, es decir, se recupera la imagen original tras 114 iteraciones. Observar, además que en la iteración 57 aparece la imagen original, pero girada 180 grados.

Sin duda sorprende recuperar la imagen de partida tras este aparente comportamiento caótico. Estas sorpresas forman parte de la belleza de las matemáticas.
Por cierto, si te apetece experimentar con tus propias imágenes, en las referencias [4] y [5] puedes hacerlo online.
Referencias
[1] Vladimir I. Arnold, «Sur l’éducation mathématique», Gazette de Mathématiciens 78 (1998), 19-29 (traducido del ruso por J.- M. Kantor)
[2] Arnold’s cat map, Wikipedia (consultado el 18 de enero de 2020)
[3] David D. Nolte, Vladimir Arnold’s Cat Map, Galileo Unbound, 16 junio 2019
[5] Jason Davies, Arnold’s Cat Map, 2012
Nota:
i Una transformación biyectiva de una imagen de n por m píxeles es una modificación de esta imagen sobre sí misma: cada pixel se desplaza de su lugar a otro –y el que ocupa ese lugar se mueve a otro sitio–. Ningún pixel desaparece, sólo cambia de posición. En matemáticas se habla de una permutación de los estos píxeles. El conjunto P de las permutaciones sobre un conjunto finito forma un grupo –el grupo simétrico, que en este caso, además, es un grupo finito–. Puede demostrarse que si P es una permutación de este tipo, existe un número entero k tal que si P se aplica k veces se recupera la transformación identidad –la permutación que no cambia nada–.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

juan simon
Interesante artículo. La teoría de conjuntos no hizo nada bueno en la Egb en España -El carácter lúdico de las matemáticas: Un buen juego matemático vale por muchos teoremas»> J. E. Littlewood.