Hace unas semanas, un tipo saxofonista alemán llamado Armin Küpper subió un curioso canon a su canal de Youtube¹. La primera voz la interpretaba él mismo, con su instrumento. La segunda voz se la devolvía una enorme tubería. No en vano, “Pipeline funk” es el título de su composición.

Y ahora, la pregunta: viendo el vídeo, ¿sabrías decir cuánto mide, aproximadamente, la tubería? Es un acertijo molón porque el cálculo que requiere es bastante sencillo. El saxofonista toca en un extremo del tubo, que se comporta como una guía de onda (una especie de fibra óptica pero con ondas acústicas en lugar de electromagnéticas). El sonido lo recorre por completo y rebota en el extremo opuesto. Conocemos, además, la velocidad del sonido, unos 343 m/s si suponemos que en Alemania en estas fechas no hace demasiado frío. Ahora basta medir el tiempo que separa la primera voz de su doble, multiplicar ambos valores y dividir el resultado entre dos (teniendo en cuenta que el sonido hace un camino de ida y vuelta).

Y listo, ¿lo tienes?

Si las matemáticas de la ESO no te fallan, habrás obtenido algún resultado entre 170 y 200 metros. Y si piensas como casi la mayoría de los curiosos a quienes les planteé este mismo acertijo hace un par de semanas en Twitter, lo único farragoso del problema habrá sido tener que medir la duración del lapso entre la melodía y su eco. A orejímetro, quizás hayas estimado 1 segundo, aproximadamente y de aquí procede la mayor fuente de error. Otros lectores, con más paciencia, usaron incluso programas de edición de audio y tablas de Excel para alcanzar mayor precisión. Mi casa, en cambio, está llena de músicos, así que ese punto del problema resultaba relativamente sencillo:

— Suena bastante más lento que el concierto de Mozart… así que le echo unos 100 pulsos por minuto. Pongamos que 1,2 segundos cada compás.

El concierto de Mozart del que habla mi pareja es este. Los pulsos por minuto (ppm) son una medida de la velocidad a la que se suceden sus compases. Iñaki, además de investigador, es clarinetista y siempre recurre a su propia memoria musical y muscular, ligada a una obra que ha interpretado cientos de veces, para estimar duraciones temporales. Tampoco es que sea el primer científico de la historia en usar un truco así.

Hacia 1604, Galileo Galilei estaba estudiando el movimiento de los cuerpos acelerados por la gravedad. En aquella época, por desgracia, no existían cronómetros demasiado precisos, ni nada que se pareciera a un sistema de unidades estándar. Para llevar a cabo sus experimentos, a menudo Galileo inventaba sus propias medidas y sistemas de calibración. En, en este caso, el físico italiano necesitaba algún recurso que le permitiese medir lapsos de tiempo de igual duración. Como los pulsos de una canción. Y no le valía cualquier canción. Necesitaba un ritmo contundente, bien definido, algo que se pudiera bailar, vaya, parecido al ritmo de un buen tema pop.

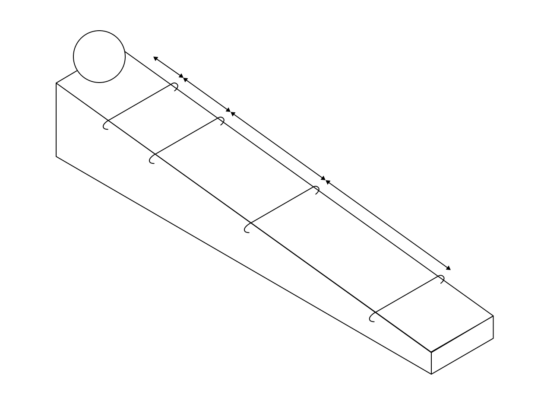
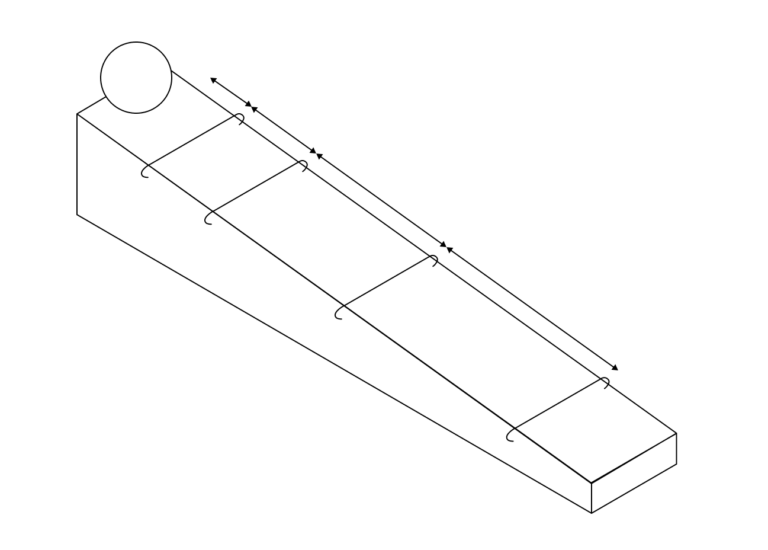
Después, colocó una serie de trastes sobre un plano inclinado. Su objetivo era analizar el movimiento de una pelota rodando por su pendiente. Al pasar sobre los trastes la pelota emitía un pequeño ruido, así que Galileo solo tenía que moverlos hasta sincronizarlos con los pulsos de su canción. El resultado eran una serie de distancias desiguales sobre la rampa, proporcionales, en su eje vertical, al tiempo transcurrido desde el inicio de la canción (la corchea enésima) al cuadrado.

Galileo descubrió la matemática de los cuerpos acelerados mientras cantaba una canción popular. En mi cabeza, era algo parecido a Shakira aunque probablemente los musicólogos no están muy de acuerdo conmigo en esto. Lo sorprendente es que, a pesar de lo rudimentario de su método, ¡sus medidas alcanzaron una precisión de 1/64 de segundo²! La ventaja de utilizar una canción para medir el tiempo es que su patrón repetitivo permite tomar muchas medidas, sucesivas, en lugar de una sola aislada. En el caso del canon de la tubería, por ejemplo, al sincronizar la canción con un metrónomo, es posible ajustar no sólo “una” medida del tiempo, sino todas las que abarque la canción, pudiendo así reducir el error.

Por otra parte, los humanos somos especialmente hábiles recordando los tempos de las canciones de manera precisa, especialmente dentro de cierto rango. En un experimento de 1996³, Daniel J.Levitin y Perry R. Cook mostraron que la mayoría de los oyentes recordaban y cantaban diversas canciones pop a la misma velocidad que la grabación original con un margen inferior al 8 %. Esta habilidad resulta fundamental en campañas como la de la British Heart Foundation, que tenía por objetivo enseñar técnicas de primeros auxilios a la población ayudándose del ritmo de una canción. Si alguna vez necesitas socorrer a alguien con un paro cardiaco, recuerda esto: lo primero, llama al 112. Solo después, insiste con “Staying alive” (tempo: 104 ppm).

¿Y el canon de la tubería?, ¿cómo de larga era?, ¿cuánto duraban sus repeticiones? Bien, Iñaki había estimado a oreja que el canon sonaba a unos 100 ppm. Esto permite calcular rápidamente la duración de los pulsos: 60/100=0,6 segundos lo que nos da un compás (el lapso que separa a la melodía de su eco) de 1,2 segundos. Echando mano a un editor de audio resulta que los lapsos duraban un poquillo menos: 1,17 segundos. En total, un error de menos del 3%, que no está nada mal para no haber sacado ni siquiera el reloj. Podemos concluir que la tubería mide unos 200 metros.

Notas y referencias: