Les structures élémentaires de la parenté –Las estructuras elementales del parentesco– es el título de la tesis defendida por el antropólogo Claude Lévi-Strauss en 1948 –revisada y publicada en 1949– en la que sostenía la teoría de la alianza.

El antropólogo recurrió a un amigo, el matemático André Weil, para axiomatizar los sistemas de parentescos que describía en su tesis. De hecho, Weil escribió un apéndice –Sur l’étude algébrique de certains types de lois du mariage (Sobre el estudio algebraico de algunos tipos de leyes matrimoniales)– que Lévi-Strauss incorporó a la primera parte de su tesis.

En sus notas autobiográficasⁱ, André Weil dedicaba varios párrafos a este episodio con Lévi-Straussⁱⁱ:

A New York, [Lévi-Strauss] s’était lancé dans un vaste travail de sociologie théorique qui devint sa thèse de doctorat (aujourd’hui célèbre) sur les structures élémentaires de la parenté. Un jour, dans l’étude d’un certain type de mariage, il se heurta à des difficultés inattendues et pensa qu’un mathématicien pourrait lui venir en aide.

D’après ce qu’ont observé les sociologues travaillant « sur le terrain », les lois de mariage des tribus indigènes d’Australie comportent un mélange de règles exogamiques et endogamiques dont la description et l’étude posent des problèmes combinatoires parfois compliqués. Le plus souvent le sociologue s’en tire par l’énumération de tous les cas possibles dans l’intérieur d’un système donné. Mais la tribu des Murngin, à la pointe Nord de l’Australie, s’était donné un système d’une telle ingéniosité que Lévi-Strauss n’arrivait plus à en dérouler les conséquences. En désespoir de cause il me soumit son problème.

Le plus difficile pour le mathématicien, lorsqu’il s’agit de mathématique appliquée, est souvent de comprendre de quoi il s’agit et de traduire dans son propre langage les données de la question. Non sans mal, je finis par voir que tout se ramenait à étudier deux permutations et le groupe qu’elles engendrent. Alors apparut une circonstance imprévue. Les lois de mariage de la tribu Murngin, et de beaucoup d’autres, comportent le principe suivant : « Tout homme peut épouser la fille du frère de sa mère, » ou, bien entendu, l’équivalent de celle-ci dans la classification matrimoniale de la tribu. Miraculeusement, ce principe revient à dire que les deux permutations dont il s’agit sont échangeables, donc que le groupe qu’elles engendrent est abélien. Un système qui à première vue menaçait d’être d’une complication inextricable devient ainsi assez facile à décrire dès lors qu’on introduit une notation convenable. Je n’ose dire que ce principe a été adopté pour faire plaisir aux mathématiciens, mais j’avoue qu’il m’en est resté une certaine tendresse pour les Murngin.

La tribu de los Murngin estudiada por Lévi-Strauss vivía en el noreste de la Tierra de Arnhem (Australia); su estructura de parentesco es bastante compleja. Más sencilla es la de la tribu de los Kariera que vivían en el noroeste. Según la descripción de Lévi-Strauss, los Kariera se dividen en cuatro clanes: Banaka, Karimera, Burung, Palyeri. Esta división rige, entre otros, los matrimonios –siempre con personas del sexo opuesto– y las filiaciones. Una persona Banaka se casa con una Burung y una Karimera con una Palyeri. Respecto a la descendencia, las hijas o hijos de un hombre Banaka y una mujer Burung son Palyeri, mientras que los hijos de un hombre Burung y una mujer Banaka son Karimera. Del mismo modo, los descendientes de un hombre Karimera y una mujer Palyeri son Burung, y los de una mujer Karimera y un hombre Palyeri son Banaka. Esto puede resumirse en la siguiente tabla:

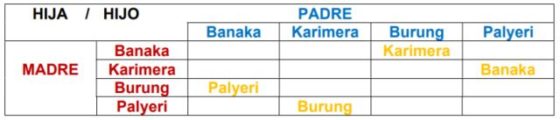
André Weil estudió la situación propuesta por Lévi-Strauss, generalizándola a una tribu con n clanes, lo que le permitía tratar diferentes casos. Vamos a detallar en el caso n=4 el estudio de Weil con la situación propuesta por Lévi-Strauss. Sea K el conjunto de los clanes de la tribu Kaiera:

K= {Banaka, Karimera, Burung, Palyeri}.

Definimos tres permutaciones de K en K –f, p y m– que expresan las relaciones matrimoniales (f), las filiaciones patrilineales (p, tanto de padres a hijas/os como de hijas/os a padres) y las filiaciones matrilineales (m, tanto de madres a hijas/os como de hijas/os a madres) antes indicadas.

La tabla 1 puede entonces reescribirse en términos de funciones:

Observamos que una persona x tiene dos tipos de primos cruzados: los hijos e hijas de las hermanas de su padre y los hijos e hijas de los hermanos de su madre. El padre –y las hermanas del padre– de x son miembros del clan p(x); por lo tanto, los hijos e hijas de sus tías por parte de padre pertenecen al clan m(p(x)). La madre –y los hermanos (varones) de la madre– de x son miembros del clan m(x); por lo tanto, los hijos e hijas de sus tíos (varones) por parte de madre pertenecen al clan p(m(x)). En la tabla 3 se resumen estas propiedades (donde m◦p denota la composición de las funciones p y m):

Como m(p(x)) = p(m(x)) = f(x), se deduce que x puede casarse con m(p(x)) y p(m(x)). Es decir, una persona puede casarse con cualquiera de sus primos cruzados del sexo opuesto.

Observamos también que p◦p = m◦m = id, donde id es la función identidad (ver tabla 1). Una persona del clan x tiene entonces dos clases de primos paralelos: los hijos e hijas de las hermanas de su madre –ya que m◦m = id– y los hijos e hijas de los hermanos de su padre –por ser p◦p = id–. Como todos los primos paralelos de una persona pertenecen al mismo clan, se deduce que no pueden casarse entre ellos.

Si P={id,f,p,m} y se dota a este conjunto de la operación de composición de funciones, las anteriores relaciones dicen que el par (P,◦) es un subgrupo abeliano del grupo de las permutaciones de K. De hecho es (isomorfo a) el grupo de Klein, el menor grupo no trivial y no cíclico.

Este es un caso particular de estudio matemático de las estructuras de parentesco abordadas por Weil. Sin embargo, este modelo posee algunas dificultades pues permitiría teóricamente el matrimonio entre parientes directos de dos generaciones diferentesⁱⁱⁱ. Así que ha sido retrabajado por otros muchos matemáticos, como puede verse en las referencias propuestas.

Referencias

• Klaus Hamberger, Espaces de la parenté, L’Homme 195-196 (2010) 451-468

• Paul Jorion et Gisèle De Meur. La Question murngin, un artefact de la littérature anthropologique. L’Homme 20 (2) (1980) 39-70

• Paul Lavoie, Claude Lévi-Strauss et les mathématiques, Bulletin AMQ 52 (2) (2012) 37-61

Notas: