El modelo SIR, un enfoque matemático de la propagación de infecciones
Javier Duoandikoetxea
En este periodo atípico que vivimos a menudo se subraya el valor y el papel que juega la ciencia. En este contexto, también las matemáticas hacen su aportación. Entre otras cosas, ponen a nuestra disposición herramientas que nos permiten prever la evolución de las epidemias. Pronto cumplirán su primer centenario los primeros modelos matemáticos propuestos para tal fin.
Los modelos matemáticos
Los modelos matemáticos se sirven de herramientas matemáticas para estudiar un fenómeno de la vida real de manera abstracta y simplificada. Para ello se expresan mediante una formulación matemática las relaciones entre las magnitudes que intervienen en el fenómeno. El uso y el éxito de los modelos matemáticos varía de unas ciencias a otras. Es obvio que la física está muy matematizada, pero en las ciencias de la vida, por ejemplo, la presencia de las matemáticas no ha sido tan notoria. Hay quien piensa que todo lo relacionado con la vida es demasiado complejo para ajustarse a los modelos simples y abstractos de las matemáticas. Parece que uno de los retos de la matemática aplicada en el siglo XXI será precisamente la ampliación del uso de la matemática en las ciencias de la vida.
En cualquier caso, las primeras propuestas para la aplicación de modelos matemáticos en biología vienen de lejos, si bien en los últimos tiempos es cuando se han producido importantes avances en este terreno. Así, los modelos aplicados a las enfermedades infecciosas no son nuevos, como atestigua el que trataremos aquí, presentado en un artículo que William Ogilvy Kermack y Anderson Gray McKendrick publicaron en 1927 —esto es, hace casi cien años— con el título A Contribution to the Mathematical Theory of Epidemics.

El modelo SIR
Los miembros de una población se clasifican en tres grupos: susceptibles (S=susceptible), infectados (I=infected) y recuperados (R=recovered). Cada miembro de la población pertenece únicamente a uno de los tres grupos en un momento dado. Sin embargo, se puede pasar de un grupo a otro, aunque solo en una dirección, como se muestra en el siguiente esquema:

Por tanto, un miembro susceptible se puede contagiar (pasar de S a I) y uno contagiado se puede recuperar (pasar de I a R) o puede morir. En este modelo se supone que la recuperación proporciona inmunidad y no se regresa al grupo S.
Las personas que fallecen por la enfermedad se incluyen también en el grupo R, con lo que la población total se mantiene constante. Como se habrá notado, el modelo introduce una simplificación, pues no tiene en cuenta ni los nacimientos ni las muertes por otros motivos. Existen modelos más complejos que también contemplan esos casos.
Ecuaciones
Sea t la variable que indica el tiempo y S(t), I(t) y R(t) el número de personas que hay en cada grupo en un momento t determinado. Por las razones expuestas, su suma es una constante. Sea N el tamaño de la población, es decir, S(t) + I(t) + R(t) = N, para todo t. Para plantear las ecuaciones, es necesario formular la velocidad de cambio de esas tres funciones. La expresión matemática de la velocidad es una derivada.
He aquí las ecuaciones del modelo SIR:
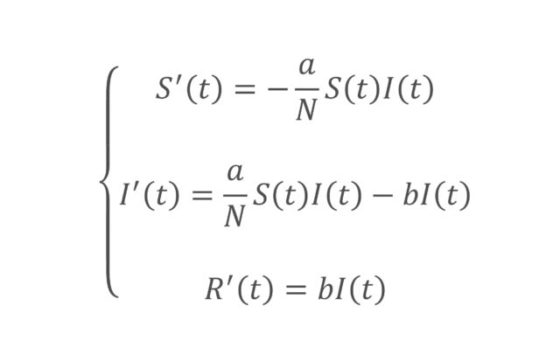
El contacto entre personas susceptibles e infectadas causará el contagio de algunos miembros de S. Dado que el riesgo de contagio depende de los contactos entre miembros de los grupos S e I, la hipótesis del modelo SIR es que sus encuentros son proporcionales al producto de S por I. Además existe un factor llamado tasa de transmisión que debe multiplicarse por dicho producto para calcular la velocidad de cambio del grupo susceptible. Expresamos esa tasa como a/N. El término figura en la ecuación porque expresa la velocidad con que se pasa de S a I. Dado que en el proceso el n.º de susceptibles disminuye y el de personas infectadas aumenta, es negativo para S’ y positivo, en cambio, para I’.
Por otra parte, quienes se curen o fallezcan pasarán de I a R. Para calcular cuántas personas lo hacen tenemos la tasa de recuperación, que ha de multiplicarse por el número de personas infectadas. Por eso aparece el término en las ecuaciones; es negativo para I’, porque reduce el n.º de personas infectadas y positivo para R’, porque hacer aumentar el n.º de recuperadas.
Para resolver las ecuaciones es necesario disponer de los datos iniciales, es decir, el n.º de miembros de cada grupo en el momento en que t=0. Se puede suponer que al principio I(0) = 1 (paciente cero), pero cabe la posibilidad de que fuera superior a uno. Además, tendremos que S(0) > 0 , pues para que haya contagio es necesario que haya susceptibles.
Soluciones de la ecuación
No se puede calcular la solución exacta de las ecuaciones, pero esto no es un problema, pues se pueden obtener soluciones aproximadas por ordenador. En cualquier caso, aun sin resolver el sistema de ecuaciones, las herramientas matemáticas nos permiten determinar algunas propiedades cualitativas de las soluciones.
Así, se observa que el comportamiento de las soluciones depende del número a/b. Se trata del número R0, la tasa básica de reproducción, en este caso. Si R0 > 1, la infección comenzará a extenderse, y si R0 < 1, esto no ocurrirá. De todas formas, si bien ese valor básico tiene incidencia al principio, posteriormente es mejor usar la tasa de reproducción efectiva o aS(t)/Nb. Como al principio S(0) y N son prácticamente iguales, cuando t=0 es casi igual a R0, pero después va reduciéndose a la vez que S.
Plantear ecuaciones formales es fácil, lo problemático es asignar unos valores adecuados a los parámetros a y b. El segundo se puede decidir observando el tiempo que se tarda en recuperarse de la enfermedad. Sin embargo, es más difícil asignar un valor a a. Si partimos de cero, ese valor es desconocido, por lo que es necesario observar el ritmo de contagios del principio. A veces se emplean datos de otros territorios o periodos, pero estos pueden proporcionar información errónea. Además, este modelo simplificado mantiene a y b constantes a lo largo del tiempo, pero en la práctica se pueden adoptar medidas para cambiar estos valores.
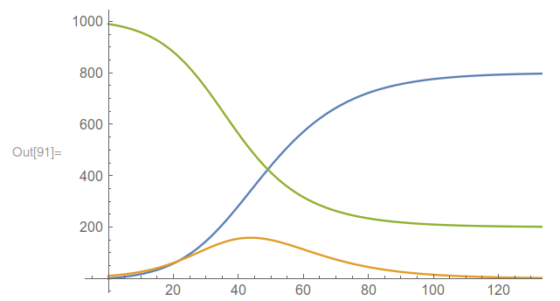
Sea como fuere, una de las conclusiones de las ecuaciones es que el valor I(t) tiende a 0 según avanza el tiempo, es decir, se reduce el n.º de personas infectadas. De hecho, el análisis de las ecuaciones indica que debe darse un valor umbral para que la infección se propague. Si el n.º de susceptibles es inferior a ese valor, la infección no se propaga, es decir, dejará de haber personas infectadas, aunque siga habiendo susceptibles. Viendo los datos reales no se percibe la existencia de este umbral, por lo que el modelo matemático fue esencial para llegar a esa conclusión.
Por otro lado, la función I(t) llega a un valor máximo y luego comienza a descender, sin incrementarse de nuevo. Es decir, tiene un único pico. Esta es otra de las propiedades que revela el modelo matemático. No obstante, hay que recordar que el modelo es muy simple y a veces la realidad puede ser distinta.
Intervención pública
El modelo muestra que se puede frenar la propagación de la infección incidiendo en la tasa de reproducción efectiva. En el caso de los virus, se pueden emprender las siguientes acciones:
- Acortar el tiempo de la enfermedad con medicamentos.
- Reducir los contactos entre personas susceptibles e infectadas mediante medidas de aislamiento.
- Reducir la probabilidad de transmisión mediante el lavado frecuente de manos y el uso de mascarillas.
- Reducir el valor inicial S(0) mediante vacunas.
Nos suenan, ¿verdad? Las lectoras y lectores pueden pensar que estos consejos se formularon en el contexto de la Covid-19. Pues no, los he copiado de un artículo de divulgación de 2013 y se referían a la gripe. Tiene presente la evolución de las soluciones de las ecuaciones matemáticas, ya que reducir a y S(t) y aumentar b son formas de minorar la tasa de reproducción efectiva.
Efecto de las vacunas
Una de las recomendaciones anteriores era la vacunación, medida que reduce el número inicial de susceptibles y convierte la tasa de reproducción efectiva en a(1-p)/b , donde p es la fracción vacunada de la población total, teniéndose en cuenta también la efectividad de la vacuna. Por ejemplo, si el 70 % de la población está vacunado y la vacuna tiene una efectividad del 90 %, tendremos que p=0,63. Como normalmente no se puede vacunar a toda la población, y además la efectividad no suele ser del 100 %, tenemos que p < 1.
Por lo tanto, dependiendo de los valores de los parámetros a y b, se puede calcular qué proporción de la población se debe vacunar para evitar (o frenar considerablemente) la propagación de la infección. El objetivo es que el número de susceptibles se mantenga desde el principio por debajo del valor umbral mencionado más arriba. Cuando esto se consigue, se dice que se ha logrado la inmunidad comunitaria. La inmunidad comunitaria protege también a quienes no se han vacunado, incluidas, por supuesto, las personas contrarias a las vacunas. Sin embargo, si una parte significativa de la población se opone a las vacunas, se pierde la oportunidad de lograr la inmunidad comunitaria desde el principio.
Otros modelos
Como dijo el estadístico británico George Box, «todos los modelos se equivocan, pero algunos son útiles». Los modelos simplifican mucho la realidad, por lo que siempre habrá diferencia entre lo que prevén las matemáticas y lo que ocurre realmente. No obstante, lo más importante es la utilidad de la que hablaba Box. Algunos trabajos han demostrado que el modelo SIR, en su simplicidad, se ajusta bien a algunas epidemias. En cualquier caso, este ajuste puede ser más fácil a posteriori, una vez que se controlan mejor los parámetros de las ecuaciones.
Sea como fuere, el SIR no es el único modelo, y a veces se recurre a versiones más desarrolladas del mismo. De entre las que no incluyen grupos nuevos, se pueden mencionar las siguientes:
- El que tiene en cuenta la dinámica vital: los nacimientos se incluyen en el grupo S; en todos los grupos se dan fallecimientos por causas distintas a la infección.
- Modelo SIS: no hay inmunidad. Las personas infectadas que se recuperan pasan de nuevo al grupo S.
- Modelo SIRS: la inmunidad es temporal. Del grupo R se pasa de nuevo al S, pero no inmediatamente.
En otros modelos se añaden uno o más grupos nuevos, como, por ejemplo:
- E (exposed): personas en fase de incubación. Están infectadas, pero aún no transmiten la enfermedad.
- M (maternally derived immunity): las criaturas recién nacidas tienen inmunidad temporal, gracias a los anticuerpos de la madre.
- D (deceased): personas fallecidas por la infección. Estas salen del grupo R, donde quedan quienes sobreviven a la enfermedad.
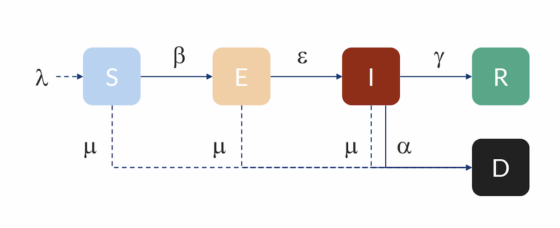
Tendiendo esto en cuenta, se han propuesto modelos como SEIR, SEIS, MSIR, SIRD, SEIRD, MSEIR, MSEIRS, etc., cuyas denominaciones reflejan claramente los grupos que incluyen y la forma en que se pasa de un grupo a otro. En estos casos harán falta más ecuaciones y parámetros.
Para saber más:
En la red se puede encontrar abundante información sobre el tema. Estas son algunas de las fuentes que se pueden consultar:
- Ridenhour, Benjamin, Kowalik, Jessica M. y Shay, David K. (2018). El número reproductivo básico (R0): consideraciones para su aplicación en la salud pública. American Journal of Public Health, 108(S6), S455_S465. DOI: https://doi.org/10.2105/AJPH.2013.301704s
- Weiss, Howard (2013). The SIR model and the Foundations of Public Health. Materials matemàtics, 2013(0), 1-17.
- Hethcote, Herbert W. (2000). The mathematics of infectious diseases. SIAM Review, 42(4), 599-653.
- Artículo sobre la Covid-19: Ed Fontes, Modeling the Spread of COVID-19 with COMSOL Multiphysics, COMSOL blog, 07-04-2020.
- Artículo de la Wikipedia en inglés: Compartmental models in epidemiology.
Sobre el autor: Javier Duoandikoetxea es catedrático de Análisis Matemático en la UPV/EHU.
Este artículo se publicó originalmente en euskara el 16 de junio de 2020 en el blog Zientzia Kaiera. Artículo original.
Pablo Rodríguez
Hace unos meses publicamos en Naukas un artículo relacionado (https://fuga.naukas.com/2020/03/18/un-matematico-en-cuarentena/), incluyendo una versión interactiva del modelo SIR (https://pabrod.shinyapps.io/SIRmodel/) que podría ser interesante para los lectores de este artículo.
Mapas de riesgo colaborativos mediante consenso: La Gomera – Miguel Rebollo
[…] modelar la propagación del SARS-CoV-2 se emplea un modelo SEIR sobre una población N=21.555 (la población de La Gomera) y con 300 personas infectadas […]
Epidemiología Computacional – OuArNSc
[…] https://culturacientifica.com/2020/08/24/el-modelo-sir-un-enfoque-matematico-de-la-propagacion-de-in…; […]