Hace más de 2.000 años que el ser humano tiene conocimiento de ese extraño fenómeno que es el magnetismo. Desde la antigua Grecia hasta la actualidad, la comunidad investigadora ha ido profundizando en los principios fundamentales de los imanes. Hace más de 100 años que se sabe que el magnetismo surge en los materiales en estado sólido cuando, debido a interacciones electrónicas y químicas, los espines de los electrones y su movimiento alrededor de los átomos adquieren una determinada disposición dentro del material. Desde este descubrimiento, los investigadores han desarrollado una amplia gama de mecanismos teóricos y experimentales para predecir y caracterizar los materiales magnéticos.

A pesar del intenso esfuerzo realizado por múltiples modelos (algunos de ellos premiados con el Nobel) que han intentado lograr una descripción unificada de las estructuras magnéticas de los materiales, esta ha permanecido sorprendentemente esquiva. De hecho, incluso el sistema de clasificación de materiales magnéticos con más éxito, desarrollado hace casi 75 años por el científico soviético Lev Shubnikov, estaba incompleto. Hasta ahora.

Un equipo de investigación internacional ha anunciado esta semana que por fin ha completado la caracterización matemática de los grupos de simetría de cristales magnéticos y no magnéticos de Shubnikov.

Un largo camino para llegar hasta aquí

Una de las primeras descripciones del magnetismo que tuvo la aceptación de muchos investigadores fue el modelo de representación, que ofrece una imagen simplificada en la que se ignora gran parte de la estructura del material subyacente, y el magnetismo se describe a través de la repetición de ondas espín electrónico parcialmente desacopladas del resto del material. Desde los años 50, las limitaciones de esta teoría de la representación han sido evidentes. De hecho, el modelo se desmorona cuando se tienen en cuenta las interacciones realistas más simples entre los espines de los electrones y los átomos subyacentes.

Shubnikov, en cambio, al clasificar los materiales por su geometría, tuvo en cuenta todas las complicadas simetrías de los cristales y, a continuación, consideró las formas aún más complicadas en que esas simetrías pueden reducirse mediante el ordenamiento magnético. El sistema de Shubnikov permite clasificar todos los cristales posibles —magnéticos o no— por alguna de las 1.651 colecciones de simetrías conocidas como grupos espaciales magnéticos y no magnéticos.

Hace más de 50 años que se conocen las propiedades matemáticas completas de 230 grupos espaciales de Shubnikov, conocidas como coreps (del inglés ‘small corepresentations’). Pero en el caso de los grupos espaciales magnéticos, las coreps han permanecido en gran medida sin identificar e inaccesibles, debido a las complicadas simetrías de los cristales magnéticos y al gran número de grupos espaciales magnéticos.

En el presente estudio, el equipo ha calculado minuciosamente los más de 100.000 pequeñas coreps de los grupos espaciales magnéticos mediante una serie de cálculos redundantes para garantizar la coherencia interna.

Bases de datos de acceso abierto

Basándose en los resultados del equipo, Luis Elcoro, profesor de la Universidad del País Vasco y uno de los autores principales del estudio, escribió un código informático para generar un amplio conjunto de recursos disponibles públicamente en el Bilbao Crystallographic Server, lo que permite a personal investigador de todo el mundo acceder a los datos resultantes del equipo.

Elcoro comenta: «Las comunidades científicas de cristalografía y estructura magnética han estado esperando una guía accesible y completa de las coreps magnéticas desde antes de que yo naciera. Ahora se puede caracterizar de forma robusta todas las posibles transiciones de fase magnética en estudios experimentales de materiales magnéticos —que suelen realizarse mediante experimentos de difracción de neutrones— sin tener que recurrir a métodos incompletos de teoría la de representaciones.»

Aplicaciones cuánticas

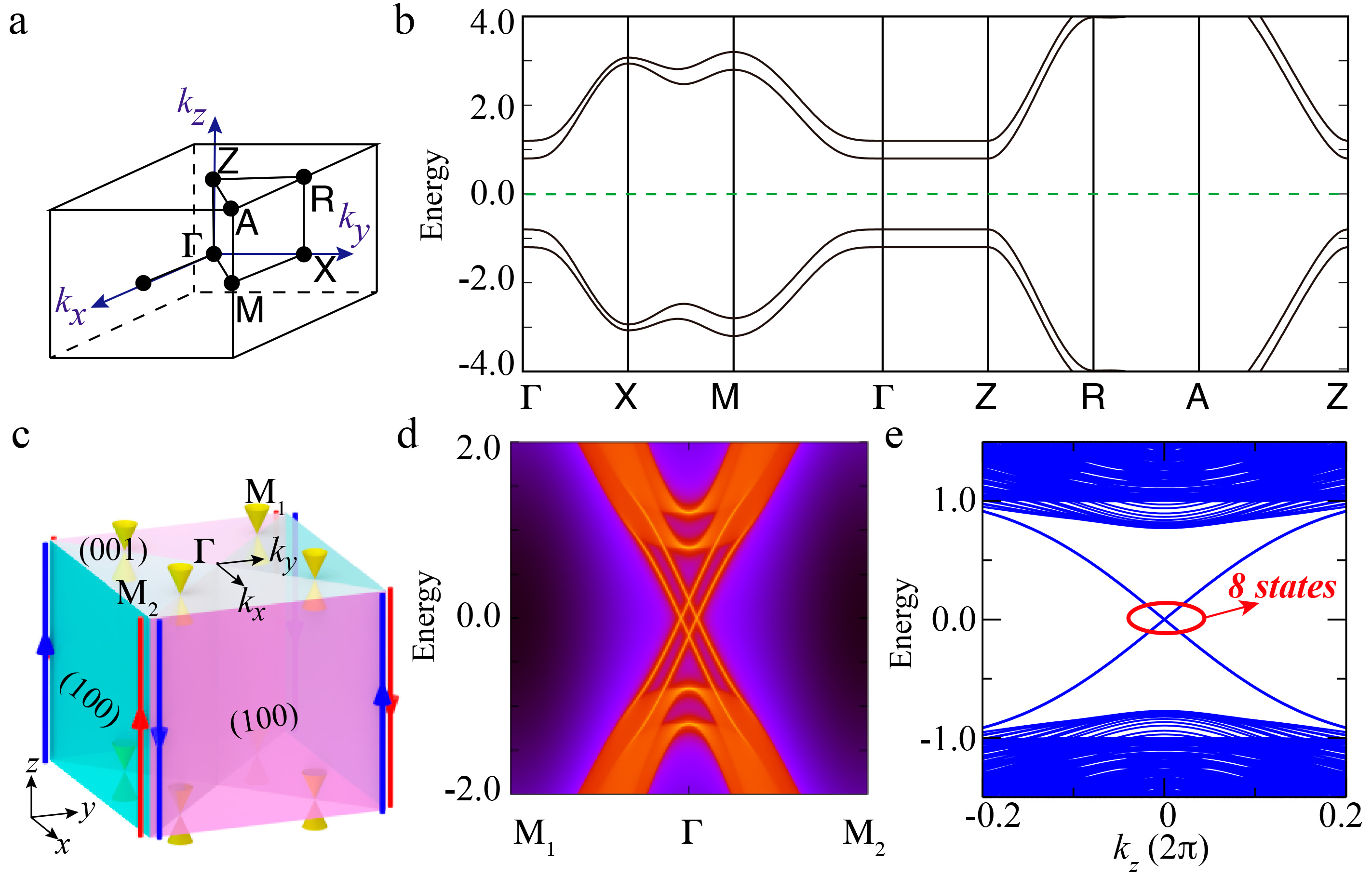
Consciente de la conexión matemática entre las coreps y la estructura electrónica de los materiales de estado sólido, el equipo realizó posteriormente cálculos adicionales para relacionar los datos de simetría magnética resultantes con aislantes y semimetales de banda topológica (estados electrónicos exóticos con descripciones matemáticas increíblemente intrincadas). Estos estados son prometedores para aplicaciones cuánticas como, por ejemplo, plataformas para la ingeniería de la información cuántica y dispositivos espintrónicos cuánticos.

Benjamin Wieder, investigador postdoctoral en el MIT y de la Northeastern University y otro de los autores principales del trabajo, estudió a fondo las herramientas de simetría de Elcoro para deducir la clasificación exhaustiva de los aislantes topológicos magnéticos, utilizando una mezcla de teoría matemática y cálculos manuales de fuerza bruta.

«Durante las vacaciones de 2019, enviaba cada día por correo electrónico a Elcoro mi intento de clasificación de un par de grupos espaciales magnéticos», recuerda Wieder. «Pasé la mayor parte de esas vacaciones garabateando borradores de la clasificación entre las comidas y el postre, para desconcierto de mis amigos y familiares».

Química cuántica topológica magnética

En colaboración con Barry Bradlyn, profesor de física de la Universidad de Illinois en Urbana-Champaign, el trabajo de Elcoro y Wieder se combinó entonces en una nueva teoría, que denominaron Química Cuántica Topológica Magnética (MTQC por sus siglas en inglés). La MTQC es capaz de caracterizar todas las bandas electrónicas topológicas posibles en función de su química en el espacio de posiciones y orden magnético. La MTQC toma las posiciones y tipos de átomos en el cristal, así como la orientación magnética, y da como resultado el conjunto de características topológicas permitidas. Las bases de la MTQC fueron presentadas hace cuatro años por miembros de este mismo grupo de colaboración en un trascendental artículo titulado Topological Quantum Chemistry.

Bradlyn, que fue el autor principal del artículo original sobre Química Cuántica Topológica, señala que «la MTQC responde a algunas de las mayores cuestiones pendientes planteadas por nuestro trabajo anterior. Si quisiéramos considerar el magnetismo en un material topológico, antes habríamos tenido que empezar de cero cada vez. Aplicando las mismas herramientas en el espacio de posiciones que desarrollamos para la Química Cuántica Topológica, ahora tenemos una comprensión unificada de los aislantes topológicos en materiales magnéticos y no magnéticos.»

Simulación de materiales por métodos numéricos

A partir de los cálculos de Elcoro y Wieder, el equipo recurrió a Zhida Song y Yuanfeng Xu para conectar la MTQC con diagnósticos numéricos eficaces de simetría y topología de materiales magnéticos reales.

Song, investigador postdoctoral de la Universidad de Princeton, es conocido por su trabajo anterior sobre métodos numéricos para la identificación de aislantes topológicos en el cálculo de materiales. Para este estudio, Song realizó cálculos teóricos para relacionar la clasificación de Wieder con los trabajos anteriores de Song sobre materiales no magnéticos.

Song resume el resultado de los múltiples esfuerzos del equipo: «Cuando el polvo se asentó, nos encontramos ante la primera guía universal de aislantes topológicos magnéticos en materiales reales».

En la fase final de este estudio, Xu, investigador postdoctoral del Instituto Max Planck de Física de Microestructuras, realizó simulaciones numéricas a gran escala de modelos teóricos y materiales magnéticos reales para validar la teoría subyacente. Además de su trabajo en el presente trabajo, Xu fue el autor principal de un estudio publicado en Nature el año pasado, en el que Xu y otros investigadores aplicaron la MTQC para realizar la primera búsqueda sistemática de materiales magnéticos topológicos.

Andrei Bernevig, profesor de la Universidad de Princeton, investigador Ikerbasque en el DIPC y principal investigador de ambos trabajos, destaca que «la MTQC representa un intenso estudio en colaboración durante más de cuatro años».

Dado que los dos últimos años de colaboración y redacción de los dos trabajos —que suman más de 400 páginas— se realizaron a distancia durante la pandemia de la Covid-19, Bernevig concluye que «este es un ejemplo de la dedicación y la concentración sobrenatural de nuestro equipo, que fue capaz de persistir y completar este problema tan antiguo».

Referencia:

Luis Elcoro, Benjamin J. Wieder, Zhida Song, Yuanfeng Xu, Barry Bradlyn, B. Andrei Bernevig (2021) Magnetic topological quantum chemistry Nature Communications doi: 10.1038/s41467-021-26241-8

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa