Un número que desaparece
Un número que desaparece
Puede ser muy difícil definir la belleza matemática, pero eso es cierto para la belleza de cualquier tipo. Puede que no sepamos muy bien a qué nos referimos con un hermoso poema, pero eso no impide que reconozcamos uno cuando lo leemos.
Ruth Minnen en «A Disappearing Number»

A Disappearing Number (Un número que desaparece) es el título de una obra de teatro estrenada en el año 2007 por la compañía Complicité y dirigida por el dramaturgo británico Simon McBurney. La trama se inspira, en parte, en el ensayo Apología de un matemático de Godfrey Harold Hardy, y trata sobre la colaboración de este científico británico con el matemático indio Srinivasa Ramanujan.
La obra trata también sobre la pasión que provocan las matemáticas a las personas que se dedican a ellas.
Un matemático, como un pintor o un poeta, es un creador de patrones. Si sus patrones son más que permanentes que los del poeta, es porque están hechos de ideas. […] Los patrones de un matemático, como los de un pintor o un poeta, deben ser hermosos; las ideas, como los colores o las palabras, deben encajar de una manera armoniosa. La belleza es la primera prueba; no hay lugar permanente en el mundo para unas matemáticas feas.
Godfrey Harold Hardy
El prólogo del libreto, titulado A most romantic collaboration (Una colaboración de lo más romántica), está escrito por el matemático Marcus du Sautoy. En él explica que, en enero de 1913, Hardy recibió una extraña carta procedente de la India que contenía extraordinarios teoremas matemáticos. El remitente de esa misiva era Srinivasa Ramanujan, que consiguió atraer la atención de Hardy con su demostración de la fórmula:
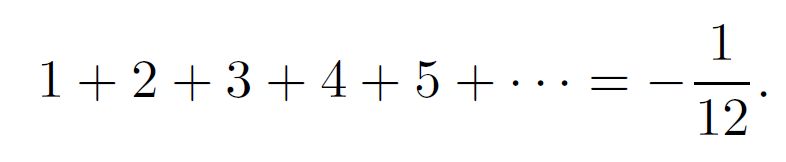
Du Sautoy cita también la última carta que Ramanujan envío a Hardy el 12 de enero de 1920. En ella hablaba de una idea matemática realmente adelantada a su época y que llamó función theta simulada. En esa misiva daba algunos ejemplos de este tipo de función; posteriormente se descubrieron más en su cuaderno perdido. Como recuerda Du Sautoy, en el año 2006, los especialistas en teoría de números Kathrin Bringmann y Ken Ono dieron la primera explicación completa de las ideas contenidas en esta carta.
En la obra de teatro, por supuesto, se mencionan ambas cartas. También se alude al famoso número taxicab (1729), la teoría de particiones en la que Hardy y Ramanujan trabajaron, los diferentes tipos de infinito o la manera de hacer una demostración.
Dos historias que se cruzan
A Disappearing Number tiene dos hilos narrativos que se entrelazan: la compleja y apasionada relación personal e intelectual entre Hardy y Ramanujan (entre 1913 y 1919) se cruza con la historia contemporánea de la matemática Ruth Minnen y su marido Al Cooper, un hombre de negocios indio-estadounidense.
En 1914, Ramanujan viajó de la India a Inglaterra para trabajar con Hardy. Y, cien años más tarde, Ruth viaja a la India siguiendo los pasos de Ramanujan, cuyas matemáticas estudia, y buscando inspiración.
La obra comienza precisamente con una clase de Ruth que explica a sus estudiantes el famoso sumatorio de Ramanujan, técnica inventada por el matemático y que asigna “una suma” a una serie divergente. Como hemos comentado al principio, en la carta de 1913 de Ramanujan a Hardy había un ejemplo de este tipo de sumatorio.
Al Cooper entra por error en el aula en la que Ruth imparte su lección y, a pesar de que no comprende el contenido de lo que aparece en la pizarra, regresa al día siguiente para conocer mejor a la matemática. Finalmente, se enamoran y se casan.
La matemática estudia el trabajo de Ramanujan. A veces se siente frustrada porque Al no comprende su pasión por las matemáticas. Su marido no entiende, por ejemplo, por qué el número de teléfono de Ruth (el 1729) es especial para ella. Él viaja continuamente por su trabajo. Pero será el viaje de Ruth a la India en busca de inspiración el que les separará definitivamente: ella fallece allí de un aneurisma cerebral.
La colaboración entre Ramanujan y Hardy puede recordarse en Particiones: Hardy y Ramanujan: en A Disappearing Number también se presentan esa primera carta, la profunda admiración mutua que sentían, sus diferentes maneras de trabajar o su distanciamiento final.
Es una lástima no haber podido asistir a una representación de la obra para apreciar todos los detalles que el libreto no puede transmitir. Con la simple lectura, lo que se evidencia, sin duda, es la pasión por la investigación matemática de los personajes. Así se muestra en esta cita de Ruth, casi al final de la obra, cuando se anuncia su muerte y, unos cien años antes, la de su admirado Ramanujan.
Para mí, y supongo que, para la mayoría de los matemáticos, hay otra realidad, que llamaré la realidad matemática. […] Pero el número 2 o el 317 no tienen nada que ver con sensaciones. 317 es un número primo, no porque yo lo piense, o porque nuestras mentes están formadas de una manera en lugar de otra, sino porque es así, porque la realidad matemática está construida de esta manera.
Ruth Minnen en «A Disappearing Number»
Referencias
-
Complicité, A disapearing number, Oberon books, 2009
-
Liliane Campos. Searching for resonance: scientific patterns in Complicite’s Mnemonic and A Disappearing Number. Interdisciplinary Science Reviews 32 (4), (2007) 326-334
-
Rachel Thomas, A disappearing number, Plus Magazine, diciembre 2008
-
Marta Macho Stadler, Particiones: Hardy y Ramanujan, Cuaderno de Cultura Científica, 14 de agosto de 2019
-
Marta Macho Stadler, Un retrato alfabético de Srinivasa Ramanujan, Cuaderno de Cultura Científica, 22 de diciembre de 2021
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad