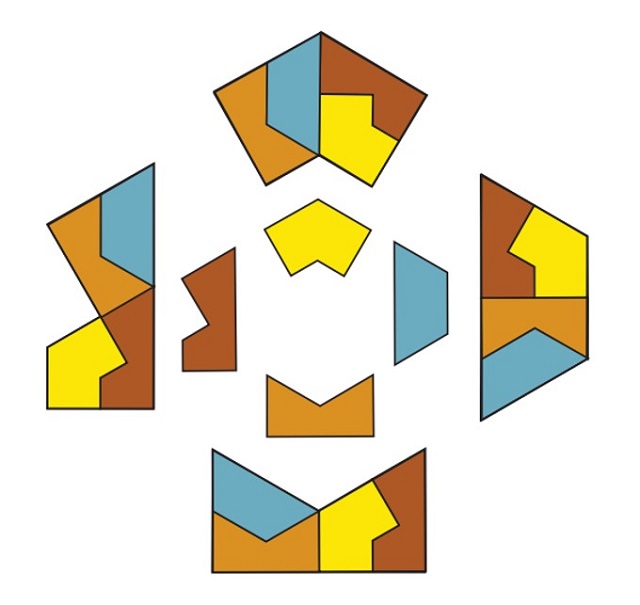
Conjuntos de baldosas auto-embaldosadas
auto-embaldosadas
En la anterior entrada del Cuaderno de Cultura Científica titulada Los reptiles geométricos estuvimos hablando de un interesante tipo de figuras geométricas conocidas con el nombre de repiteselas, o reptiles geométricos.

Una repitesela, o reptil geométrico, si jugamos con el término en inglés con el que bautizó a estos objetos geométricos el matemático e ingeniero estadounidense Solomon W. Golomb, es una forma geométrica plana (poligonal) que puede ser diseccionada en copias idénticas de ella misma, como en el anterior ejemplo en el que la figura de la «esfinge» se descompone en cuatro copias (lo que se conoce como el orden de la repitesela) de sí misma. Recordemos también que el nombre de “rep-tiles” (repiteselas) viene de la expresión “self-replicating tiles” (teselas o baldosas auto-replicantes), haciendo un gracioso juego de palabras con el grupo de animales que reciben el nombre de reptiles.

El ingeniero electrónico británico, apasionado de la matemática recreativa, Lee C. F. Sallows (1944), generalizó el concepto de repiteselas, es decir, teselas o baldosas auto-replicantes, al concepto de “conjunto de baldosas auto-embaldosadas” (self-tiling tile sets, en inglés, que acorta a “setiset”) o también podemos traducirlo como “conjunto de teselas auto-teseladas”.
Cuadrados mágicos geométricos
Antes de entrar en la definición y ejemplos de ese nuevo concepto, recordemos que Lee Sallows fue quien introdujo el concepto de cuadrado mágico geométrico sobre el que ya hemos escrito en el Cuaderno de Cultura Científica, en concreto, en la entrada Cuadrados mágicos geométricos. Como el concepto de conjunto de baldosas auto-embaldosadas tiene elementos de conexión con el de cuadrado mágico geométrico, vamos a recordar en qué consiste este (para el caso sencillo del orden 3) y mostrar un par de ejemplos.
Un cuadrado mágico geométrico (también llamado cuadrado geomágico) de orden 3 está formando por una cuadrícula 3 x 3 de formas geométricas tales que se pueden unir las formas de cada fila, cada columna o cada diagonal principal para formar la misma figura geométrica, llamada forma objetivo.
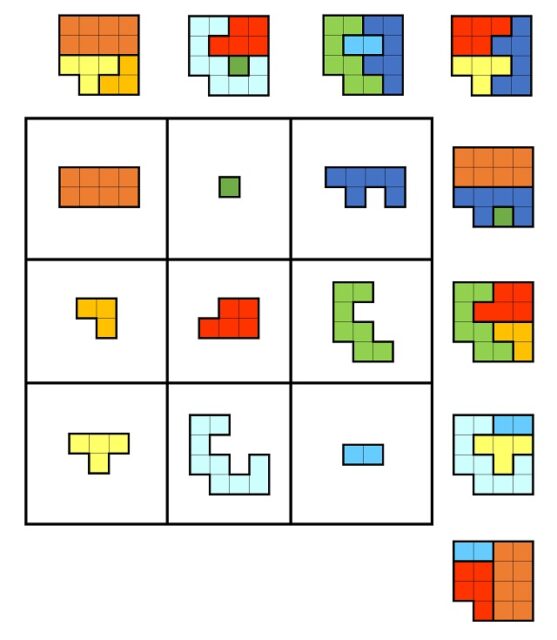
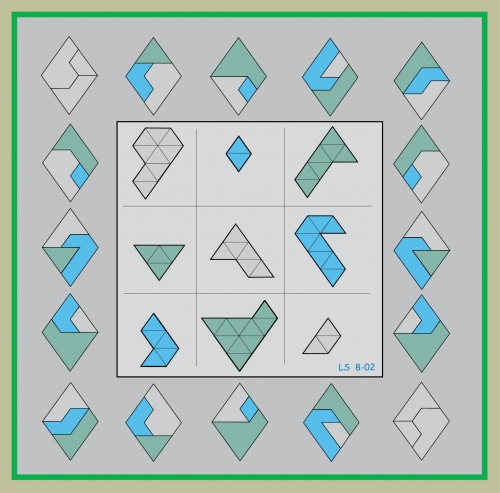
En el ejemplo anterior las nueve formas geométricas de la retícula 3 x 3 son poliominós, es decir, figuras geométricas planas formadas conectando dos o más cuadrados por alguno de sus lados (para más información sobre los poliominós se pueden leer las entradas Embaldosando con L-triominós (Un ejemplo de demostración por inducción) y Tetris, embaldosados y demostraciones). Sin embargo, las figuras geométricas de la retícula pueden ser otro tipo de poliformas, como los polidiamantes, que son como los poliominós pero con triángulos equiláteros en lugar de cuadrados (un ejemplo de cuadrado geomágico con polidiamantes se muestra en la siguiente imagen) o formas más generales (ejemplos pueden verse en la entrada Cuadrados mágicos geométricos o en la página web Geomagic squares de Lee Sallows).
Conjuntos de baldosas auto-embaldosadas
En el artículo On Self-Tiling Tile Sets (Sobre conjuntos de teselas auto-teseladas), publicado en la revista Mathematics Magazine, su autor, Lee Sallows, define los conjuntos de baldosas auto-embaldosadas de la siguiente forma.
Un conjunto de baldosas auto-embaldosadas de orden n es un conjunto de n formas geométricas planas distintas (no similares), que pueden ser diseccionadas en copias idénticas de ellas mismas o, equivalentemente, que pueden unirse para formar una copia más grande de cada una de ellas.
El primer ejemplo con el que su autor ilustra este nuevo concepto es el siguiente conjunto de baldosas auto-embaldosadas de orden 4 formado por poliominós, en concreto, por cuatro hexominós.
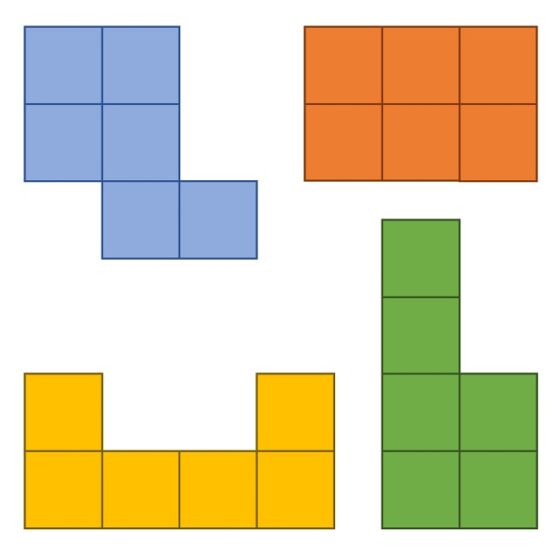
En la siguiente imagen se muestra como estos cuatro hexominós pueden unirse para formar una copia más grande de cada uno de ellos, luego son un conjunto de baldosas auto-embaldosadas de orden 4.

Un ejemplo de conjunto de baldosas auto-embaldosadas de orden 2
En ese primer artículo, On Self-Tiling Tile Sets (Sobre conjuntos de teselas auto-teseladas), Sallows se plantea buscar un ejemplo de conjunto de baldosas auto-embaldosadas de orden 2, es decir, formado por dos formas geométricas. En concreto, busca ejemplos en los que las figuras geométricas sean triángulos, lo cual motiva que además las dos piezas (que son los dos triángulos) se puedan unir por un vértice “bisagra” que permite transformar uno de los triángulos en el otro (iguales a las dos piezas originales pero más grandes) girando las piezas alrededor de la bisagra.
Sallows construye una familia de conjuntos de baldosas auto-embaldosadas de orden 2 formada por parejas de triángulos, que pueden verse en la siguiente imagen.
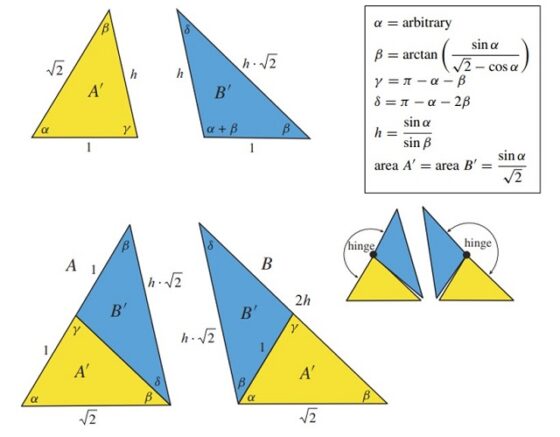
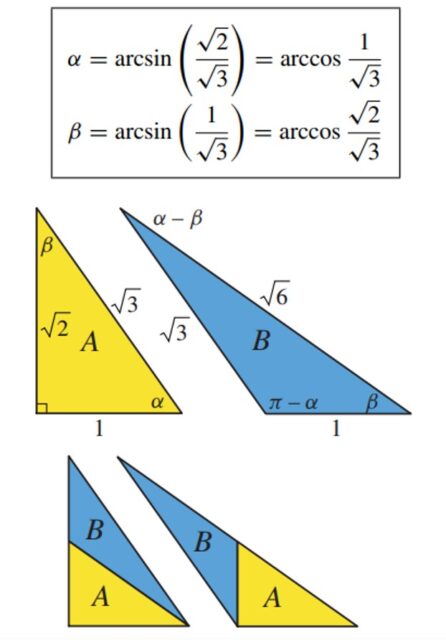
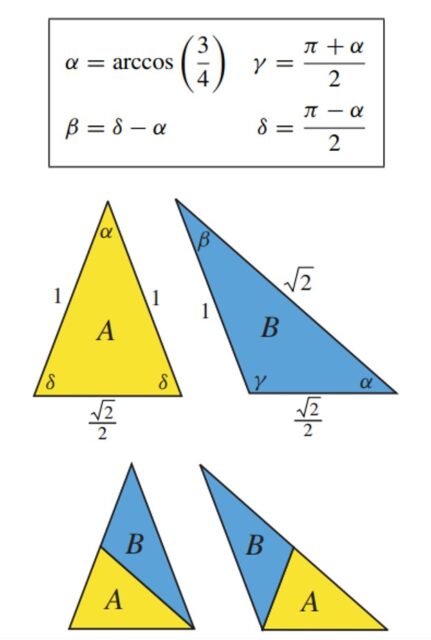
Dentro de esa familia se pueden considerar dos casos interesantes, cuando uno de los triángulos (el triángulo A en la imagen) es un triángulo rectángulo o un triángulo isósceles, que mostramos en las siguientes imágenes.
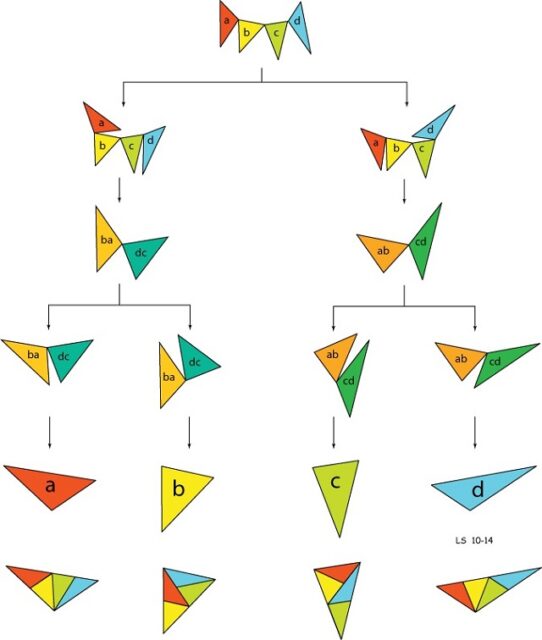
Tras la construcción de estos ejemplos, Lee Sallows va más allá, como podemos leer en su página web, en la parte dedicada a los conjuntos de baldosas auto-embaldosadas (Self-Tiling Tile Sets). Este ingeniero electrónico, apasionado de la matemática recreativa, construye un conjunto de baldosas auto-embaldosadas de orden 4, formado por cuatro triángulos conectados con bisagras, de manera que los dos primeros y los dos últimos forman dos conjuntos de baldosas auto-embaldosadas de orden 2, que se muestra en la siguiente imagen.
Más ejemplos de conjunto de baldosas auto-embaldosadas
Vamos a terminar esta entrada del Cuaderno de Cultura Científica con algunos ejemplos más de conjuntos de baldosas auto-embaldosadas de diferentes órdenes. El primer ejemplo es un ejemplo del artículo More On Self-Tiling Tile Sets (Más sobre conjuntos de teselas auto-teseladas) y es un conjunto de baldosas auto-embaldosadas de orden 4, formado por cuatro piezas geométricas que no son ni triángulos, ni poliformas (poliominós, poliodiamantes u otras).
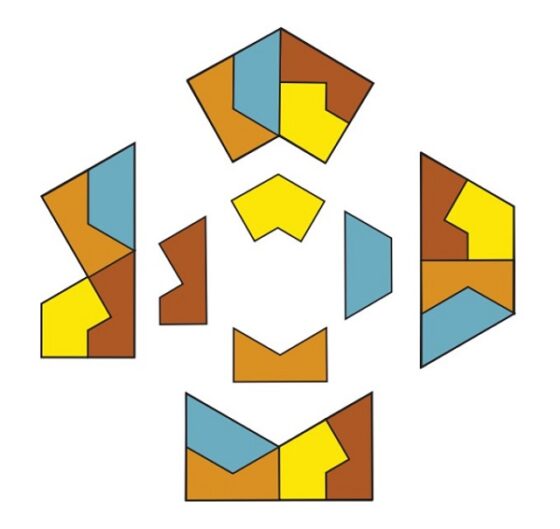
En el artículo More On Self-Tiling Tile Sets (Más sobre conjuntos de teselas auto-teseladas) Sallows nos muestra que se pueden obtener conjuntos de baldosas auto-embaldosadas a partir de las repiteselas. El siguiente ejemplo es un conjunto de baldosas auto-embaldosadas de orden 4, construido a partir del reptil geométrico “esfinge”, con el que iniciábamos esta entrada. Lo primero que hace es diseccionar la figura de la esfinge (formada por cuatro copias de ella misma), en tres parejas de figuras geométricas planas, que mostramos a continuación.
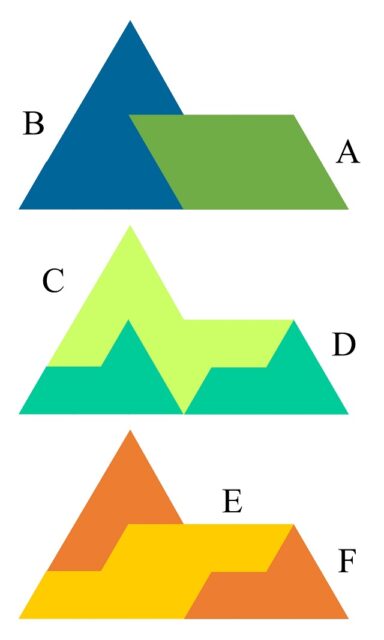
De donde, las cuatro figuras geométricas planas A, B, C, D forman un conjunto de baldosas auto-embaldosadas de orden 4, como se muestra a continuación.

Lo mismo ocurre para los dos grupos de cuatro figuras geométricas planas A, B, E, F y C, D, E, F.
Este tipo de construcción podemos realizarla para otras repiteselas. Terminemos con un el ejemplo del triángulo rectángulo isósceles, que es un sencillo reptil geométrico de orden 4.

A partir de aquí podemos realizar dos disecciones del triángulo rectángulo isósceles como unión de cuatro pequeños triángulos rectángulos isósceles (la tercera pareja posible es igual a una de ellas, por eso no la incluimos).

Y efectivamente, podemos comprobar que, a partir de esas cuatro figuras geométricas, obtenidas como disecciones del triángulo rectángulo isósceles, podemos unirlas formando una copia más grande de cada una de ellas, como se muestra en la siguiente imagen.

Bibliografía
1.- Charles Dudley Langford, Uses of a Geometric Puzzle, The Mathematical Gazette 24 (260), pp. 209–211, 1940.
2.- Solomon W. Golomb, Replicating figures in the plane, The Mathematical Gazette 48 (366), pp- 403–412, 1964.
3.- Martin Gardner, The Unexpected Hanging and Other Mathematical Diversions (capítulo 19: Rep-Tiles, Replicating Figures on the Plane), Chicago University Press, 1991.
4.- Lee C. F. Sallows, On Self-Tiling Tile Sets, Mathematics Magazine Vol. 85, No. 5, pp. 323–333, 2012.
5.- Lee C. F. Sallows, More On Self-Tiling Tile Sets, Mathematics Magazine, Vol. 87, No. 2, pp. 100–112, 2014.
6.- Página web de Lee Sallows
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica