La guerra es una masacre entre gentes que no se conocen, para provecho de gentes que sí se conocen pero que no se masacran.

Paul Valéry

Se conocen como leyes de Lanchester a unas ecuaciones diferenciales que buscan describir los conflictos entre dos fuerzas enemigas.

En 1902, el entonces teniente de la Marina de los Estados Unidos Jehu V. Chase desarrolló una ecuación diferencial para intentar describir los combates entre dos flotas homogéneas. Hasta 1972 no se desclasificó el trabajo de Chase, con lo que no recibió el reconocimiento por esta aportación temprana.

En 1916, el ingeniero británico Frederick Lanchester llegó de forma independiente a ecuaciones casi idénticas a las de Chase, con ejemplos que incorporaban también los conflictos aéreos y terrestres.

Un militar ruso contemporáneo de ambos, M. Osipov, también llegó a conclusiones similares a las de Chase y Lanchester en un artículo publicado en una revista militar rusa en 1915.

La ley lineal de Lanchester

Lanchester argumentaba que, en las guerras antiguas, cada soldado se enfrentaba a un único enemigo a la vez. Suponía que cada soldado mataba o era asesinado por exactamente un soldado del ejército contrario, por lo que el número de sujetos que sobrevivían a una batalla era sencillamente la diferencia (en valor absoluto) de tamaño entre los dos ejércitos. Esta se conoce como la ley lineal de Lanchester.

La ley cuadrática de Lanchester

La ley cuadrática de Lanchester modeliza el combate moderno que se realiza con armas de largo alcance como las armas de fuego. Y aquí las cosas cambian. Las armas de fuego se enfrentan con disparos controlados a distancia; se pueden atacar a diferentes objetivos y recibir impactos desde varios lugares. La tasa de desgaste (efectividad que cada fuerza en contienda posee a la hora eliminar a sus enemigos) depende en este contexto solo del número de armas en juego. Lanchester determinó que el poder de tal fuerza es proporcional al cuadrado de las unidades puestas en juego, no al número de ellas.

Para comprenderlo mejor, supongamos que tenemos dos ejércitos A y B que se enfrentan en combate. A dispara un flujo continuo de balas a B mientras que B actúa exactamente de la misma manera con A.

Vamos a denotar por a al número de soldados de la fuerza A y por α la potencia de fuego ofensiva de cada soldado, es decir, el número de soldados enemigos que puede incapacitar (herir o matar) por unidad de tiempo. Del mismo modo, denotamos por b al número de soldados de B, cada uno con potencia de fuego ofensiva β.

La ley cuadrática de Lanchester estima el número de soldados perdidos en cada bando usando el par de ecuaciones siguientes:

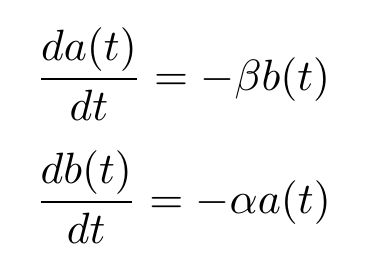
En estas ecuaciones da(t)/dt representa la velocidad a la que cambia el número de soldados de A en un instante dado; un valor negativo indicaría la pérdida de soldados. De manera similar, db(t)/dt representa la tasa de cambio del número de soldados del ejército B. Intuitivamente, este sistema de ecuaciones indica que el número de soldados de cada ejército disminuye de manera proporcional al número de soldados enemigos.

La solución de estas ecuaciones muestra que:

Si α = β, es decir, si ambos bandos poseen la misma potencia de fuego, entonces gana aquel que tiene más soldados al comienzo de la batalla.

Si a = b, es decir, si los dos ejércitos tienen el mismo número de soldados, vence el bando con mayor potencia de fuego.

Si a > b y α > β, entonces triunfa el bando A (del mismo modo, si a < b y α < β, gana el ejército B).

Las anteriores conclusiones son obvias. Queda un último caso, que es la llamada ley cuadrática. Corresponde a la situación en la que la cantidad de soldados y la potencia de fuego son desiguales en direcciones opuestas. Es decir, si a > b y α < β (o si a < b pero α > β) el ejército que resulta ganador depende de si la relación β / α es mayor o menor que el cuadrado de la relación a / b. Así, para ganar la contienda, se requiere una superioridad en potencia de fuego igual al cuadrado de la inferioridad en número. De otro modo, la eficacia de un ejército aumenta proporcionalmente al cuadrado del número de personas que lo componen, pero sólo linealmente con su capacidad de lucha.

¿Para qué se usan?

Las leyes de Lanchester se han usado para modelar batallas históricas con fines de investigación. Entre otras, se han estudiado la batalla de Inglaterra de 1940 que enfrentó a las fuerzas aéreas británica y alemana, o la batalla de Kursk de 1943 que se libró entre el ejército alemán y el soviético.

También se pueden utilizar estas leyes, por citar algún ejemplo, para modelizar el combate en juegos de estrategia en tiempo real o en mirmecología, para entender cómo se relacionan las especies endémicas y las invasoras.

De cualquier manera, independientemente de la eficacia de cualquier modelo matemático, como afirmaba la política estadounidense y defensora de los derechos de las mujeres Jeannette Rankin:

No se puede ganar una guerra como tampoco se puede ganar un terremoto.

Jeannette Rankin

Referencias

• Lanchester’s Laws, Futility Closet, 20 de marzo de 2016
• Lanchester’s laws, Wikipedia
• J.V. Chase (1902). Sea Fights: A Mathematical Investigation of the Effect of Superiority of Force in Combats upon the Sea. Naval War College Archives, RG 8, Box 109, XTAV.
• M. Osipov (1905). The influence of the numerical strength of engaged forces on their casualties, Originally Published in the Tzarist Russian Journal “Voennyi Sbornik” [Translation of September 1991 by Dr. Robert L. Heimbold and Dr. Allan S. Rehm]
• Frederick William Lanchester, Aircraft in Warfare: The Dawn of the Fourth Arm, Constable limited, 1916

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad