Mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Los sólidos platónicos, estaba dedicada a explicar qué son los poliedros regulares convexos, conocidos con el nombre de sólidos platónicos, quienes son (tetraedro, octaedro, icosaedro, cubo y dodecaedro), cuál es su origen y su relación con la cosmogonía platónica, así mismo, nos preguntamos si ya eran conocidos en el neolítico, como sugiere una conocida fotografía.

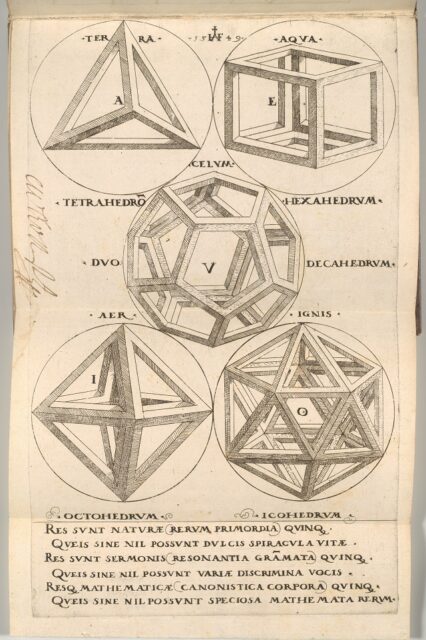
Como explicábamos en la anterior entrada, los sólidos platónicos son los poliedros regulares convexos. Por lo tanto, para empezar, son poliedros, es decir, figuras geométricas tridimensionales formadas por caras poligonales planas, aristas rectas (que son los lados compartidos de cualesquiera dos caras poligonales planas) y vértices (que son los puntos en los que se juntan las aristas).

Pero los sólidos platónicos son un tipo especial de poliedros, en particular, son poliedros regulares, es decir, sus caras son polígonos regulares (esto quiere decir que los lados del polígono, respectivamente, sus ángulos interiores, son iguales entre sí) todos iguales y la estructura de todos los vértices es la misma. Más aún, los sólidos platónicos son poliedros regulares que además son convexos. La convexidad, como se explicaba en la anterior entrada, de define de la siguiente forma. Un poliedro (o cualquier otro objeto geométrico) es convexo si dados dos puntos cualesquiera del mismo, el segmento que los une está en el interior del poliedro. Esta definición general tiene una expresión particular en el caso de los poliedros, ya que un poliedro es convexo si para el plano en el que se apoya cualquier cara de este, el poliedro estará colocado completamente a un solo lado de dicho plano.

Si se mira la anterior imagen, puede observarse que claramente los poliedros que en ella aparecen, el tetraedro, el cubo, el dodecaedro, el octaedro y el icosaedro, son poliedros regulares convexos, luego sólidos platónicos. En la entrada Los sólidos platónicos se explicaba, y se demostraba con un sencillo argumento que se remonta a la matemática griega, que solo existen estos cinco sólidos platónicos.

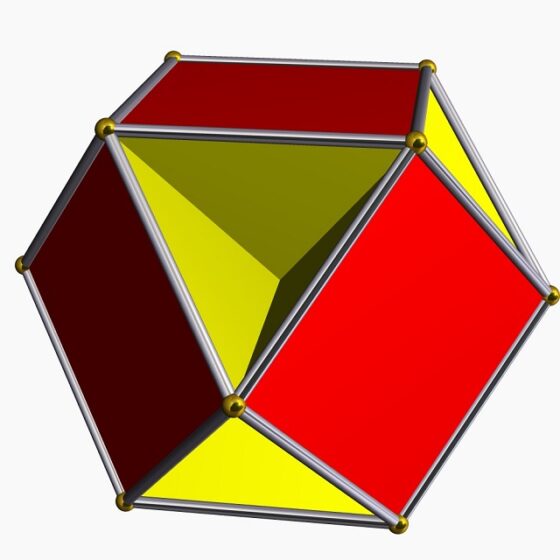
Sin embargo, en esta entrada nos vamos a plantear si existen poliedros regulares que no sean convexos. La no convexidad se puede manifestar de dos formas distintas. La primera es que las caras del poliedro se intersequen unas con otras, con lo cual claramente el poliedro no puede ser convexo, puesto que, al intersecarse las caras, el plano que contiene a cualquiera de ellas divide al poliedro es dos partes, una a cada lado del plano. Por ejemplo, en la siguiente imagen se muestra el cubohemioctaedro, un polígono no convexo, formado por 10 caras (6 de ellas son cuadrados y el resto hexágonos), 24 aristas y 12 vértices, en cada uno de los cuales confluyen dos cuadrados y dos hexágonos, que se intersecan entre sí.

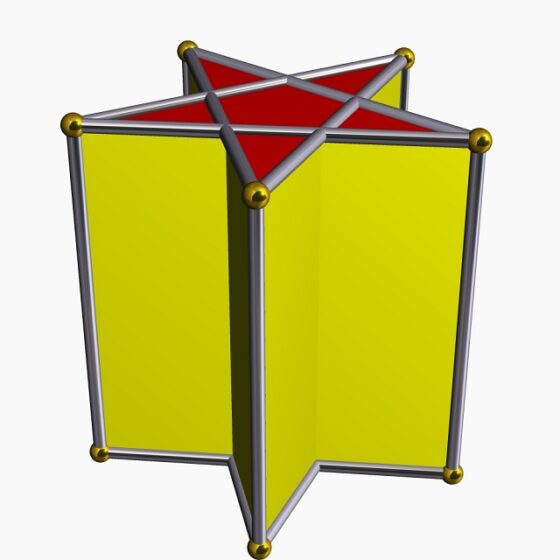
Este caso incluye que las propias caras poligonales pueden ser también estrelladas, en particular, que los lados del polígono se intersequen entre sí, como en el prisma pentagrámico, que es un poliedro no convexo formado por 7 caras (5 de ellas cuadrados y las otras 2 pentagramas o estrellas pentagonales, es decir, polígonos regulares formados por 5 vértices y 5 artistas, que no unen vértices consecutivos, sino que se van saltando uno), 15 aristas y 10 vértices.

La segunda manera en que un poliedro no es convexo es que las caras del poliedro no se intersequen unas con otras, pero aun así no se cumpla la propiedad de convexidad. Un ejemplo de esta situación nos lo encontramos en el icosaedro de Jensen, que es un poliedro no convexo, con la misma cantidad que el icosaedro regular de caras triangulares (20) -aunque aquí son 8 triángulos equiláteros y 12 triángulos isósceles-, aristas (30) y vértices (12). Claramente, como se ve en la imagen, en no convexo (en muchos de los casos, el segmento que une dos vértices no está dentro del poliedro).

Teniendo en cuenta que las caras de un poliedro regular son polígonos regulares, incluyendo los polígonos estrellados (no convexos), vamos a realizar un pequeño recorrido por estos.

Los polígonos regulares

Para empezar, recordemos que un polígono es una figura geométrica plana formada por vértices y segmentos (aristas) que forman una cadena poligonal (una secuencia alternada de vértices y segmentos, tal que tres vértices consecutivos no sean colineales) cerrada, es decir, que empieza y termina en el mismo vértice.

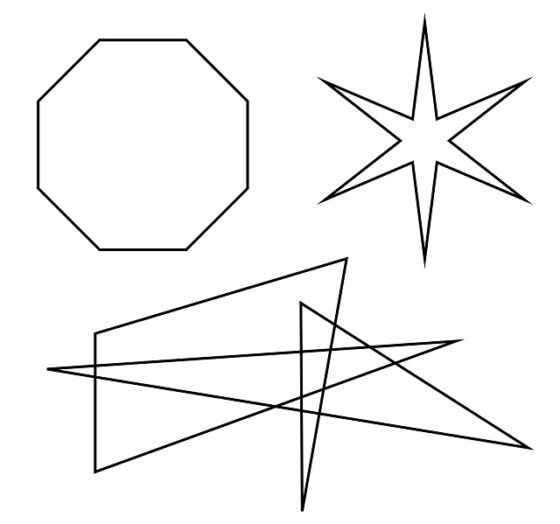
Por otra parte, las caras de los poliedros regulares son polígonos regulares, es decir, polígonos que tienen los lados y los ángulos iguales. Además, estos pueden ser convexos o no convexos.

Los polígonos regulares convexos son, como es de sobra conocido, el triángulo equilátero (3 lados/aristas y ángulo interior de 60 grados), el cuadrado (4 lados y ángulo interior de 90 grados), el pentágono (5 lados y ángulo de 108 grados), el hexágono (6 lados, 120 grados), el heptágono (7 lados, 128,57 grados), el octógono (8 lados, 135 grados), el nonágono (9 lados, 140 grados), el decágono (10, 144 grados), el endecágono (11 lados, 147,27 grados), el dodecágono (12 lados, 150 grados), y así vamos subiendo el número de lados, cada vez uno más.

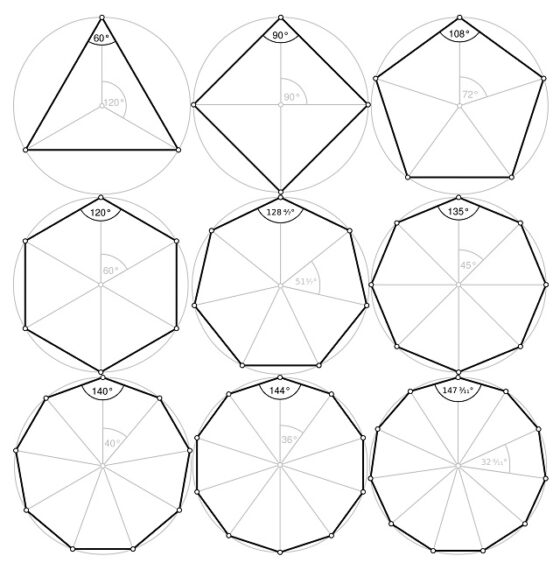
Como se puede observar en la anterior imagen, todos los vértices de un polígono regular convexo se encuentran en una misma circunferencia, la circunferencia circunscrita. Recíprocamente, dada una circunferencia y n puntos regularmente distribuidos en ella, es decir, la distancia entre cada dos puntos consecutivos cualesquiera es siempre la misma, se construye el polígono regular de n lados, uniendo los puntos consecutivos mediante un segmento recto (el lado o arista), hasta cerrar el polígono.

Aunque los polígonos regulares convexos son de sobra conocidos, no lo son tanto los polígonos regulares no convexos, también llamados polígonos regulares estrellados. Veamos primero un ejemplo muy conocido de polígono regular estrellado, el pentagrama o estrella pentagonal. Para construir este polígono estrellado se toman 5 puntos distribuidos de forma regular, es decir, que equidisten los puntos consecutivos, sobre una circunferencia, y luego se trazan segmentos que unan los puntos de forma alternada (se unen cada dos vértices de forma continua hasta cerrar el polígono).

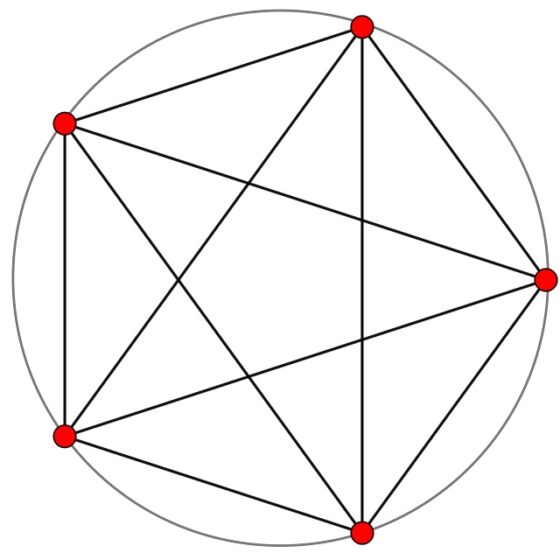
El pentagrama es un polígono regular no convexo, o estrellado, con 5 lados y ángulos (internos) de 36 grados en los vértices. Recordemos que, en el pentágono regular (convexo), el ángulo interno de los vértices es de 108 grados.

Para clasificar los polígonos estrellados se utiliza el símbolo de Schläfli, que para el caso del pentagrama es {5/2}, que nos indica que tiene 5 vértices y están unidos, cada 2 vértices, por segmentos (aristas). En general, el polígono estrellado {p/q} estará formado por p vértices, unidos por segmentos cada q vértices.

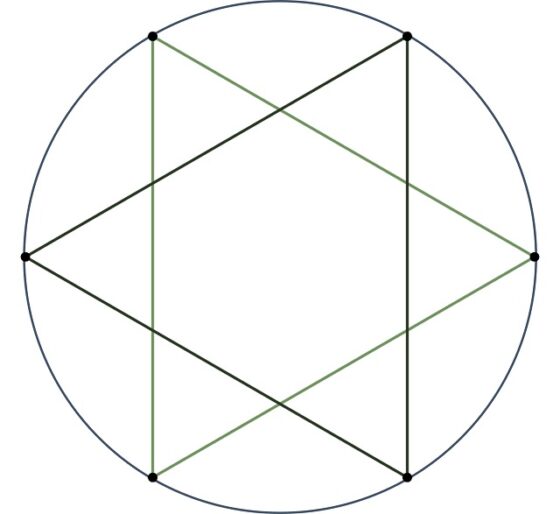
Si queremos construir un polígono regular estrellado con seis aristas, deberíamos considerar seis puntos regularmente espaciados en una circunferencia y podríamos unir los puntos, no de forma consecutiva, ya que obtendríamos el hexágono, que es convexo, sino uniendo cada dos vértices, sería el polígono {6/2}, o cada tres vértices {6/3}. Por desgracia, en ambos casos se obtendrían “polígonos degenerados” (que no son polígonos). En el primer caso, se obtiene el hexagrama que está formado por dos triángulos equiláteros (es, lo que se denomina, un polígono compuesto).

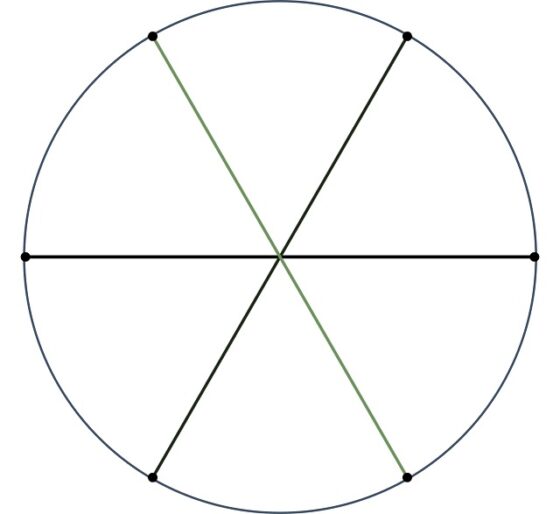
El caso del polígono {6/3} es todavía más degenerado, ya que está formado por tres segmentos rectos que se intersecan en un punto.

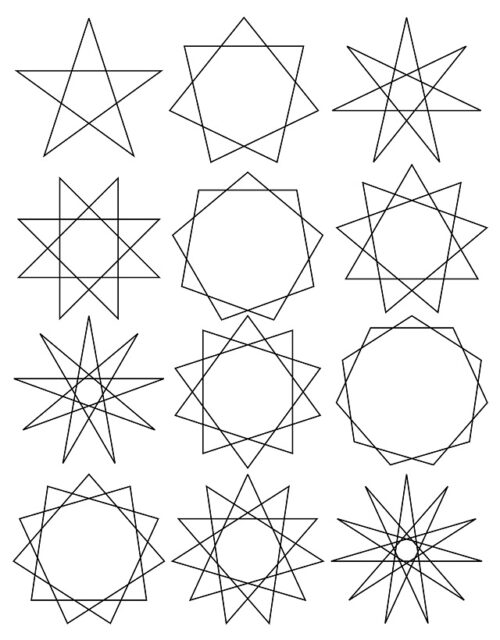
Si lo pensamos un poco, el polígono {p/q} será un polígono regular estrellado (no degenerado) si p y q son coprimos, es decir, que el único divisor común de p y q es el 1. Así, en función de la cantidad de lados tenemos el pentagrama {5/2}, dos heptagramas {7/2} y {7/3}, el octagrama {8/3}, dos eneagramas {9/2} y {9/4}, el decagrama {10/3} y cuatro endecagramas {11/2}, {11/3}, {11/4} y {11/5}, que vemos en la siguiente imagen, y así podríamos seguir aumentando el número de lados.

Para terminar esta sección, planteémonos la siguiente cuestión, si el polígono de la siguiente imagen, que es un decágono (10 vértices y 10 lados), es un polígono regular. La respuesta es negativa, Los lados son todos iguales, pero no sus ángulos interiores, que valen 36 grados y 180 – 36 = 144 grados.

Los poliedros de Kepler-Poinsot

Ahora ya estamos en condiciones de presentar los poliedros regulares no convexos (estrellados), que son los que reciben el nombre de poliedros de Kepler-Poinsot. Existen cuatro de estos poliedros, el gran dodecaedro, el gran icosaedro, el pequeño dodecaedro estrellado, el gran dodecaedro estrellado.

El gran dodecaedro es un poliedro regular que está formado por 12 caras pentagonales (pentágonos regulares), que se intersecan unas con otras, de manera que en cada vértice se encuentran cinco de esos pentágonos (la estructura de cada vértice es la misma), 30 aristas y 12 vértices.

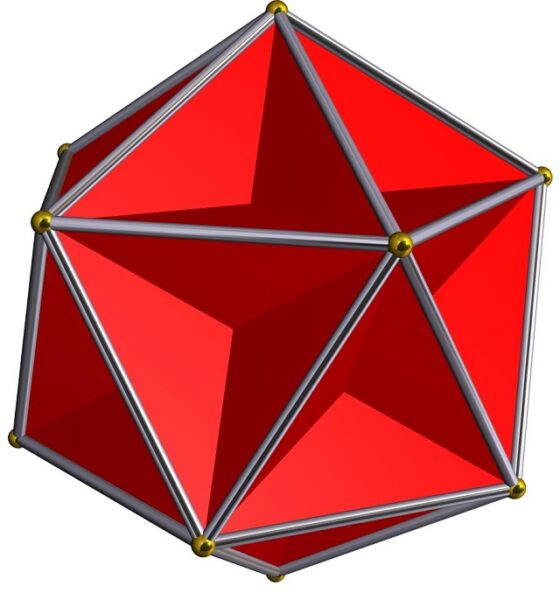
El símbolo de Schläfli del gran dodecaedro es {5, 5/2}. El primer término del símbolo de Schläfli describe las caras del poliedro. En este caso, como el primer término es 5, son pentágonos regulares. Por otra parte, el segundo término indica cual es la estructura (o figura) de los vértices del poliedro. Para el gran dodecaedro, el segundo término es 5/2, luego las caras pentagonales se intersecan como en un pentagrama. Observemos en la anterior imagen que sobre el pentágono que corta a los cinco anteriores, que confluyen en el mismo vértice, se forma, efectivamente, el pentagrama. Por otra parte, los símbolos de Schläfli de los poliedros regulares convexos, los sólidos platónicos, son {3, 3} (tetraedro), {3,4} (octaedro), {3,5} (icosaedro), {4,3} (cubo) y {5, 3} (dodecaedro).

Observemos que, si se consideran solamente las aristas y los vértices del gran dodecaedro, y se toman, como caras, los triángulos equiláteros que unen, de forma natural, las aristas, se obtiene el icosaedro. Es lo que se llama el cierre convexo, que es el conjunto convexo más pequeño que contiene al gran dodecaedro, aunque no hablaremos en esta entrada de este concepto.

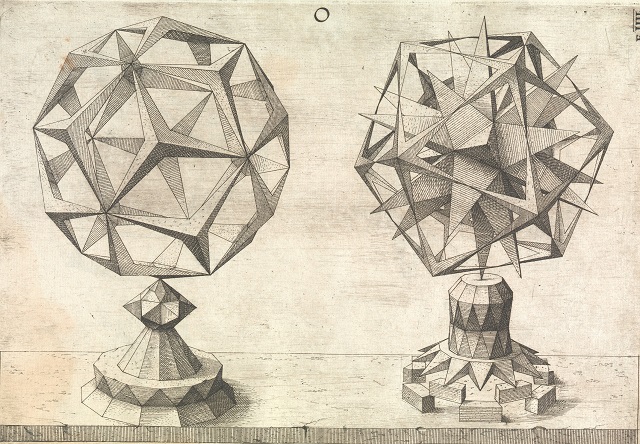
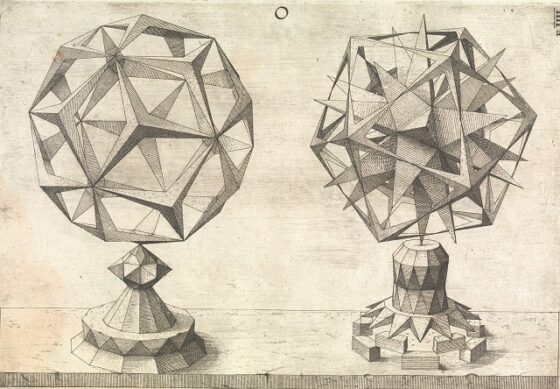
En el libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568) del orfebre y grabador alemán Wenzel Jamnitzer (1507/08-1585), con grabados del grabador suizo-alemán Jost Amman (1539-1591), se muestra un grabado del gran dodecaedro, que es la primera imagen conocida del mismo.

Sin embargo, la primera persona que lo introdujo, desde un punto de vista matemático, fue el matemático y físico francés Louis Poinsot (1777-1859), en su artículo Memoire sur les polygones et sur les polyèdres / Memoria sobre los polígonos y sobre los poliedros (1810). En este artículo Poinsot introdujo los cuatro poliedros regulares estrellados, el gran dodecaedro, el gran icosaedro, el pequeño dodecaedro estrellado y el gran dodecaedro estrellado. Los dos últimos ya habían sido descritos, y estudiados, por el astrónomo, matemático y físico alemán Johannes Kepler (1571-1630) en su libro Harmonices mundi / La armonía del mundo (1619). Por este motivo, se conocen con el nombre de poliedros de Kepler. Mientras que a los dos primeros se les conoce con el nombre de poliedros de Poinsot.

El otro poliedro de Poinsot es el gran icosaedro, cuyo símbolo de Schläfli es {3, 5/2}, ya que sus caras son triángulos equiláteros y la figura de cada vértice está dada, de nuevo, por el pentagrama. El gran icosaedro está formado por 20 caras (triángulos equiláteros), 30 aristas y 12 vértices.

Vayamos ahora por los dos poliedros regulares estrellados de Kepler, que están formados por polígonos estrellados. Empecemos por el pequeño dodecaedro estrellado, que está formado por 12 caras pentagrámicas (pentagramas o estrellas pentagonales), 30 aristas y 12 vértices. Su símbolo de Schläfli es {5/2, 5}, es decir, las caras son estrellas pentagonales {5/2} y en cada vértice se apoyan 5 de esos pentagramas.

La distribución de los vértices en el espacio es la misma que la del icosaedro, por lo tanto, el cierre convexo del pequeño dodecaedro estrellado es el icosaedro.

La primera imagen, de la que se tiene conocimiento, de un pequeño dodecaedro estrellado es un mosaico de mármol, realizado en 1430 por el artista y matemático italiano Paolo Uccello (1397-1475), del suelo de la Catedral de San Marcos, en Venecia (Italia).

En el mencionado libro, Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568) de Wenzel Jamnitzer aparece un pequeño dodecaedro estrellado, al que se le ha cortado parte de las puntas (pirámides) pentagonales, como se puede observar en la imagen.

Y finalmente, el gran dodecaedro estrellado, cuyo símbolo de Schläfli es {5/2, 3}, es decir, las caras son estrellas pentagonales {5/2} y en cada vértice se apoyan 3 de esas caras pentagrámicas. Está formado por 12 caras, 30 aristas y 20 vértices.

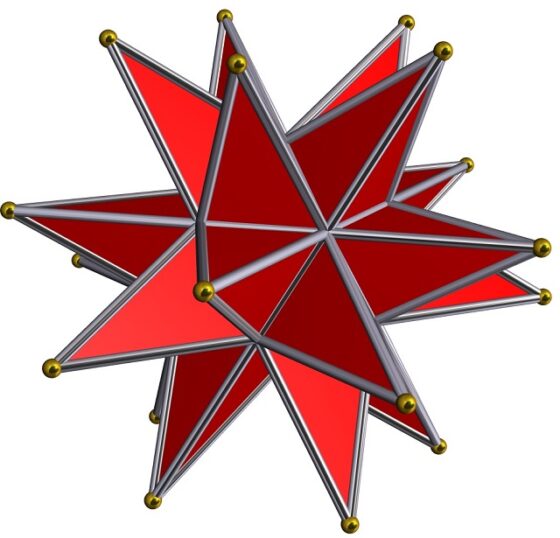
También el gran dodecaedro estrellado está recogido en el libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568) de Wenzel Jamnitzer, como se puede observar en la imagen.

Estos cuatro poliedros regulares estrellados son los únicos que existen, como demostró el matemático francés Augustin-Louis Cauchy (1789-1857).

Bibliografía

1.- Pedro Miguel González Urbaneja, Los sólidos pitagórico-platónicos (Geometría, Arte, Mística y Filosofía), FESPM, 2008.

2.- Claudi Alsina, Las mil caras de la belleza geométrica (los poliedros), El mundo es matemático, RBA, 2010.

3.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.

4.- Alan Holden, Shapes, Space, and Symmetry, Dover, 1991.

5.- Wolfram MathWorld: Kepler-Poinsot Polyhedron

6.- Wikipedia: Kepler-Poinsot Polyhedron

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica