Se han caracterizado las propiedades termodinámicas del modelo de Fermi-Hubbard, que utiliza átomos fríos para simular distintos fenómenos en física de la materia condensada.
Cuando un determinado sistema cuántico resulta difícil de investigar, una opción es estudiar otro que sea físicamente equivalente pero más accesible. Por ejemplo, para comprender cómo se comportan los electrones en un sistema de electrones fuertemente correlacionados (un problema experimental y teóricamente no trivial), los investigadores pueden estudiar una red de átomos fríos (un sistema controlable que obedece las mismas reglas estadísticas que el sistema electrónico más complejo).
Ahora, un equipo de investigadores ha caracterizado exhaustivamente la ecuación de estado para la versión general de un modelo que se emplea para traducir el comportamiento de los átomos fríos en una red al de los electrones correlacionados. Sus resultados confirman la fiabilidad de los tratamientos numéricos de vanguardia de este modelo, lo que lo hace aún más atractivo para estudiar nuevos fenómenos en física de la materia condensada.
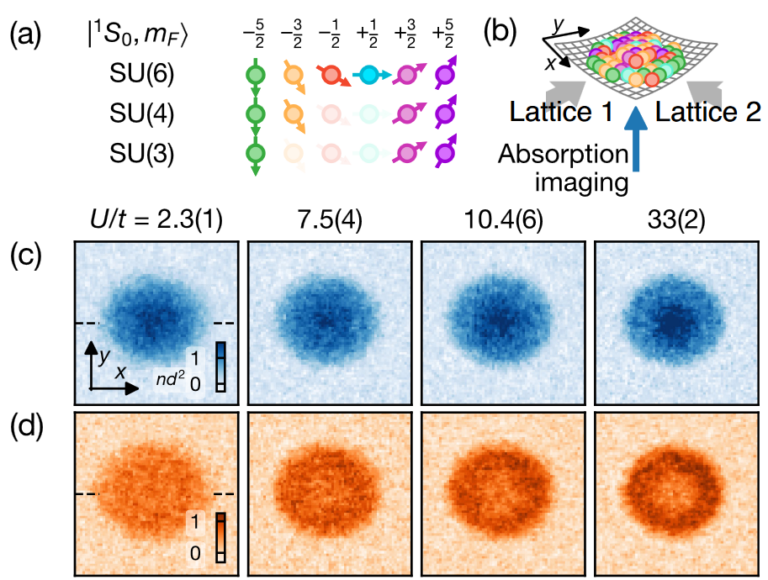
El modelo en cuestión es el de Fermi-Hubbard, que tiene en cuenta las interacciones entre átomos fermiónicos en una red. Los átomos preparados con dos estados posibles se utilizan para explorar problemas que involucran las dos direcciones de espín de un electrón, como el transporte de electrones, mientras que los átomos con más estados se utilizan para explorar fenómenos más complejos, como los nuevos tipos de magnetismo. La ecuación de estado para el modelo de dos estados de Fermi-Hubbard se había caracterizado previamente numérica y experimentalmente. Pero los modelos multiestado, que son más difíciles de manejar numéricamente, siguen siendo mucho menos comprendidos.
Los investigadores utilizaron átomos de iterbio-173, que pueden adoptar seis estados posibles. Midieron las propiedades termodinámicas del modelo multiestado de Fermi-Hubbard utilizando una red de estos átomos y compararon los resultados con las predicciones utilizando los últimos cálculos numéricos disponibles. Las mediciones también accedieron a regímenes que a día de hoy son numéricamente intratables y proporcionaron los datos para derivar una ecuación de estado general para el modelo de Fermi-Hubbard.
Referencias:
G. Pasqualetti, O. Bettermann, N. Darkwah Oppong, E. Ibarra-García-Padilla, S. Dasgupta, R. T. Scalettar, K. R. A. Hazzard, I. Bloch, and S. Fölling (2024) Equation of State and Thermometry of the 2D SU(N) Fermi-Hubbard Model Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.083401
M. Stephens (2024) A General Equation of State for a Quantum Simulator Physics 17, s27
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance