Una elegante demostración del teorema de Morley
El teorema de las trisectrices de Morley es un interesante y atractivo resultado de la geometría del plano, que ha cautivado a muchas personas, en particular, del ámbito de las matemáticas, a lo largo del siglo XX (no es un teorema antiguo) y del que se han desarrollado una cantidad importante de diferentes demostraciones, geométricas, trigonométricas o algebraicas, algunas bastante técnicas, otras de ideas más sencillas y algunas otras de una gran belleza. La entrada del Cuaderno de Cultura Científica titulada El teorema de Morley está dedicada a explicar el significado de este teorema, a acercarnos su historia y a darnos una idea de una de sus demostraciones geométricas. Por otra parte, en esta entrada vamos a mostrar una de las demostraciones más elegantes y sugerentes del teorema de Morley, la demostración que propuso el matemático británico John H. Conway.
El teorema de las trisectrices de Morley
Empecemos recordado la versión simple del teorema de Morley, que no olvidemos que debe su nombre al matemático británico, que vivió gran parte de su vida en Estados Unidos, Frank Morley (1860-1937).
Teorema de Morley (1899): Los puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera, son los vértices de un triángulo equilátero.
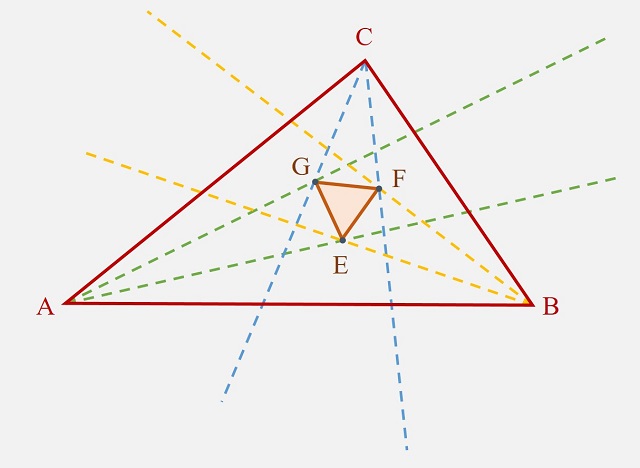
Esto es, dado un triángulo ABC cualquiera, como el de la siguiente imagen, se trazan las trisectrices, es decir, las dos rectas que dividen al ángulo en tres ángulos iguales, de cada uno de los tres ángulos (interiores) del triángulo ABC, se toman los tres puntos que son la intersección de las trisectrices adyacentes, que en la imagen hemos denominado E, F y G, y entonces el teorema de las trisectrices de Morley afirma que el triángulo EFG es un triangulo equilátero (llamado triángulo de Morley), independientemente de la forma del triángulo inicial ABC.
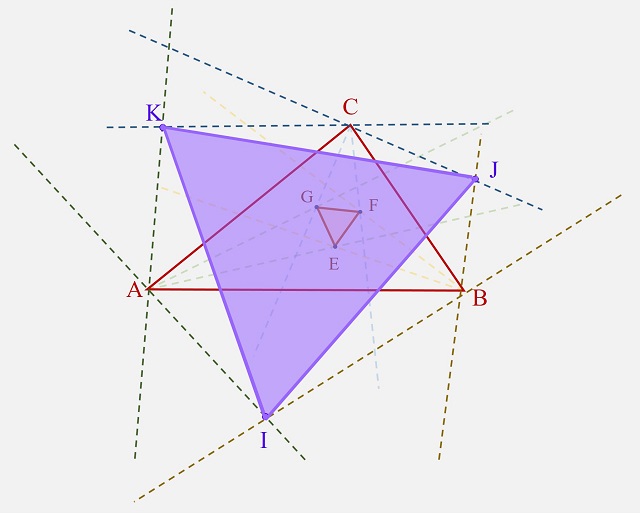
Esta es la versión simple, y más famosa, del teorema, que en su versión completa afirma que existen 18 configuraciones asociadas al triángulo inicial que son también triángulos equiláteros. Por ejemplo, un resultado análogo al anterior se obtiene para las trisectrices de los ángulos exteriores del triángulo.
La demostración de Conway
El matemático británico John Horton Conway (1937-2020), fue un prolífico e imaginativo matemático que trabajó en muchas áreas de las matemáticas, entre ellas la teoría de grupos algebraicos, las matemáticas de los juegos, la teoría de nudos, la teoría de números, la geometría o la teoría de códigos, que escribió interesantes libros, como la trilogía Winning Ways for your Mathematical Plays (Estrategias ganadoras para tus juegos matemáticos), junto a Richard K. Guy y Elwyn Berlekamp, o The Book of Numbers (El libro de los números), con Richard K. Guy, y que es conocido por temas como el autómata celular denominado el juego de la vida, los números surreales o la regla del fin del mundo, entre muchos otros. Os dejo con dos interesantes y profundas opiniones de Conway sobre jugar y educar:
Solía sentirme culpable en Cambridge por pasarme el día jugando a juegos, mientras se suponía que estaba haciendo matemáticas. Luego, cuando descubrí los números surrealistas, me di cuenta de que jugar ES matemáticas.
No se educa a la gente contándole cosas útiles, sino contándoles cosas interesantes.

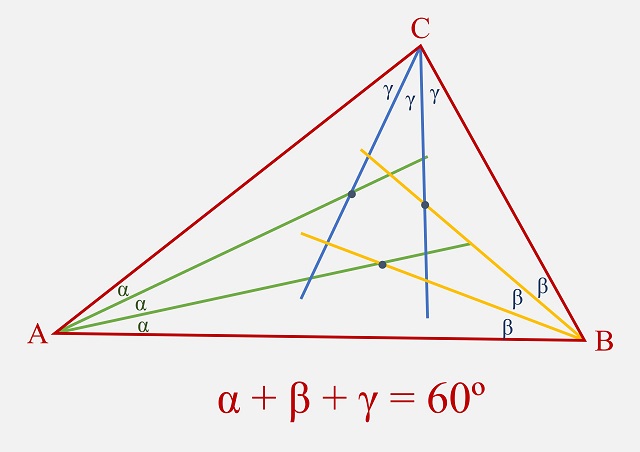
Pero vayamos con la demostración de Conway del teorema de las trisectrices de Morley. Empecemos con un poco de notación. Dado un triángulo ABC cualquiera, como el de la siguiente imagen, del que queremos demostrar que los puntos de intersección de las trisectrices adyacentes de los ángulos (interiores) forman un triángulo equilátero, denotamos por alfa, beta y gama los ángulos que son igual a la tercera parte de los ángulos interiores del triángulo ABC, como aparece en la imagen. Como la suma de los ángulos (interiores) de un triángulo plano suman 180 grados, entonces la suma de alfa, beta y gama es igual a 60 grados.
La demostración de Conway se basa en la creación de un rompecabezas con siete piezas triángulares, una de ellas un triángulo equilátero, de un cierto tamaño, que unidas correctamente forman el triángulo ABC y la pieza del triángulo equilátero es precisamente el triángulo de Morley.
La primera parte de la demostración consiste en la construcción de las siete piezas triángulares. Para empezar, se consideran siete triángulos cuyos ángulos interiores son los siguientes siete triples
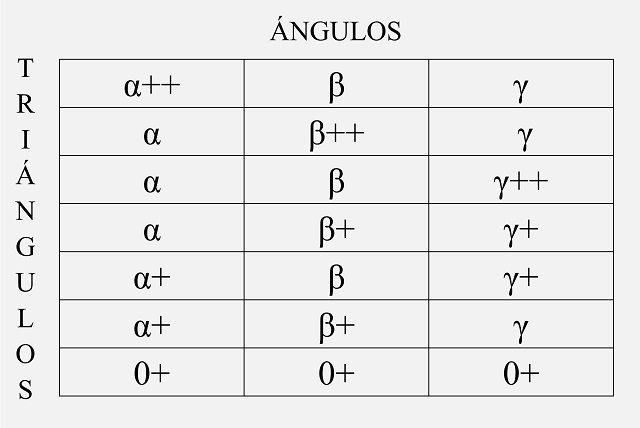
donde el símbolo “+” añadido a un ángulo quiere decir que sumamos 60 grados al ángulo, luego si añadimos dos símbolos “++” querrá decir que se suman 120 grados. Como la suma de alfa, beta y gama es igual a 60 grados, la suma de cada uno de los siete triples de ángulos, de la tabla anterior, es igual a 180 grados, como corresponde a cualquier triángulo. Observemos que uno de los triángulos es equilátero, sus ángulos (interiores) son de 60 grados.
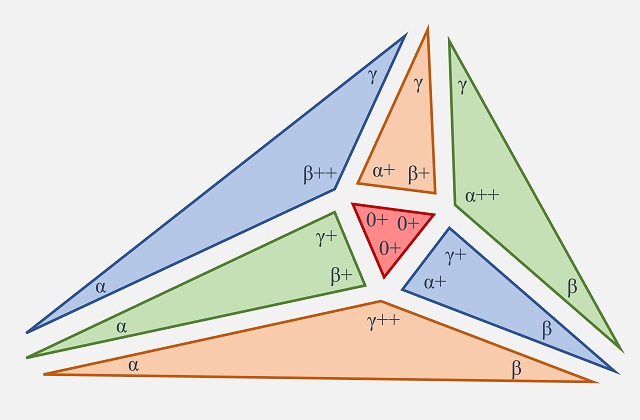
Al determinar los ángulos (interiores) de cada triángulo estamos determinando completamente la forma de dichos triángulos (como se muestra en la anterior imagen), y solo faltaría determinar el tamaño para que puedan encajar convenientemente.
Ahora para decidir el tamaño de las piezas triangulares vamos a proceder de la siguiente manera. Primero fijamos el tamaño del triángulo equilátero, que puede ser de cualquier tamaño, y después iremos adaptando el tamaño del resto de triángulos al de este primero. Para los tres triángulos tales que uno de sus lados se debería apoyar en uno de los lados del triángulo equilátero, que son los tres triángulos agudos (sus tres ángulos son menores de 90 grados), tomamos el tamaño de esos tres triángulos de forma que ese lado sea de la misma longitud que el lado del triángulo equilátero (en la siguiente imagen hemos agrandado y oscurecido esas lados que tienen que tener la misma longitud).
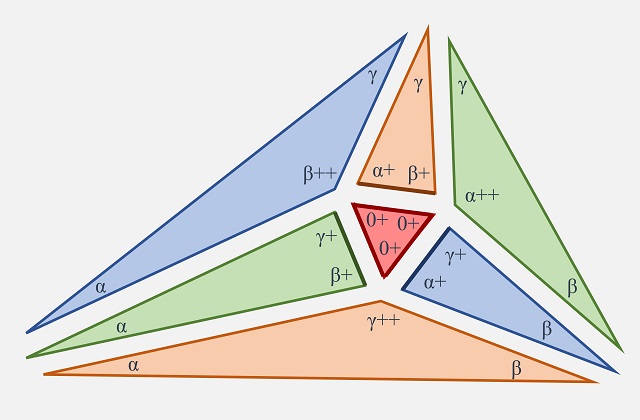
Por otra parte, para determinar el tamaño de los tres triángulos obtusos, es decir, triángulos con un ángulo que mide más de 90 grados, vamos a realizar el procedimiento para el triángulo de la derecha (en el ejemplo que estamos trabajando), el triángulo obtuso verde, procedimiento que se repetirá para los otros dos triángulos obtusos. Se introducen dos segmentos que van del vértice de la izquierda (vértice que se apoyará en uno de los vértices del triángulo equilátero) al lado opuesto, de manera que el ángulo entre estos segmentos y el lado opuesto sea alfa+ (es decir, alfa + 60 grados). Entonces se elige el tamaño del triángulo verde de manera que la longitud de esos dos segmentos (que es la misma, ya que forman un pequeño triángulo isósceles) sea igual al lado del triángulo equilátero.
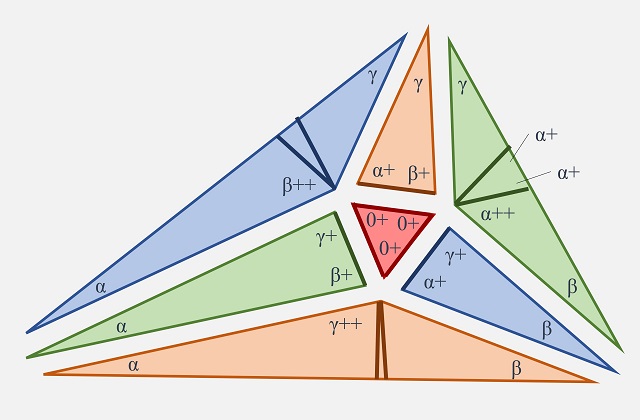
[Observación: Una pequeña aclaración para los más interesados. Si el ángulo en uno de los vértices A, B o C, fuese mayor que un recto, 90 grados, es decir, que uno de los ángulos alfa, beta o gama fuese mayor que 30 grados, entonces al construir ese pequeño triángulo isósceles, el ángulo considerado entre los segmentos y el lado opuesto será el exterior y no el interior]
Por lo tanto, ya tenemos construidos los siete triángulos, con su forma, determinada por los ángulos, y su tamaño, que hemos dispuesto a partir del tamaño del triángulo equilátero central.
El siguiente paso de la demostración consiste en probar que podemos ensamblar bien las siete piezas. Al triángulo equilátero le podemos juntar los tres triángulos agudos, ya que hemos elegido el tamaño de estos para que tengan un lado del mismo tamaño que el lado del triángulo equilátero. Ahora tenemos que comprobar si podemos juntarles además los tres triángulos obtusos, para lo cual tenemos que comprobar que coinciden las longitudes de los lados adyacentes de los triángulos obtusos y agudos. Veamos uno de los lados en cuestión, en concreto, el lado que compartirán el triángulo obtuso verde y el triángulo agudo marrón (arriba a la derecha), los otros cinco se razonan de manera similar.
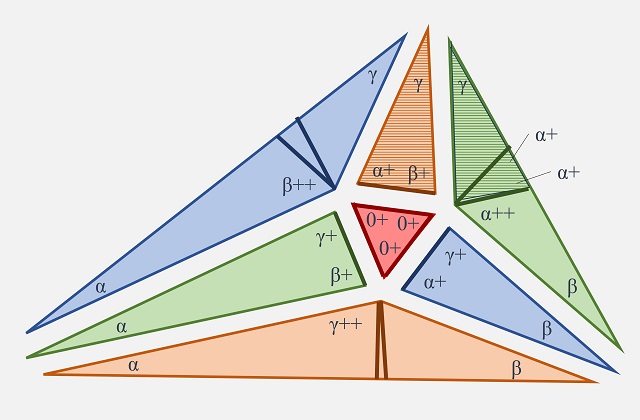
Por la construcción realizada, de ángulos y tamaños, los dos triángulos rayados en la imagen anterior son iguales, sus ángulos son alfa, beta+ y gama+ y tienen un lado de la misma longitud (de hecho, un triángulo rayado es la imagen especular del otro), por lo tanto, los lados adyacentes de ambos son iguales. En consecuencia, el triángulo obtuso verde encaja bien con el triángulo agudo marrón.
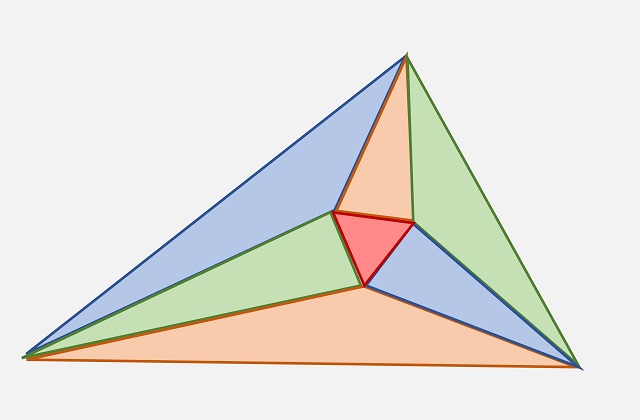
La segunda parte de la demostración queda así concluida al probar que las siete piezas triangulares encajan bien las unas con las otras formando un triángulo más grande entre las siete.
La tercera, y última, parte consiste en comprobar que efectivamente hemos probado el teorema de Morley. Para empezar, el triángulo construido con las siete piezas triángulares tiene ángulos iguales a tres veces alfa, tres veces beta y tres veces gama, como el triángulo ABC, luego ambos tienen la misma forma. Aunque es suficiente, para nuestro propósito, que tengan la misma forma, podemos reescalar el triángulo construido para que coincida, no solo en forma, sino también en tamaño, con nuestro triángulo ABC, basta reescalarlo para que la base tenga la longitud AB.
Por lo tanto, hemos demostrado el teorema de Morley para el triángulo ABC, ya que por la construcción de los triángulos alrededor del triángulo equilátero, los vértices de este son la intersección de las trisectrices adyacentes de los ángulos del triángulo, luego el triángulo que determinan es precisamente nuestra pieza que es un triángulo equilátero. Como decían los matemáticos griegos y seguimos diciendo en la actualidad, QED, es decir, “quod erat demonstrandum” (“lo que se quería demostrar”, literalmente “lo que se iba a mostrar”).

Bibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- Martin Gardner, Nuevos pasatiempos matemáticos, Alianza editorial, 2018.
3.- H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, Mathematical Association of America, 1967.
4.- C. O. Oakley, J. C. Baker, The Morley Trisector Theorem, American Mathematical Monthly 85, pp. 737-745, 1978.
5.- Pedro Alegría, Fernando Blasco, John Conway, el genio mágico, Gaceta de la RSME, vol. 23, n. 3, pp. 463–486, 2020.
6.- John Conway, On Morley’s Trisector Theorem, The Mathematical Intelligencer, vol. 36, n. 3, pp. 3, 2014.
7.- John Conway, The Power of Mathematics, publicado en el libro Power (Alan Blackwell, David MacKay, editores), Cambridge University Press, 2006.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
