En el curioso e interesante libro Lost in translation (Libros del zorro rojo, 2016), de la escritora e ilustradora irlandesa Ella Frances Saunders, descubrí un término muy cercano a mí, bueno, a muchas de las personas que amamos leer. Es el término japonés “tsundoku”, término que se refiere al hábito de comprar libros y dejarlos amontonados sin leer, por ejemplo, en la mesilla al lado de la cama.

En mi mesilla de noche, que es un claro ejemplo de tsundoku, descansan muchos libros comprados esperando a ser leídos. El problema está en que, como compro muchos más libros de los que soy capaz de leer, el tsundoku de mi mesilla crece y crece sin parar, por lo que tengo que quitar libros del mismo para que la torre de libros no sea tan alta que los libros de la misma terminen cayendo al suelo. Por este motivo, algunos de los libros que no son leídos en mucho tiempo acaban siendo trasladados a alguna de mis estanterías de libros y tienen que esperar a que los vuelva a rescatar algún tiempo después para ser colocados en mi mesilla otra vez y leídos finalmente. Aun así, hay muchos libros del tsundoku de mi mesilla que son retirados de la misma por el motivo original por el que fueron colocados allí, porque al final los leo, eso sí, con más o menos distancia temporal del momento en que fueron comprados.

Esto es lo que ha pasado con la magnífica novela Un caballero en Moscú (Salamandra, 2018), del novelista estadounidense Amor Towles (1964), que me recomendó hace un par de años mi librero y tras comprarla pasó a ser incluida en mi tsundoku, hasta hace poco que empecé a leerla. Justo he terminado de leerla el pasado fin de semana y me ha parecido una buena idea escribir un comentario sobre la interesante estructura geométrica de la misma.

Un caballero en Moscú

La novela Un caballero en Moscú (publicada originalmente en Estados Unidos en 2016) es la segunda novela del escritor estadounidense Amor Towles, autor de las novelas Normas de cortesía (Salamandra, 2013) y La autopista Lincoln (Salamandra, 2022), y del libro Mesa para dos (Salamandra, 2024), compuesto por seis relatos y una novela breve.

Un caballero en Moscú se mantuvo durante 59 semanas en las listas de libros más vendidos que publica el periódico estadounidense The New York Times, fue declarada libro del año por los periódicos The Times y The Sunday Times, finalista del Premio Kirkus (otorgado por la revista Kirkus Reviews) en 2016, preseleccionada para el Premio Literario Internacional IMPAC de Dublín de 2018, y se han venido más de un millón y medio de ejemplares de la misma. Además, se ha realizado una serie de televisión británica (Paramount+, 2024), de ocho capítulos, interpretada por el actor británico, nacionalizado estadounidense, Ewan McGregor (1971).

La sinopsis de la novela es la siguiente.

Condenado a muerte por los bolcheviques en 1922, el conde Aleksandr Ilich Rostov elude su trágico final por un inusitado giro del destino. Gracias a un poema subversivo escrito diez años antes, el comité revolucionario conmuta la pena máxima por un arresto domiciliario inaudito: el aristócrata deberá pasar el resto de sus días en el hotel Metropol, microcosmos de la sociedad rusa y conspicuo exponente del lujo y la decadencia que el nuevo régimen se ha propuesto erradicar.

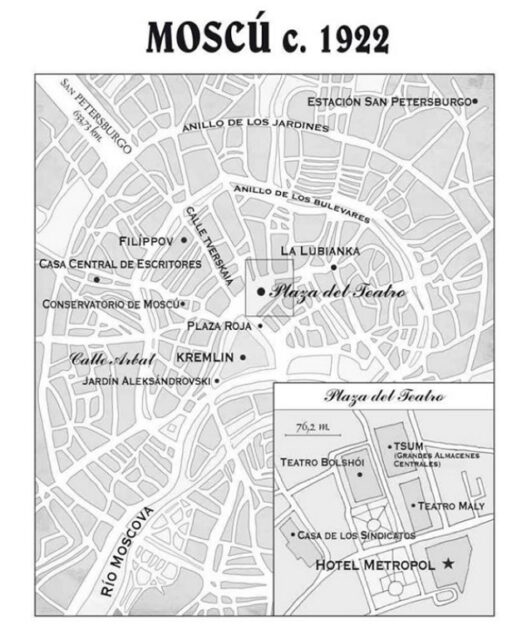
Erudito, refinado y caballeroso, Rostov es un cliente asiduo del legendario Metropol, situado a poca distancia del Kremlin y el Bolshói. Sin profesión conocida pese a estar ya en la treintena, se ha dedicado con auténtica pasión a los placeres de la lectura y de la buena mesa.

Ahora, en esta nueva y forzada tesitura, irá construyendo una apariencia de normalidad a través de los lazos afectivos con algunos de los variopintos personajes del hotel, lo que le permitirá descubrir los jugosos secretos que guardan sus aposentos. Así, a lo largo de más de tres décadas, el conde verá pasar la vida confinado tras los inmensos ventanales del Metropol mientras en el exterior se desarrolla uno de los períodos más turbulentos del país.

Referencias matemáticas en la novela

Aunque el aspecto matemático más interesante de esta novela es su estructura geométrica, de la que hablaremos más adelante, también se incluyen en la misma algunas pequeñas referencias a las matemáticas.

La referencia más larga del libro conectada con las matemáticas trata sobre los números primos y la divisibilidad de los números naturales. La situación es la siguiente. Están juntos el conde Aleksandr Ilich Rostov, protagonista de la novela, y Nina Kulikova, una niña de nueve años muy despierta, inquieta e inteligente, que se hace amiga del conde al principio de la novela, que además le descubre algunos de los secretos ocultos del hotel y ambos mantendrán su amistad a lo largo de los años, hasta que Nina se hace mayor.

– ¿Quieres ver cómo hago un truco?

– Quizá en otro momento.

El conde cuadró la baraja y la dejó encima de la mesa. Entonces, cogió la hoja de encima del montón de hojas terminadas. Vio que en ella estaban concienzudamente alineados en columnas todos los números cardinales del 1100 al 1199. En función de algún sistema que él ignoraba, había trece números encerrado en un círculo rojo.

El conde estaba intrigado, como es lógico.

– ¿Qué estás haciendo?

– Matemáticas.

– Veo que te aplicas a la materia con vigor.

– El profesor Lisitski dice que tienes que pelear con las matemáticas como pelearías con un oso.

– ¿Ah, sí? Y ¿con qué clase de oso peleamos hoy? Sospecho que con alguno más parecido a un oso polar que un panda.

Nina levantó la cabeza y le lanzó una de aquellas miradas suyas capaces de apagar cualquier chispa.

El conde carraspeó y adoptó un tono más serio.

– Me imagino que el proyecto implica ciertos subconjuntos de números enteros.

– ¿Usted sabe qué es un número primo?

– ¿Te refieres a dos, tres, cinco, siete once trece,…?

– Exacto –confirmó ella–. Son los números enteros que son indivisibles por cualquier número excepto el uno y ellos mismos.

Dado el dramatismo con el que había pronunciado la palabra “indivisibles”, parecía que estuviera hablando de la inexpugnabilidad de una fortaleza.

– En cualquier caso –añadió–, estoy haciendo una lista de todos ellos.

– ¡De todos ellos!

– Es una tarea propia de Sísifo –admitió la niña (aunque con un entusiasmo que te hacía preguntarte si conocía realmente el significado de esa expresión).

Nina señaló las páginas escritas que había encima de la mesa.

– La lista de los números primos empieza en dos, tres, cinco, como usted dice. Pero los números primos van haciéndose cada vez más escasos a medida que crecen. De modo que una cosa es encontrar un siete o un once, pero un mil nueve ya es otro cantar. ¿Se imagina identificar un número primo en las centenas de millar? ¿O en los millones? […]

El conde volvió a mirar la hoja que tenía en las manos, esta vez con mayor respeto. Al fin y al cabo, un hombre culto debería admirar cualquier estudio, por misterioso que fuera, si se llevaba a cabo con curiosidad y entrega.

– Mira –dijo con el tono de voz de quien contribuye a una causa–, este número no es primo.

Nina alzó la vista con expresión de incredulidad.

– ¿Qué número?

El conde le puso la hoja delante y señaló la cifra encerrada en un círculo rojo.

– Mil ciento setenta y tres.

– ¿Cómo sabe que no es primo?

– Si la suma de los dígitos que componen una cifra da un número divisible por tres, esa cifra también es divisible por tres.

Ante ese hecho tan extraordinario, Nina replicó:

– Mon Dieu!

Entonces se recostó en el respaldo de la silla y se quedó observando al conde como si reconociera que hasta ese momento quizá lo hubiera infravalorado.

Los números primos son muy importantes en matemáticas y de ellos hemos escrito bastante en el Cuaderno de Cultura Científica (una referencia básica sobre los mismos es la entrada Buscando lagunas de números no primos). En la anterior cita, Nina se encuentra haciendo unos deberes que consisten en realizar una lista de números naturales, en la que se marcan con un círculo rojo aquellos que son primos. Cuando llega el conde ve las hojas en las que Nina está escribiendo esa lista, de hecho, los números de la última hoja realizada contiene los números entre 1100 y 1199. Entre esos números hay doce números primos, que son 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187 y 1193, sin embargo, Nina ha incluido uno más 1173, que no es un número primo, puesto que es divisible por tres, como le descubre el conde, ya que satisface la condición de divisibilidad del tres (“un número es divisible por 3 si, y sólo si, la suma de sus dígitos es divisible por 3”, como mostramos en la entrada Las curiosas reglas de divisibilidad).

Pero existen algunas otras pequeñas referencias matemáticas, como los experimentos del cálculo de la aceleración de la gravedad y el de la torre de Pisa realizado por el matemático y astrónomo italiano Galileo Galilei, la resolución de ecuaciones, la paradoja de Aquiles, el teorema de Pitágoras o la aritmética.

La estructura geométrica de la novela

Pero, sin lugar a dudas, el aspecto matemático más interesante de la novela es su estructura geométrica. La novela transcurre entre el 21 de junio de 1922 y ese mismo día, 21 de junio, día importante en la novela que aparece continuamente a lo largo de la misma, del año 1954, recorriendo 32 años, desde el principio al final. Ese número de años, 32, que es 2⁵ = 2 x 2 x 2 x 2 x 2, no es un número puesto al azar, sino que tiene relevancia en la estructura.

Justo antes de empezar la novela, se presentan las actas del juicio de los bolcheviques al conde Aleksandr Ilich Rostov, celebrado el día 21 de junio de 1922, donde es declarado culpable y se le condena a la pena de muerte. Sin embargo, se le conmuta la pena capital por un arresto domiciliario de por vida en el hotel Metropol del centro de Moscú donde estaba hospedado, debido a que es el autor de un conocido poema subversivo que había escrito diez años antes.

El primer capítulo de la novela (con el título Ante el embajador), tras las actas del juicio, recoge lo que ocurrió ese primer día al llegar al hotel. En particular, se le desaloja de su lujosa suite y se le aloja en una pequeña habitación de una zona en desuso del hotel que estaba destinada a los sirvientes de los huéspedes ricos. El siguiente capítulo (Aquel naufrago anglicano) recoge lo ocurrido un día después del arresto, el 22 de junio de 1922. El tercer capítulo (A la hora acordada) transcurre dos días después del arresto domiciliario. La historia continúa cinco días después (Amistad), luego diez días (Ahora bien…), tres semanas (A dar una vuelta por ahí), seis semanas (Asamblea), tres meses (Arqueologías), seis meses (Adviento) y justo un año después de su arresto en el hotel Metropol, el 21 de junio de 1923 (Abejas en lo alto, una actriz y una aparición).

A partir de ese momento, la novela va saltando a través del 21 de junio de diferentes años, el año 1924 (Anonimato), es decir, han pasado dos años desde la condena del conde, el año 1926 (Adieu), cuatro años después, el 1930 (Artes de Aracne / Acudir a una cita por la tarde / Alianza / Absenta), pasados ocho años, hasta llegar al año 1938, dieciséis años después del primer día de la novela, el 21 de junio de 1922, que es el punto central de la misma (Alguien regresa / Ajustes / Ascenso y descenso).

Como podemos observar los periodos temporales se duplican claramente cuando hablamos del paso de los años (uno, dos, cuatro, ocho, dieciséis años) y se aproxima a la duplicación cuando hablamos de días, semanas y meses (un día, dos días, cinco días, diez días, tres semanas, seis semanas, tres meses, seis meses y doce meses, es decir, un año), que explicaremos más adelante.

A partir de ese punto central, el 21 de junio de 1938, dieciséis años después del inicio de la novela (21 de junio de 1922) y dieciséis años antes del final de la misma (21 de junio de 1954), se produce un reflejo simétrico del paso del tiempo, respecto a la primera mitad, de manera que en esa primera mitad el paso del tiempo se va expandiendo, mientras que en la segunda se va a ir comprimiendo.

Tras el capítulo del 21 de junio de 1938, llega el del año 1946 (Arrebatos, antítesis y un accidente), a ocho años del final, después el año 1950 (Adagio, andante, allegro), a cuatro años del final, el año 1952 (América), a dos años del final y el 21 de junio de 1953 (Apóstoles y apóstatas), a un año del final. Para pasar a seis meses del final (Aplausos y elogios), tres meses (Avanzar como Aquiles), seis semanas (Arrivederci), tres semanas (Adultez), diez días (Anuncio), cinco días (Anécdotas), dos días (Asociación), un día (Antagonistas, frente a frente (y una absolución)) y el final el 21 de junio de 1954 (Apoteosis).

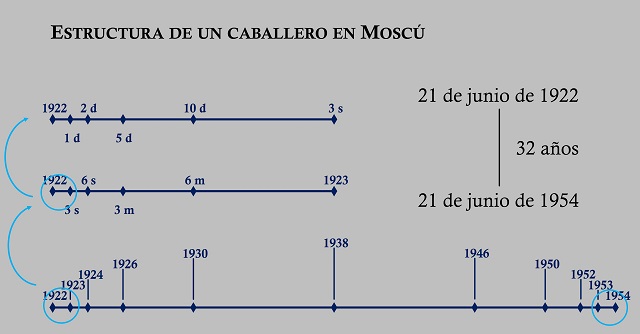
Como hemos comentado más arriba, el paso del tiempo se duplica primero, al menos aparentemente, ya que el paso del tiempo desde el 21 de junio de 1992 hasta el 21 de junio de 1938 es

… un día, dos días, cinco días, diez días, tres semanas, seis semanas, tres meses, seis meses y doce meses, es decir, un año, dos años, cuatro años, ocho años y dieciséis años.

Da la impresión de que algo no está bien, ya que, por ejemplo, el doble de dos días no son cinco días o el doble de diez días no es tres semanas. Veamos que la construcción del tiempo es más bien doblando el tiempo por la mitad, dividir entre 2 y no multiplicar.

El tiempo total de la novela son 32 años (del 21 de junio de 1922 al mismo día de 1954), cuya mitad son 16 años, mitad marcada por el 21 de junio de 1938. La mitad de 16 años son 8 años, que nos lleva al 21 de junio de 1930 (y de forma análoga en el otro sentido, hacia delante, a 1946). La mitad de 8 años son 4 años (1926); la mitad 2 años (1924); la mitad 1 año (1923); la mitad 6 meses; su mitad 3 meses; cuya mitad serían 6 semanas y algo, que puede redondearse a 6 semanas; la mitad 3 semanas; la mitad de 3 semanas, que son 21 días, son 10 días y medio, que redondeando serían 10 días; la mitad 5 días; la mitad 2 días y medio, que redondeando serían 2 días; cuya mitad es 1 día. Luego la estructura se explica con la división temporal en mitades.

La importancia de la estructura geométrica

Esta estructura temporal de la novela es muy importante puesto que marca el ritmo narrativo de la misma. La novela se va expandiendo geométricamente, duplicando prácticamente el tiempo, desde el punto inicial, el 21 de junio de 1922. Al principio los saltos temporales son más cortos, el ritmo es mayor (desde el primer día pasa un día, dos días, cinco días, diez días, tres semanas, etcétera), es el momento en el que se van presentando los personajes de la novela, así como el lugar principal, el hotel Metropol, después los saltos temporales son más largos, el ritmo se va suavizando (cuatro años, ocho años, dieciséis años), que es necesario para percibir el paso del tiempo y los profundos cambios que se están dando en la sociedad rusa, en el propio hotel Metropol y en la vida del protagonista, y luego se contrae el tiempo dirigiéndose hacia la resolución de la novela, con un ritmo cada vez mayor por la compresión del tiempo (faltando para el final tres semanas, diez días, cinco días, dos días, un día).

El propio Amor Towles lo explica en algunas de sus entrevistas. Por ejemplo, en la entrevista realizada por Elena Bowes para “26”, cuando esta le pregunta “¿Puede describir la estructura de acordeón que utilizó para esta novela y por qué la eligió?”, el escritor británico responde lo siguiente.

Un caballero en Moscú tiene una estructura un tanto inusual. A partir del día del arresto domiciliario del Conde, los capítulos avanzan por un principio de duplicación que describe los acontecimientos un día después del arresto, dos días después, cinco días, diez días, tres semanas, seis semanas, tres meses, seis meses, un año, dos años, cuatro años, ocho años y dieciséis años después hasta el día de hoy. En este punto medio, se inicia un principio de división a la mitad, con la narración saltando a ocho años después, cuatro años, dos años, hasta diez días, cinco días, dos días, un día.

El aspecto matemático de la forma del libro es prácticamente invisible para los lectores. Dicho esto, creo que se adapta bien a la historia porque los lectores obtienen una descripción muy granular de los primeros días del confinamiento del Conde; luego pueden saltar en el tiempo a través de épocas definidas por la carrera, las relaciones y los cambios en el panorama político; por último, vuelven a la granularidad urgente a medida que la historia se acerca a su conclusión increíblemente emocionante.

Mientras que en su página web responde también a una serie de preguntas y nos encontramos con el siguiente comentario sobre la estructura de la novela.

Al final, un reto mucho mayor surgió de la geometría de la novela. Esencialmente, Un caballero en Moscú adopta la forma de un diamante de lado. Desde el momento en que el Conde atraviesa las puertas giratorias del hotel, la narración comienza a abrirse sin cesar hacia el exterior. A lo largo de las doscientas páginas siguientes se acumulan descripciones detalladas de personas, habitaciones, objetos, recuerdos y acontecimientos menores, muchos de los cuales parecen casi incidentales. Pero entonces, cuando el libro entra en su segunda mitad, la narración empieza a estrecharse y convergen todos los elementos dispares de la primera mitad. Personajes insignificantes, observaciones pasajeras y objetos fortuitos se entremezclan y desempeñan papeles esenciales para llevar la narración a su aguda conclusión.

Bibliografía

1.- Sarah Hart, Érase una vez los números primos, Paidós, 2024.

2.- Página web oficial de Amor Towles

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica