El problema de la toma de secuencias de decisiones que sean globalmente óptimas, a menudo en relación con la disponibilidad de una capacidad de previsión, es relevante para la aplicación de técnicas y modelos de Inteligencia Artificial en ámbitos tan diversos cómo la robótica y las finanzas (Sargent and Stachurski 2024).

Aunque las tomas de decisiones se refieran típicamente al presente, la posibilidad de retrasar la toma de una decisión específica, reservándonos el derecho de tomarla (o de no hacerlo) en un momento futuro bien determinado, es en sí una posible acción, cuyo valor cabe entender y cuantificar (Roman 2004). Cabe preguntarnos: ¿En qué sentidos la opcionalidad es un elemento significativo para la toma de decisiones (o, mejor dicho, en la definición de secuencias óptimas de decisiones)? ¿Como medir la opcionalidad? ¿Cómo utilizarla?

Aprendizaje por refuerzo

En ciencias de la computación e inteligencia artificial, el aprendizaje automático por refuerzo es un conjunto de metodologías que tiene por objetivo la formulación de secuencias óptimas de decisiones (“políticas”) frente a un entorno (por ejemplo, un videojuego) cuyas reacciones a acciones definidas (cuyas probabilidades de transición) son en principio desconocidas. Usando estas técnicas, un agente automático inteligente aprende a optimizar una recompensa (Malone 1975) que recibe de un entorno simulado o real a las acciones que decide tomar según su observación (potencialmente lagunosa) del estado pasado y actual, determinista y completo o estocástico e incompleto/probabilista del entorno mismo (Sutton and Barto 2018).

La estructura recursiva permite al agente equilibrar recompensas inmediatas con recompensas futuras descontadas.

La limitación fundamental del enfoque de aprendizaje por refuerzo en aplicaciones reales, y especialmente en entornos con espacios de estados y de acciones de alta dimensionalidad y cardinalidad, y potencialmente de limitada observabilidad, se encuentra en su limitada eficiencia en muestreo: llevarlos a la práctica requiere tiempos largos de interacción entre el agente que va aprendiendo y el entorno que observa y sobre en el que acciona, y grandes cantidades de capacidad de cálculo.

Reducir esos costes es valioso, por ejemplo, para poder llevar de forma eficaz herramientas basadas en esas capacidades de gestión óptima a los complejos problemas puestos por las transiciones climático-energética, digital y demográfica.

Esa reducción de costes de entrenamiento puede apoyarse en una extensión de los procedimientos lógicos en base a los cuales se definen los procesos de aprendizaje hacia contextos de incertidumbre como esos entornos desconocidos.

Pero, ¿como juntar probabilidad e incertidumbre, por un lado, y lógica rigurosa por el otro?

La teoría de la probabilidad como lógica extendida

Jaynes (1957) redefine la mecánica estadística, que describe las propiedades y la evolución de sistemas físicos conocidos de forma incompleta, a partir de la propuesta que Shannon (1948) formula para la medición del contenido de la información de un mensaje por ejemplo transmitido por una estación radio. Esa medición se basa en la entropía , un valor (esperado) de la probabilidad del propio mensaje (en bits si el logaritmo es en base 2): mensajes “inevitables”, que ya sabemos que vamos a recibir (“lluvia en Donostia”) conllevan información nula, mientras que mensajes más improbables (“has ganado la lotería”) conllevan información progresivamente más significativa.

Jaynes parece proponer sacar la información/entropía de Shannon del ámbito de la comunicación para darle el rol de una (de la) cantidad física fundamental. La cosecha de esa resemantización: es posible llegar de la entropía a cualquier elemento de la mecánica estadística en pocos elegantes pasos.

Un problema es por un lado, según las observaciones del propio Shannon (1956), la dificultad de verificar empíricamente el carácter “primario” de la entropía/información en las ciencias físicas. Un otro problema (Lairez 2024) es puesto por la necesaria extensión de la interpretación de probabilidad frecuentista clásica bien basada en axiomas (Kolmogorov 1933) en la dirección de una interpretación bayesiana: de la frecuencia de un evento en el limite de infinitas repeticiones de un experimento hacia un “grado de creencia” que es a menudo percibido como inherentemente subjetivo (por ejemplo: quien es el “creyente” respecto a quien se define la medición de probabilidad?) y por consecuencia menos científico.

Por otro lado, si un axioma es un punto de partida completamente arbitrario para un desarrollo formal, cabe observar como los “axiomas” de la teoría de la probabilidad en 1957 ya no son definibles como tales: casi una década antes de Jaynes, Cox (1946) ya se pone el problema de definir una extensión de la lógica binaria de Boole (2003 [1854]) a situaciones y enunciados “grises” con valores de verdad asociados intermedios entre el seguramente falso y el absolutamente cierto a partir de pocos requerimientos básicos (Terenin and Draper 2015).

A partir de esos requerimientos básicos, Cox (1946) consigue llegar a los “axiomas” arriba: cualquier medición consistente (cualquier álgebra) de niveles de certidumbre tiene que seguir las reglas de la teoría de la probabilidad. Los “axiomas” de la teoría de la probabilidad por consecuencia ya no son propiamente axiomas, es decir puntos de apoyo arbitrarios para un desarrollo matemático, sino consecuencias directas de unos requerimientos lógicos. Como propone posteriormente Jaynes (2003): la teoría de la probabilidad, interpretada como una extensión de la lógica, puede representar el marco general para el razonamiento y la inferencia en condiciones de incertidumbre — una base directamente relevante para la Inteligencia Artificial. En esa teoría de la probabilidad reinterpretada como una lógica formal para enunciados inciertos, un rol central es asumido por el teorema de Bayes (Bolstad and Curran 2016), que describe las reglas para actualizar, potencialmente de forma recursiva, unos grados de creencia frente a nuevas observaciones, o, para decirlo mejor, una (distribución de valores de grados de) creencia/certidumbre/credibilidad de un enunciado en base a nuevas evidencias (por ejemplo datos numéricos) .

En esa cadena de actualizaciones recursivas, un problema abierto es evidentemente como definir el punto cero, es decir el punto de partida de esa cadena de creencias progresivamente actualizadas: la distribución a priori, que describe asunciones (y potencialmente prejuicios) antes de la adquisición de cualquier dato.

Una posible superación del carácter subjetivo de la interpretación bayesiana de la teoría de la probabilidad pasa nuevamente por el mismo Jaynes (1957), y por su definición, inspirada en Jeffreys (1946), de los métodos de máxima entropía, que derivan formas funcionales y parámetros de una distribución de probabilidad a priori a través de una maximización de la entropía. La distribución a priori de máxima entropía se obtiene maximizando la expresión de la información de Shannon sujeta a condicionantes que expresan todo lo que es noto o asumido sobre . Diferentes asunciones y prejuicios pueden legítimamente corresponder a distribuciones de máxima entropía diferentes, pero convergerán rápidamente a la misma distribución a posteriori en consecuencia de la misma cadena de observaciones.

Aprendizaje por refuerzo basado en modelos

El aprendizaje por refuerzo basado en modelos intenta definir la información a priori disponible sobre un nuevo entorno a explorar/explotar, para reducir los costes del aprendizaje por refuerzo mediante procedimientos para esbozar mapas de su espacio de fases y configuraciones antes de la fase de experimentación/entrenamiento.

Hasta antes de empezar a interaccionar con el entorno, simplemente observándolo desde fuera, los agentes que maximicen (valores esperados, descontados) recompensas correspondientes con la información según Shannon están aprendiendo de forma implícita a aproximar la distribución que describe las transiciones del entorno. Cestero (2024), por ejemplo, muestra como recompensas basadas en la información de Shannon resultan ser ideales para las fases tempranas y de meta-aprendizaje, de forma independiente de la estructura y del sentido de las recompensas a utilizar para las fases de explotación. En este sentido, maximizar la información disponible en fases tempranas parece ser una buena estrategia de meta-aprendizaje y de observación del entorno mediante una interacción no orientada a una explotación específica. Por ejemplo: la Figura 1 describe como mejoran las capacidades de exploración de un agente que hayan sido inicializados con la experiencia de otro agente (su versión “estudiante”) cuya recompensa “abstracta” y no orientada a resultados aplicativos era una medición de la información según Shannon.

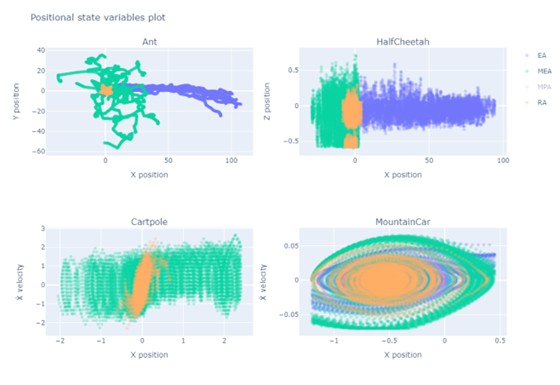
Una manera de hacer concretas estas capacidades adquiridas mediante una interacción no orientada a resultado es, por ejemplo, el algoritmo SMILE (Mutti, Pratissoli, and Restelli 2021), que busca las configuraciones en el espacio de las fases que maximizan una medición de utilidad futura, por ejemplo, para asociarlas a nuevas acciones secundarias, o compuestas o de más alto nivel, en términos de las cuales definir las políticas óptimas a aprender. Se trata, esencialmente, del aprendizaje de un nuevo vocabulario de acciones, máximamente esparzo e informacional, en el que basar la optimización de Bellman. Para ello, son especialmente valiosos mapas del nivel de opcionalidad que conlleva cada posición en el espacio de las fases. Usando el mapa, el agente puede privilegiar esas posiciones.

Lo que resulta de la experimentación con respecto a la búsqueda de nuevas capacidades (skills), y al definir e incluir automáticamente entre las acciones disponibles nuevas secuencias de decisiones que buscan los estados “más interesantes”, es que es exactamente una medición de información de Shannon, que es capaz de identificar configuraciones en las que es difícil entrar y a partir de las cuales es fácil llegar a numerosas nuevas configuraciones (por ejemplo, una puerta difícil de encontrar que en un laberinto dé acceso a una nueva parte del mismo).

El ejemplo en la Figura 2 abajo representa un entorno de juego de agentes de aprendizaje por refuerzo de tipo taxi (Towers et al. 2024), en el que un agente toma el rol de un conductor que recibe recompensas por recoger y llevar a un pasajero a un destino concreto, extendiendo sus características con una gestión energética de una “gasolina” y teniendo en cuenta los costes de movimiento. El problema del entorno es resuelto por ejemplo mediante optimización de política proximal (Schulman et al. 2017), integrado con el aprendizaje a priori y basado en métodos SMILE de nuevas acciones que directamente llevan el taxi hacia localizaciones en el mapa especialmente valiosas en términos informacionales, entrópicos y de opcionalidad.

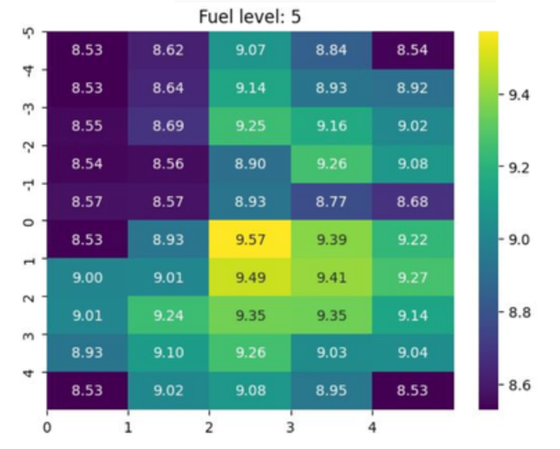
A nivel de resultados, el algoritmo de búsqueda a priori de capacidades y estrategias muestra mejoras claras en la exploración y en la identificación de estados de alta opcionalidad, aunque todavía enfrenta dificultades para aprender de manera eficiente ciertas políticas complejas o altamente especializadas. El resultado de ese análisis a priori del entorno a explorar/explotar es en cualquier caso una significativa mejora en la política óptima identificada por el aprendizaje.

Opcionalidad e información

Los resultados de Cox indican como la entropía de Shannon representa una medición útil para la toma de decisiones del nivel de opcionalidad de un agente en fase de meta-aprendizaje, es decir, con independencia de la recompensa a definir para la fases “prácticas” sucesivas de exploración/explotación. En este sentido, para contestar a las preguntas iniciales, el valor de la opcionalidad, medida en bits, parece ser evidente sobre todo en fases (¿tempranas?) de meta-aprendizaje, en las cuales (¿todavía?) no estén bien definidos los objetivos a perseguir.

Referencias:

Bolstad, William M, and James M Curran (2016) Introduction to Bayesian Statistics. John Wiley & Sons.

Boole, G. (2003 [1854]) An Investigation of the Laws of Thought: On Which Are Founded the Mathematical Theories of Logic and Probabilities. Edited by John Walton and George Maberly. Cambridge University Press.

Cestero, J., Quartulli, M., Restelli, M. (2024) Building Surrogate Models Using Trajectories of Agents Trained by Reinforcement Learning. In: Wand, M., Malinovská, K., Schmidhuber, J., Tetko, I.V. (eds) Artificial Neural Networks and Machine Learning – ICANN 2024 Lecture Notes in Computer Science, vol 15019. Springer, Cham. doi: 10.1007/978-3-031-72341-4_23

Cox, R. T. (1946) Probability, Frequency, and Reasonable Expectation American Journal of Physics 14 (1): 1–13. doi: 10.1119/1.1990764.

Jaynes, E. T. (1957) Information Theory and Statistical Mechanics The Physical Review 106 (4): 620–30. doi: 10.1103/PhysRev.106.620

Jaynes, E. T. (2003) Probability Theory: The Logic of Science. 1st ed. Cambridge University Press. PDF

Jeffreys, H. (1946) An Invariant Form for the Prior Probability in Estimation Problems Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 186 (1007): 453–61 JSTOR: http://www.jstor.org/stable/97883.

Kolmogorov, A. N. (1933) Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer Nature Ergebnisse Der Mathematik 3 (2): 3–47.

Lairez, Didier (2024) Thermostatistics, Information, Subjectivity: Why Is This Association so Disturbing? Mathematics 12 (10). doi: 10.3390/math12101498.

Malone, John C. (1975) William James and BF Skinner: Behaviorism, Reinforcement, and Interest Behaviorism 3 (2): 140–51. JSTOR: https://www.jstor.org/stable/27758839

Mutti, M., L. Pratissoli, and M. Restelli (2021) Task-Agnostic Exploration via Policy Gradient of a Non-Parametric State Entropy Estimate. arXiv arXiv:2007.04640v2 [cs.LG]

Roman, Steven (2004) Introduction to the Mathematics of Finance: From Risk Management to Options Pricing. Springer Science & Business Media.

Sargent, Thomas J, and John Stachurski (2024) Dynamic Programming: Finite States arXiv arXiv:2401.10473v1 [econ.GN]

Schulman, John, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov (2017) Proximal Policy Optimization Algorithms arXiv arXiv:1707.06347v2 [cs.LG]

Shannon, C. E. (1948) A Mathematical Theory of Communication The Bell System Technical Journal 27: 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

Shannon, C. E. (1956) “The Bandwagon (Editorial).” IRE Transactions on Information Theory. Collected Papers Of Claude E. Shannon PDF

Sutton, Richard S., and Andrew G. Barto (2018) Reinforcement Learning: An Introduction. Second Edition. The MIT Press.

Terenin, A., and D. Draper (2015) Cox’s Theorem and the Jaynesian Interpretation of Probability.” arXiv arXiv:1507.06597v3[math.ST]

Towers, Mark, Ariel Kwiatkowski, Jordan Terry, John U. Balis, Gianluca De Cola, Tristan Deleu, Manuel Goulão, et al. (2024) Gymnasium: A Standard Interface for Reinforcement Learning Environments arXiv arXiv:2407.17032v3 [cs.LG]

Sobre el autor: Marco Quartulli es doctor en Electrónica e Informática y responsable del área de Energía y Medio Ambiente de Vicomtech

Sobre Vicomtech: Centro tecnológico espacializado en tecnologías digitales relacionadas con Artificial Intelligence y Visual Computing & Interaction. Transfiere tecnología para que las empresas sean más competitivas y para conseguir un impacto positivo en la sociedad, en coherencia con su compromiso social.

Basque Research & Technology Alliance (BRTA) es una alianza que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.