La hiperesfera, 3-esfera o esfera de dimensión 3, S3, es el análogo en dimensión cuatro de la esfera S2; es decir, la 3-esfera es el conjunto de puntos del espacio real de dimensión 4, R4, que equidistan de un punto fijo, llamado centro.
No es fácil imaginarla, porque no es fácil percibir el espacio de dimensión 4. La fibración de Hopf es precisamente una manera de describir la 3-esfera mediante circunferencias y una esfera.

Si pensamos en la ‘identificación’ entre el espacio real de dimensión 2, R2, y el conjunto de los números complejos, C, una manera alternativa de definir la 3-esfera es la siguiente: la esfera (unidad) de dimensión 3 es el subespacio de C2 (pares de números complejos) formado por aquellos puntos cuya suma de módulos es 1:
![]()
En topología, se usa una descripción alternativa; suele pensarse en la 3-esfera como el resultado de pegar dos toros sólidos (producto de un disco y una circunferencia). En efecto, consideremos los dos toros sólidos de ecuaciones:
![]()
y
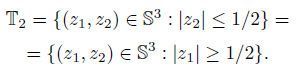
Claramente, se verifica que:
![]()
¿Por qué los anteriores son toros sólidos? Porque la siguiente función es un homeomorfismo (puede probarse lo análogo con T2):
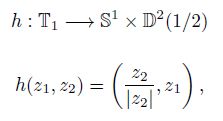
es decir, T1 es (homeomorfo a) el producto de una circunferencia y un disco de radio 1/2 (puntos del plano real que distan del centro menos o igual que 1/2), o lo que es lo mismo, un toro sólido.
Observar que estos dos toros sólidos tienen como frontera común un toro; en efecto:
![]()
que es homeomorfo al producto de dos circunferencias, es decir, un toro.
Esta descripción permite considerar la esfera de dimensión 3 como el espacio de adjunción de dos toros sólidos a través de su frontera común: esta identificación, este pegado, se realiza a través de la aplicación que identifica meridianos con paralelos y paralelos con meridianos:
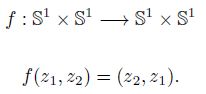
De otra manera, hemos pegado T1 y T2 (homeomorfos a toros sólidos) a través del toro (producto de dos circunferencias)que tienen como frontera común. Por cierto, si la función que identifica los toros frontera hubiera sido la aplicación identidad (que identifica meridianos con meridianos y paralelos con paralelos),
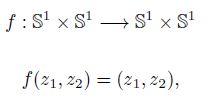
el espacio resultante habría sido el producto de una circunferencia (una 1-esfera) por una 2-esfera, S1xS2,en vez de la 3-esfera.
El matemático Heinz Hopf (1894-1971) descubrió la fibración que lleva su nombre en 1931: encontró, de hecho, una función continua de la 3-esfera en la esfera, en la que cada punto de la 2-esfera proviene de una circunferencia embebida en la 3-esfera. En matemáticas se suele decir que la 3-esfera es un fibrado (no trivial) sobre la 2-esfera, con fibra una circunferencia. Es decir, de manera intuitiva, se puede ver la 3-esfera (la que vive en un espacio real de dimensión 4) como una 2-esfera que en cada uno de sus puntos lleva pegada una 1-esfera.
No es fácil visualizar lo que estamos diciendo, porque estamos trabajando en dimensión 4… pero estos dos videos de la magnífica serie Dimensiones pueden aclarar un poco la anterior construcción:
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
