Las ciudades oscuras es una serie de novelas gráficas, publicadas originalmente en francés, del dibujante belga François Schuiten y el guionista francés Benoît Peeters, cuyo primer álbum Las murallas de Samaris fue publicado en 1983 y que sigue publicándose en la actualidad. En el momento en el que escribo estas líneas cuenta con doce álbumes: Las murallas de Samaris, La fiebre de Urbicande, La Torre, La ruta de Armilia, Brüsel, La chica inclinada, La sombra de un hombre, La Frontera Invisible (doble), La teoría del grano de arena (doble), Recuerdos del eterno presente.

En la colección de novelas gráficas Las ciudades oscuras nos encontramos ante una serie de historias entre fantásticas y surrealistas que transcurren en diferentes ciudades de un continente imaginario que se encuentra situado en el planeta Antichton, o Anti-Tierra. Este hipotético planeta fue inventado por el filósofo y matemático pitagórico Filolao (aprox. 470 – 380 a.n.e.) cuando describió un sistema cosmológico, no geocéntrico, en el que había un fuego central distinto del Sol y un planeta situado en la posición diametralmente opuesta a la Tierra, respecto a dicho fuego central, la anti-Tierra.

La arquitectura y el diseño urbanístico de las ciudades oscuras son protagonistas principales de esta serie de novelas gráficas, pero también la política, la sociedad, la ciencia, las creencias o las relaciones humanas., entre muchos otros

En esta entrada del Cuaderno de Cultura Científica vamos a centrarnos en uno de los álbumes de la serie titulado La fiebre de Urbicande (1985). El protagonista de esta historia es Eugen Robick, el “urbatecto” (unión de urbanista y arquitecto) oficial de la ciudad de Urbicande, que está preocupado por el diseño urbanístico de la ciudad y su falta de simetría. La ciudad de Urbicande está dividida por su río en dos zonas. La zona sur, en la que vive la alta sociedad, sería una ciudad geométrica, con avenidas rectas, que se intersecan perpendicularmente, sobre la que se han diseñado, de forma racional, edificios rectos y simétricos, mientras que la zona norte, en la que vive la parte de la sociedad que la clase alta quiere mantener alejada, posee un desarrollo urbanístico irregular.

Sin embargo, un inesperado acontecimiento cambiará las preocupaciones de Eugen Robick y de los habitantes de la ciudad de Urbicande, la aparición de un misterioso cubo encontrado en unas obras y que se convertirá en el desencadenante de los acontecimientos futuros de la ciudad.

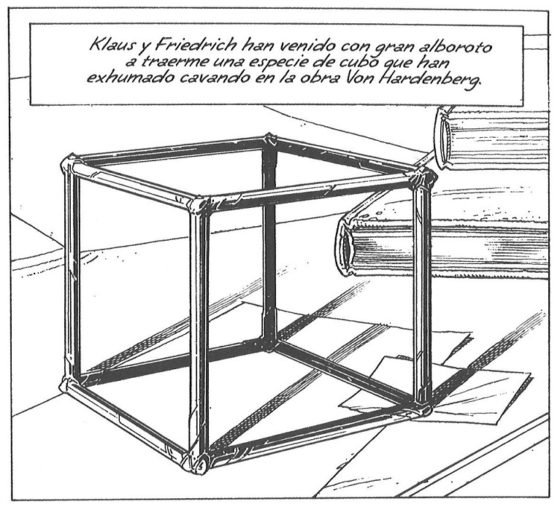
Aparentemente el cubo no posee un gran interés, salvo que está construido con un material extremadamente duro. El urbatecto Eugen Robick lo describe así en las primeras páginas.

“Klaus y Friedrich han venido con gran alboroto a traerme una especie de cubo que han exhumado cavando en la obra Von Hardenberg.

El objeto habría quebrado la pala de una grúa, debido a su gran solidez.

Al observarla fríamente, no tiene sin embargo nada de demasiado extraño. Es una simple estructura cúbica totalmente vacía cuyas aristas no deben de superar los quince centímetros.”

Lo curioso es que, poco tiempo después, del cubo han surgido unas prolongaciones que extendían los lados del mismo, con un crecimiento constante, hasta generar un nuevo cubo en cada una de las caras del hexaedro regular original. De forma que en esta primera etapa se ha creado una pequeña red con 7 cubos. Además, al tiempo que iba ocurriendo esto, el tamaño del cubo original ha ido creciendo también, así en un día el tamaño de las aristas del cubo, de los cubos, ha pasado de 15 a 20 centímetros. El grosor de las aristas también ha ido creciendo paulatinamente.

Como el proceso no para, la red de cubos va creciendo poco a poco, en tamaño y en número de ortoedros que lo conforman. En la siguiente etapa de crecimiento, en cada cara de los cubos que forman la red surgen nuevos cubos, luego de 7 cubos pasa a 25. Y en la siguiente etapa, la red de cubos, que tendrá la forma de un octaedro (es decir, una doble pirámide, hacia arriba y hacia abajo), estará formada por 63 cubos. Después, 129, 231, etcétera.

Eugen Robick, que era matemático de formación según se comenta en la parte de La leyenda de la red, empieza a estudiar la estructura reticular que se genera. En particular, obtiene una fórmula, que veremos más adelante, que le da el número de cubos que tendrá la estructura en cada paso. Pero estudiemos nosotros esa sucesión de números que nos da la cantidad de cubos que posee la red octaédrica que aparece en la novela gráfica.

Empecemos pensando el problema en dimensión 2. Supongamos que nuestra estructura original es un cuadrado, que va creciendo y formando una red de cuadrados de forma similar a como la red de cubos de Urbicande (véase la siguiente imagen). En cada lado del cuadrado original se forma un nuevo cuadrado y sobre los lados de los nuevos cuadrados irán creciendo nuevos cuadrados.

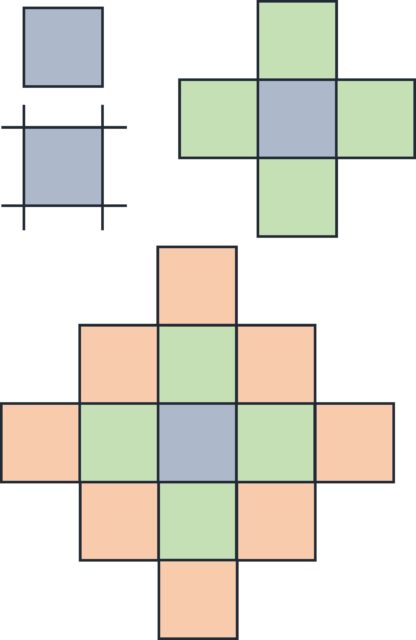
Primero, en el momento cero tenemos 1 cuadrado (c₀), del que surgen 4 más, luego 5 (c₁) en total. En la segunda etapa se incorporan 8, luego 13 (c₂) en total… y así continúa. Pero, veamos cuantos cuadrados se incorporan en cada momento. Si nos fijamos en la anterior imagen, en la segunda etapa (c₂), los cuadrados que se incorporan forman un cuadrado grande (rojo) con 3 cuadrados en cada lado, luego tiene (4 x 3 – 4 = 4 x (3 – 1) = 4 x 2 = 8 cuadrados, es decir, cuatro veces los cuadrados que hay en cada lado menos 4, de los vértices, que contábamos dos veces). En general, en el paso n-ésimo se incorporarán, a los anteriores cubos, 4 x n cubos más. Por lo tanto, se obtiene la siguiente fórmula:

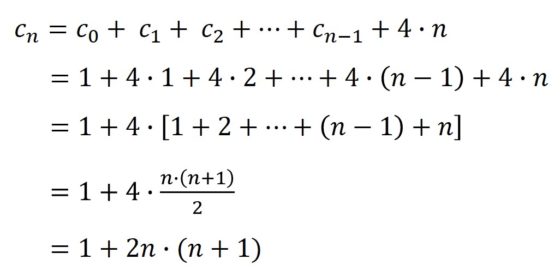
Donde hemos utilizado, en el ante-último paso, la fórmula de la suma de los n primeros números (véase la entrada Matemáticas para ver y tocar ).

El razonamiento que hemos desarrollado en el plano, para cuadrados, no solo nos ayuda a entender el problema en dimensión tres, para cubos, sino que nos permite obtener fácilmente una fórmula para la cantidad de cubos de cada etapa de la red. Esto se debe a que en la etapa n-ésima la cantidad de cubos de la zona/capa central de la red octaédrica es igual a la cantidad de cuadrados de la etapa n-ésima de los cuadrados planos (c_n), ya que solo nos fijamos en los cubos que están a la misma altura, en la misma capa horizontal. En la capa de arriba de la central, y también en la de abajo, hay tantos cubos como cuadrados había en la etapa anterior, luego (n – 1)-ésima de los cuadrados planos (c_{(n – 1)}), y así con el resto. Veamos los primeros pasos. En la primera etapa hay 5 cubos en la zona central y 1 arriba y otro abajo, en total, 7 cubos. En la segunda etapa hay 13 cubos en la zona central, 5 en la zona que está justo encima y 5 en la que está justo debajo, y 1 cubo arriba del todo y 1 abajo del todo, en total 13 + 2 x 5 + 2 x 1 = 25 cubos.

Es decir, tenemos la fórmula general para la cantidad de cubos de la red de Urbicande dada en función de los anteriores números:

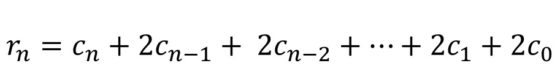
Pero sustituyendo el valor de los números de cuadrados (c_n) calculados anteriormente, se obtiene:

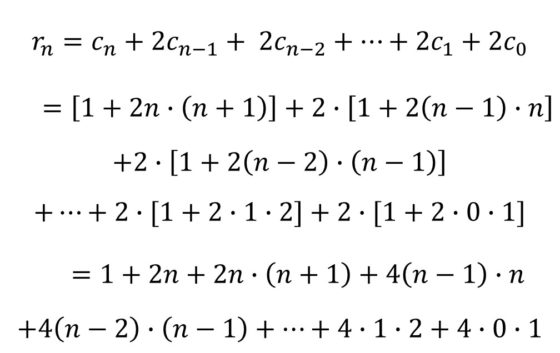
Observemos que en la segunda igualdad hemos sumado primero los 1s de los corchetes, obteniendo el número 1 + 2n del inicio.

Hemos obtenido así una primera fórmula para el cálculo del número de cubos de la red. Si vais dando valores a n = 0, 1, 2, 3, 4, 5, … obtendréis la cantidad de hexaedros regulares de cada etapa 1, 7, 25, 63, 129, 231, …

Vamos a intentar obtener una fórmula más sencilla de manejar. Si denotamos como T_n a los números triangulares, es decir, la suma de los n primeros números, T_n = 1 + 2 + … + n, que sabemos que es igual a n (n + 1) / 2, podemos demostrar que la anterior fórmula es igual a:

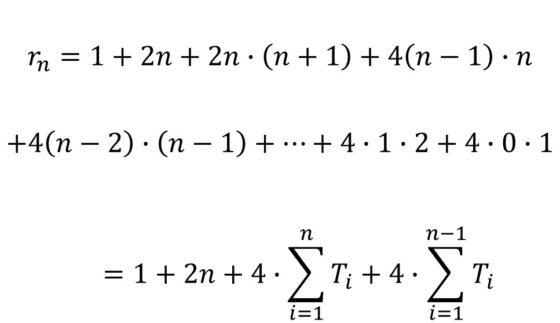
Para seguir avanzando necesitamos la fórmula de la suma de los números triangulares. En la siguiente imagen podéis ver dicha fórmula, con la demostración sin palabras que publicó Monte J. Zerger en Mathematics Magazine (diciembre, 1990) y que aparece también en el libro Demostraciones sin Palabras, de Roger B. Nelsen.

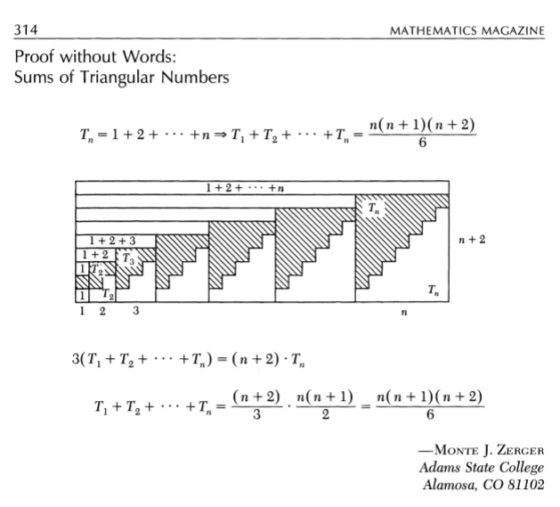
Ahora, haciendo uso de la anterior fórmula se obtiene la siguiente fórmula para la sucesión de cubos que conforman la red octaédrica de La fiebre de Urbicande:

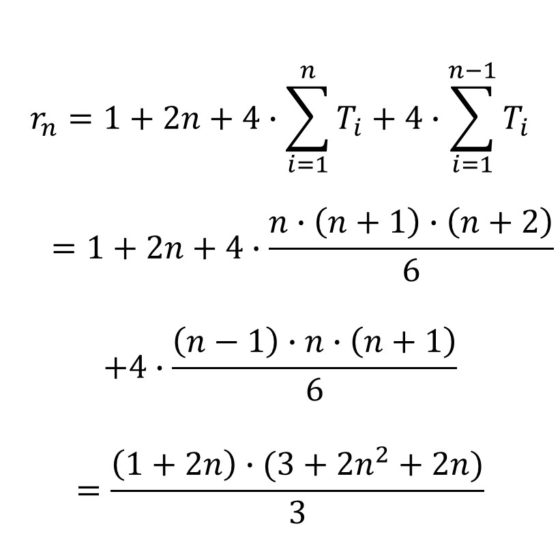
Si volvemos a la novela gráfica de Schuiten-Peeters, podemos observar que la fórmula que he obtenido coincide con una de las dos que aparecen en la misma. Una de ellas es la fórmula de Robick y la otra la que aparece en el opúsculo El misterio de Urbicande “de un tal R. de Brok”, dentro de la parte denominada La leyenda de la red, que es un documento perteneciente a los Archivos de “las ciudades oscuras”.

El razonamiento que utiliza Eugen Robick es diferente al mío y por eso la fórmula que obtiene es diferente. Podemos decir que yo cuento los cubos de cada capa horizontal de la estructura reticular, mientras que Robick cuenta los cubos en columnas verticales.

Expliquemos brevemente la idea de Robick. En la etapa n-ésima del desarrollo de la red la “columna central” de la estructura con forma de octaedro (pirámide doble) tiene 2n + 1 cubos, que es el número que aparece en primer lugar en su fórmula. Después divide la pirámide doble, menos la columna central, en cuatro partes iguales (en la siguiente imagen observamos la partición en lo que sería la vista desde arriba de la red) y calcula la cantidad de cada parte, que es la expresión que aparece multiplicando al 4.

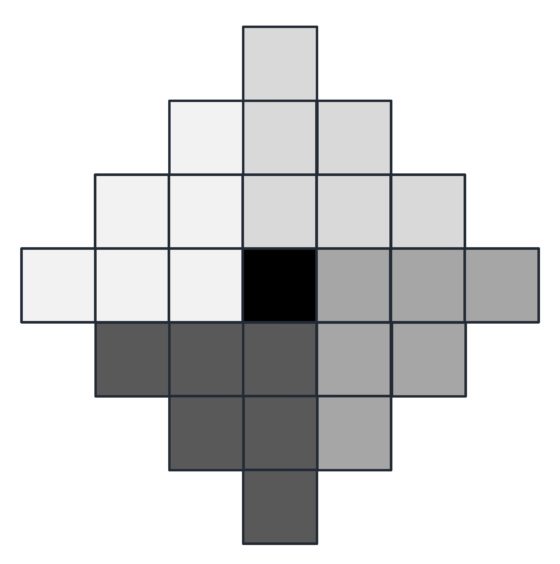
Ahora razonemos visualmente (en la siguiente imagen) cómo obtiene Robick la fórmula del cálculo de los cubos de cada una de esas cuatro partes.

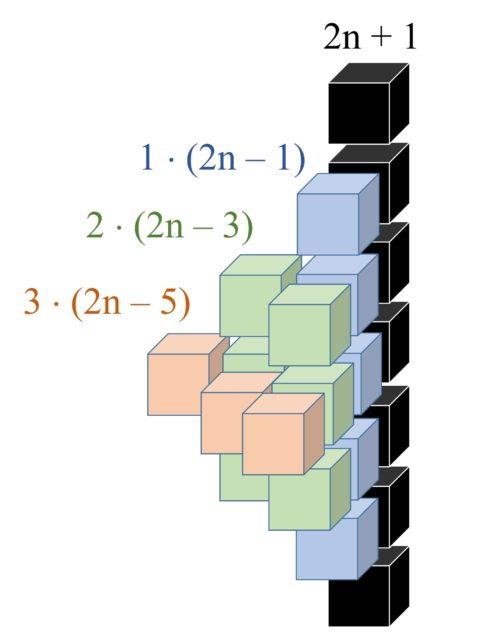
Juntando todo lo anterior se obtiene la fórmula de Robick:

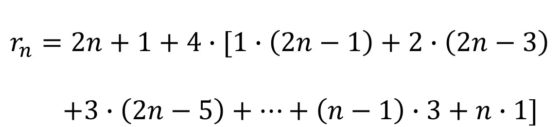
No hemos entrado en el trasfondo social y político de la historia que se cuenta en La fiebre de Urbicande, pero eso dejo que lo descubráis en vuestra propia lectura de la novela gráfica.

Finalizamos la entrada animando a la lectura de la serie de novelas gráficas de François Schuiten y Benoît Peeters, Las ciudades oscuras, y con la imagen de la contraportada de La fiebre de Urbicande de la edición en castellano de Norma editorial en 2015, con tres de los protagonistas de la historia, Eugen, Sofía y el misterioso cubo.

Bibliografía

1.- Francois Schiten, Benoit Peeters, La fiebre de Urbicande (Las ciudades oscuras), Norma Editorial, 2015.

2.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.

3.- Jean-Paul Van Bendegem, A short explanation of «Le Mystère d’Urbicande», Alta plana, the impossible & infinite encyclopedia of the world created by Schuiten & Peeters

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica