El héroe del río es un largometraje cómico (mudo) estrenado en 1928. Está codirigido y protagonizado por Buster Keaton que hace el papel de William, el hijo de Bill Canfield. Canfield es propietario de un barco fluvial que compite con el empresario John James King por el control del transporte de mercancías en el río Mississippi. William y Kitty (la hija de King) están enamorados, provocando el enfado de los padres de ambos.

Casi al final de la película un huracán atraviesa la ciudad. William lucha contra el viento que lo arrastra sin cesar. Tras recibir un golpe en la cabeza, desorientado, permanece en pie, aturdido delante de una casa. La fachada cae sobre él, pero una ventana providencialmente abierta lo salva de morir aplastado (la escena puede verse aproximadamente en el minuto 59:00 de la película). Parece que el actor no permitía que se le doblara en las escenas peligrosas y, en esta, asumió un enorme riesgo. ¿Realizaría algún ensayo antes de filmarla? Desde luego, el protagonista permanece inmutable durante la escena…

Esta secuencia se ha versionado en numerosas ocasiones, desde un episodio de la serie MacGyver hasta alguna película de Jackie Chan, pasando por Deadpan (1997) del cineasta Steve McQueen, en la que él mismo reproduce la escena protagonizada por Keaton casi 70 años antes. Durante casi 20 minutos, desde diferentes ángulos, se puede ver la fachada de una casa que cae sobre McQueen que, al igual que Keaton en 1928, no muestra ninguna reacción.

Consulto cada día la magnífica página Futility Closet que comparte historias sorprendentes sobre temas diversos, entre ellos, la matemática recreativa. En una de sus entradas, Greg Ross introduce un artículo de James Metz publicado en la revista Mathematics Teacher, en el que el autor propone diferentes y sencillos cálculos basados en esta escena de El héroe del río. Es decir, realiza un estudio matemático de la escena, fijándose en algunos de sus fotogramas.

Metz comenta en su artículo que el espacio alrededor de Keaton cuando la ventana “lo atraviesa” es realmente escaso… y tiene razón. Y propone una serie de reflexiones y cálculos para entender con precisión los detalles de la escena. Debajo reproducimos algunas de sus observaciones.

Supongamos que Keaton permanece de pie en el suelo que está situado a 5 pulgadas (1 pulgada = 2,54 centímetros) por debajo de la “bisagra” de la pared que cae. Keaton mide 5 pies y 5 pulgadas (1 pie = 30,48 centímetros; es decir, Keaton mide aproximadamente 165 centímetros). Dejando un margen de 3 pulgadas (7,62 centímetros) por encima de su cabeza, la ventana de altura h debe pasar sobre él a 5,25 pies (1 pie = 12 pulgadas) por encima de la línea de la bisagra. Viendo la escena de El héroe del río, tras la caída completa de la pared, la parte posterior de sus pies está aproximadamente a 0,5 pies (15,24 centímetros) delante de la parte inferior de la ventana. Antes de la caída, la parte inferior de la ventana está a una distancia D de la bisagra de la casa (sobre ella, por supuesto). Resumimos en un diagrama lo anteriormente expuesto:

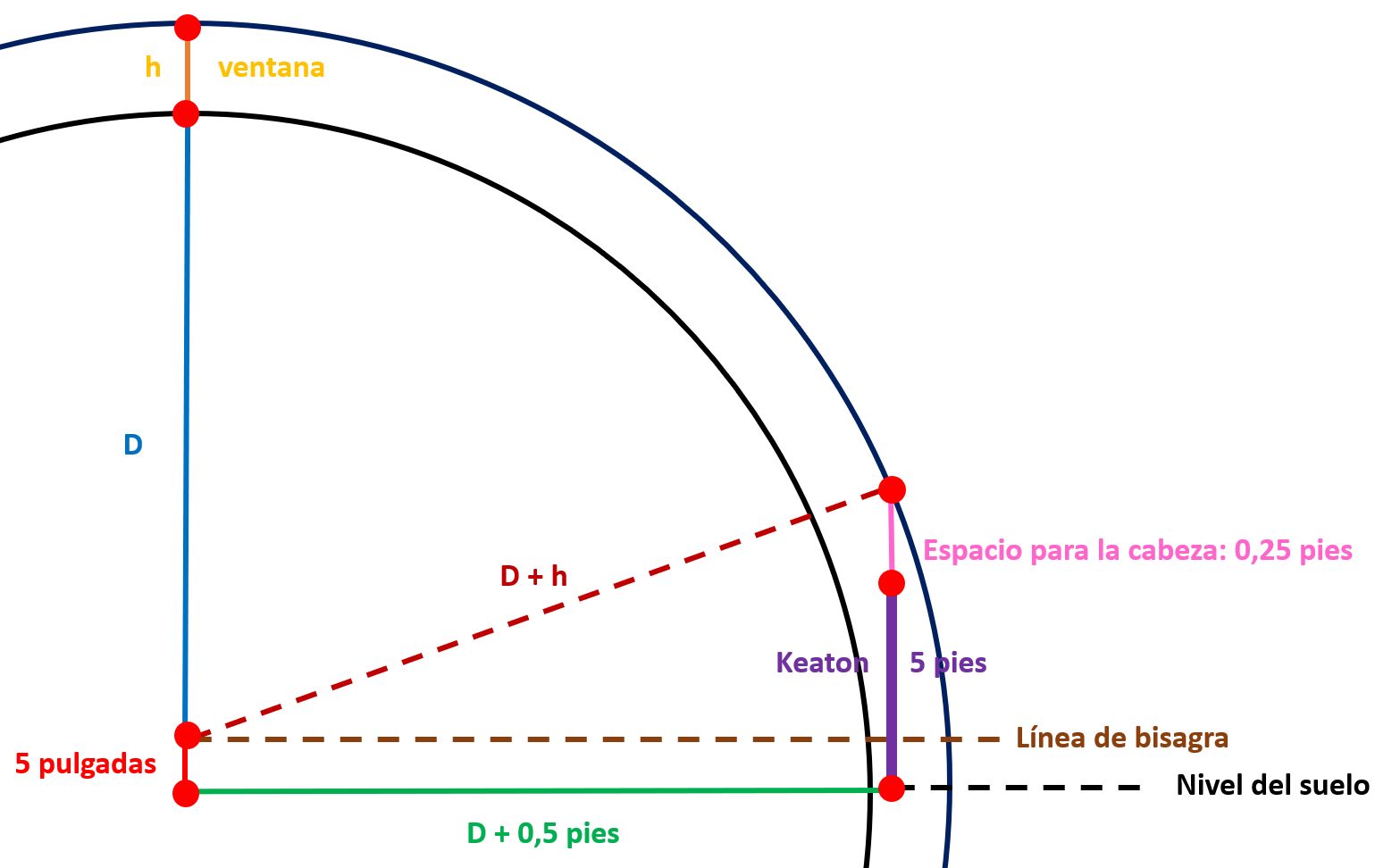
¿Cuál es la relación entre h y D? Se trata de una simple relación entre la hipotenusa y los catetos de un triángulo rectángulo:

(D + h)² = (D + 0,5)² + 5,25².

Si la anchura de los hombros de Keaton es de 1,5 pies (unos 45,72 centímetros) y los lados de la ventana pasan a 3 pulgadas (unos 7,62 centímetros) por cada lado de Keaton, ¿cuál es el ancho de la ventana? Como 3 pulgadas son 0,25 pies, la ventana tiene una anchura de 1,5 + (2 x 0,25) = 2 pies.

Observando de nuevo la escena, supongamos que la relación entre la altura y el ancho de la ventana es de 7/11. ¿Cuál es la altura h de la ventana? Como 7/11 = 2/h, despejando, es h= 22/7, es decir, unos 3 pies (unos 91,45 centímetros).

Ahora podemos calcular D usando la relación entre h y D obtenida antes. Despejando, D = 3,76 pies (unos 114,6 centímetros).

Estos son solo unos pequeños cálculos que nos ayudan a analizar la situación. ¿Serán similares a los realizados por el equipo de Keaton antes de filmar la escena? Como indica Metz en su artículo, se puede generalizar este análisis y hacerse distintas preguntas de tipo «¿qué pasaría si…?».

Referencias:

• Clearence, Futility Closet, 28 agosto 2020
• Steamboat Bill Jr. (1928), película completa, Wikimedia Commons
• James Metz, The Right Place at the Right Time, Mathematics Teacher 112:4 (2019) 247-249

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad