Tres problemas con el 3
Tres árboles caídos
quedaron a la orilla del sendero.
El leñador los olvidó, y conversan,
apretados de amor, como tres ciegos.
Fragmento de “Tres árboles” (1922) de Gabriela Mistral

Hoy, 3 de agosto, proponemos tres problemas con el 3 como protagonista. ¿Sabrías encontrar la solución antes de consultarla?
Tres, eran tres…
En un conjunto Aformado por cinco números enteros positivos, se pide demostrar que siempre es posible elegir tres cuya suma sea un múltiplo de 3.
Solución (ver [1])
La solución pasa por recordar la noción de aritmética modular, en particular, de las congruencias módulo 3. Cualquier número entero n es o bien múltiplo de 3, o bien congruente con 1 módulo 3 (es decir, de la forma n = 3a + 1, donde a es un número entero positivo), o bien congruente con 2 módulo 3 (es decir, de la forma n = 3a + 2, donde a es un número entero positivo).
Supongamos que, en el conjunto A, hay un número de cada tipo, es decir, uno de la forma 3a, otro del tipo 3b + 1 y otro de la forma 3c + 2 (a, b y c son enteros positivos). Entonces, la suma de los tres es: 3a + (3b + 1) + (3c + 2) = 3(a + b + c + 1), que es múltiplo de 3.
En caso contrario, es decir, si las tres posibles congruencias módulo 3 no están representadas en A, entre los cinco números dados, hay necesariamente un tipo de congruencia módulo 3 que se repite al menos tres veces. Tenemos entonces tres posibilidades:
-
Si tres de los números son múltiplos de 3 (3a, 3b y 3c), entonces su suma es 3a + 3b + 3c = 3(a + b + c), que es múltiplo de 3.
-
Si tres de los números son congruentes con 1 módulo 3 (3a + 1, 3b + 1 y 3c + 1), entonces su suma es (3a + 1) + (3b + 1) + (3c + 1) = 3(a + b + c + 1), que es múltiplo de 3.
-
Si tres de los números son congruentes con 2 módulo 3 (3a + 2, 3b + 2 y 3c + 2), entonces su suma es (3a + 2) + (3b + 2) + (3c + 2) = 3(a + b + c + 2), que es múltiplo de 3.
Tres tristes cartas
Tenemos tres cartas cuyos lados son blancos o negros: una de las cartas es blanca/blanca, otra negra/negra y la última blanca/negra. Las introducimos en una bolsa, que agitamos para que las cartas se muevan con facilidad. Sacamos una de las cartas al azar, la colocamos sobre la mesa y observamos que el lado visible es negro. ¿Cuál es la probabilidad de que el otro lado también sea negro?
Solución (ver [2])
Tenemos tres cartas, y por lo tanto seis caras, tres de cada color. De las tres caras de color negro, 2/3 están en la tarjeta negra/negra y 1/3 en la blanca/negra. Por lo tanto, la probabilidad de que el otro lado sea negro es de 2/3.
Un cuadrado tres por tres
En un cuadrado con 3 x 3 casillas pueden colocarse los números del 1 al 9 de manera que en ninguna columna, fila o diagonal aparezcan en orden de magnitud. Se pide demostrar que el dígito que ocupa la casilla central debe de ser impar.
Solución (ver [3])
Llamemos c al número que ocupa la casilla central, que está atravesada por una fila, una columna y dos diagonales.
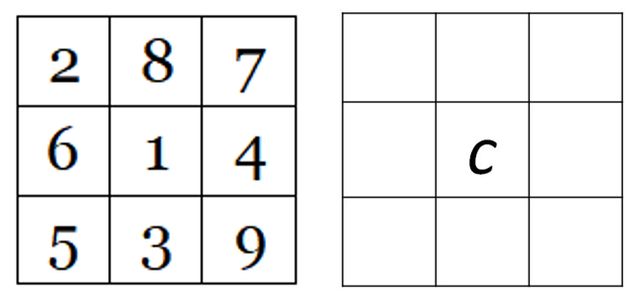
Para cumplir con el requisito impuesto en el enunciado, deben organizarse los ocho dígitos restantes de manera que ninguna de estas cuatro ternas de números (las correspondientes a la fila, la columna y las diagonales que atraviesan la casilla central) esté colocada en orden creciente o decreciente. Es decir, en cada una de estas cuatro ternas, el dígito central c debe ser el número mayor o menor de los tres.
Para conseguirlo, debe completarse cada terna que cruza la casilla central agregando dos dígitos menores o dos mayores (simultáneamente) que c.
Argumentemos ahora por reducción al absurdo. Si el dígito central c fuera par, tendríamos c – 1 números menores que c y 9 – c mayores que c. Al ser c – 1 y 9 – c números impares, se deduce que al menos una de las cuatro ternas que cruzan la diagonal debe completarse tomando un número menor y otro mayor que c, en contra de lo pedido… Así que c es necesariamente impar.
Referencias
[1] Three for Three, Futility Closet, 29 de junio de 2022
[2] The Three Cards Problem, Futility Closet, 27 de febrero de 2008
[3] Odd at Heart, Futility Closet, 20 de diciembre de 2018
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
