En esta entrada del Cuaderno de Cultura Científica vamos a hablar de un interesante juego de estrategia para dos jugadores que fue descrito y estudiado en un libro maravilloso, como es Recreaciones matemáticas (que tenemos la suerte de que esté traducido al castellano, aunque no sea fácil de conseguir en estos momentos), del matemático francés Édouard Lucas (1842-1891) y posteriormente recuperado por el gran divulgador de las matemáticas Martin Gardner (1914-2010), en su columna en la revista Scientific American de juegos matemáticos, en 1963. Se trata del juego militar francés, que recibe también otros nombres como el juego de los soldados, la liebre y los sabuesos, o el halcón y las palomas.

En el volumen 3 de Recreaciones matemáticas (publicado originalmente, de forma póstuma, en 1893), Édouard Lucas habla de un juego con cierta fama en los círculos militares franceses, que recibe el nombre el juego militar, e incluso menciona un evento relacionado con el mismo que ocurrió en un famoso café de París, el café de la Regencia, un sitio habitual de los jugadores y apasionados del ajedrez. Aunque Lucas ya había publicado esa información en el artículo Recreaciones científicas, el juego militar de la revista científica La Nature en el año 1887.

En el citado artículo, así como en el volumen 3 de Recreaciones matemáticas, sobre el juego militar Lucas escribe que el juego aparece mencionado en una revista militar, el Bulletin de la Réunion des officers, de agosto de 1886, otorgándose la autoría del juego a un militar francés, Louis Dyen. Lucas incluye el siguiente párrafo de dicha publicación:

El Sr. Louis Dyen, subteniente retirado, caballero de la Legión de honor, ha dedicado su tiempo libre a la creación de un juego militar que ha ofrecido a la biblioteca y que, por sus variadas combinaciones, da una idea sobre las estratégicas maniobras empleadas por tres brigadas de caballería para cortar las comunicaciones de un cuerpo de ejercito que están asediando. Bajo una apariencia de las más simples, el juego militar presenta una variedad de combinaciones muy complicadas. La partida material del juego se compone de un tablero, parecido al del ajedrez, en el que hay 11 casillas, unidas a sus vecinas por otras tantas líneas rectas, que marcan otras tantas etapas que cada brigada debe superar para cortar al cuerpo de ejército sus comunicaciones y que el cuerpo de ejército dbe superar para evitar ser bloqueado. El cuerpo del ejército saldrá victorioso cuando, tras un número de etapas fijado con anterioridad, no se haya podido inmovilizar; es vencido en caso contrario. Menos difícil que el ajedrez el juego militar es más instructivo y merece ser recomendado como una distracción de las más útiles a los oficiales y a los suboficiales.

Sin embargo, la autoría del juego no está clara. El propio Édouard Lucas escribe la siguiente nota: “Según Martin Gall [que es un seudónimo del campeón de ajedrez francés Jules Arnous de Riviére (1830–1905)], cronista de juegos de combinación del Journal Gil Blas, el inventor del Juego militar sería el Sr. Constant Roy, de Saint-Mandé (Seine) [que son unos suburbios de París]”. El ingeniero francés Constant Roy patentó este juego en enero de 1886 (patente número 173.665) con el nombre Système de jeu dit le stratagème militaire (Sistema de juego llamado la estratagema militar).

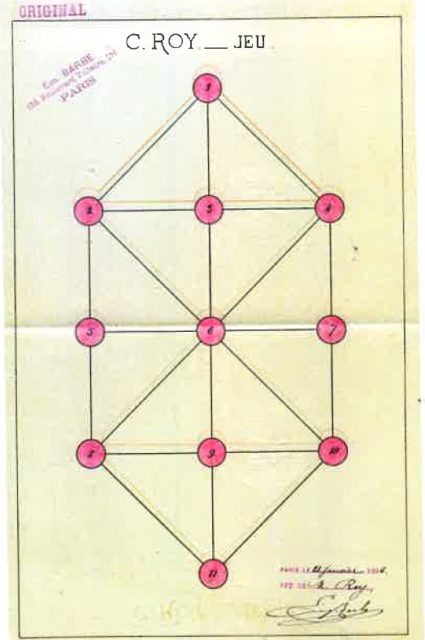
Aprendiendo a jugar

Pero vayamos con las reglas del juego. El tablero consta de 11 casillas, cada una de las cuales está unida por aristas con las casillas adyacentes. Como se puede observar en las imágenes anteriores, las 9 casillas del centro, que forman un cuadrado y están unidas como en el tres en raya (que Lucas numera del 1 al 9, como se ve en la siguiente imagen), mientas que hay 2 casillas más (una la casilla 0 y otra la casilla a, en la siguiente imagen) situadas cerca de dos lados opuestos del cuadrado central y unidas a las tres casillas de cada lado cercano. Y hay cuatro fichas, tres se corresponden con las torres (imagen de Lucas) o las brigadas de caballería (versión de Louis Dyen) en la versión militar o con los sabuesos o palomas (fichas blancas en el siguiente tablero) en las otras versiones, y otra ficha que se corresponde con el cuerpo del ejército, en la versión militar, o con la liebre o el halcón (ficha negra en el siguiente tablero), en las otras versiones.

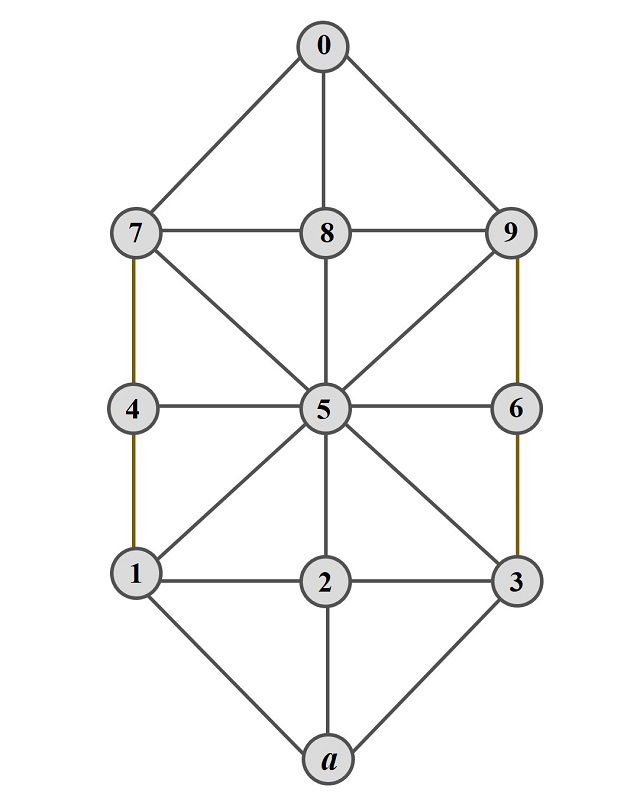
El objetivo del juego es el siguiente, para los sabuesos (fichas blancas) bloquear a la liebre (ficha negra) y para la liebre escapar de los sabuesos.

Las reglas del juego son las siguientes:

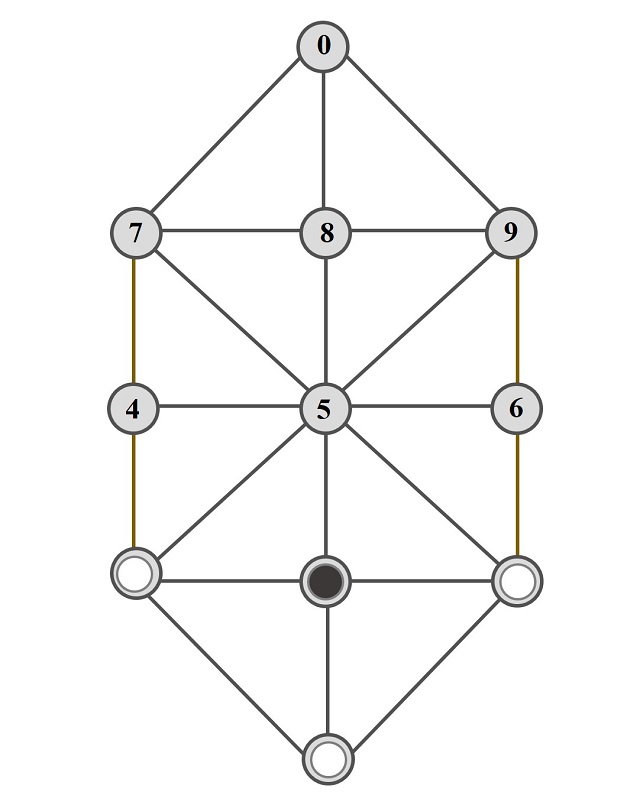
1. En la posición inicial los sabuesos (fichas blancas) están en un extremo del tablero (véase la siguiente imagen), por ejemplo, en las casillas 1, a y 3 de la notación de Lucas, mientras que la liebre (ficha negra) está en la casilla adyacente a las otras tres, la casilla 2 en la notación de Lucas.

2. Hay dos jugadores, uno juega con las fichas blancas (los sabuesos) y el otro con la ficha negra (la liebre), y cada uno de ellos mueve, por turnos, una de sus fichas hacia una casilla adyacente. Y empieza el jugador que juega con la liebre.

3. Las fichas blancas solo se pueden mover lateralmente o hacia adelante, mientras que la ficha negra se mueve en cualquier dirección.

4. Gana el jugador con juega con los sabuesos si estos bloquean a la liebre, es decir, la ficha negra no puede moverse hacia ninguna casilla adyacente, ya que están las fichas blancas bloqueándola; en caso contrario, es decir, si los sabuesos han sido incapaces de bloquear a la liebre, gana el jugador que juega con la liebre.

Pero, como os suelo decir cada vez que hablamos de juegos, lo primero que os recomiendo es

¡Jugar, jugar y jugar!

En el tercer volumen del libro Winning ways for your mathematical plays, de Elwyn R. Berlekamp, John H. Conway y Richard K. Guy, se utiliza un tablero diferente (con casillas que son cuadrados y octógonos, y la adyacencia se da cuando dos casillas comparten un lado), pero que esencialmente es el mismo.

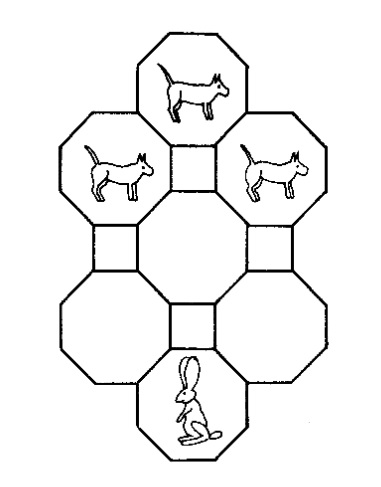
El número de posiciones distintas del juego

Como menciona Édouard Lucas en el prospecto del juego se menciona, entre otras cosas, lo siguiente:

Este nuevo juego, basado en la estrategia militar y que parece, a primera vista, de una gran simplicidad, presenta, al contrario, movimientos difíciles y exige atención continua.

Los jugadores se encuentran pronto en presencia de combinaciones incalculables de defensa y de paso, dependiendo siempre del ataque y de la réplica, lo que permite compararlo con el juego del ajedrez.

A pesar de lo que dice el prospecto de que hay “combinaciones incalculables de defensa y de paso”, más bien el número de posiciones distintas del juego se pueden calcular con facilidad y no es un número excesivamente grande.

El cálculo del número de posiciones distintas del juego es un sencillo cálculo combinatorio. Por una parte, podemos pensar de cuántas formas pueden estar colocadas las fichas blancas (las torres o sabuesos), que son tres, sobre el tablero, que consta de 11 casillas. La respuesta es el número combinatorio C(11, 3), “11 sobre 3”, el número de formas de elegir 3 objetos (en este caso, casillas donde colocar las tres fichas blancas) de entre un total de 11 objetos (las casillas del juego) posibles. Recordemos que el número combinatorio C(n, k) (puede leerse sobre los números combinatorios en cualquier libro de combinatoria, aunque también podéis leer sobre ellos en cualquiera de mis dos últimos libros, La gran familia de los números, cuyo capítulo 6 está dedicado a familias de números que surgen del campo de la combinatoria, o Las matemáticas como herramienta de creación artística, que en su capítulo 4 habla de permutaciones y combinaciones en matemáticas y en arte contemporáneo) es

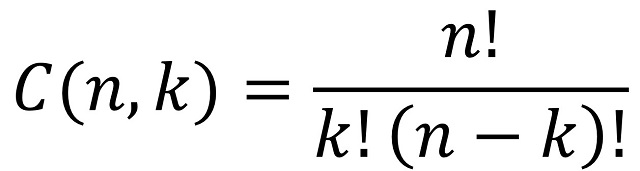
donde la operación factorial está definida como

Por lo tanto, el número de formas en las que pueden estar colocadas las fichas blancas sobre el tablero son C(11, 3) = 165.

Por otra parte, para cada una de esas 165 posiciones distintas de las tres fichas blancas, la ficha negra tiene 8 posibles casillas en las que estar colocadas, luego el número de posiciones distintas del juego, de formas de colocar las tres fichas blancas y la ficha negra son 165 por 8, esto es, 1.320 posiciones distintas del juego.

Aunque puede ocurrir que dos posiciones, aunque sean distintas, sean esencialmente la misma, ya que son simétricas respecto al eje que une las casillas exteriores a y 0, como las dos que se muestran en la siguiente imagen.

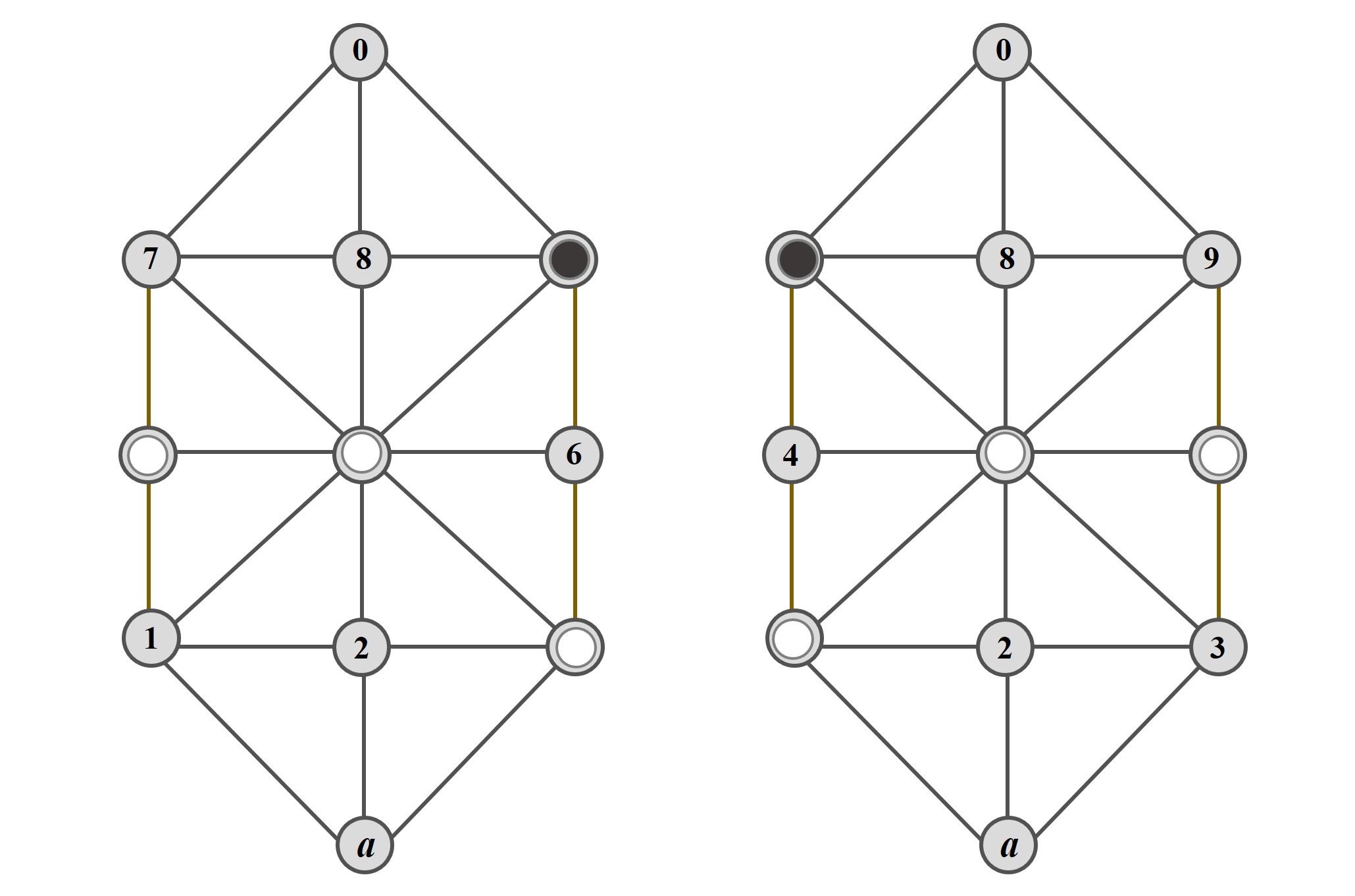
La estrategia ganadora

El prospecto del juego, después de lo anterior, continúa así:

Recompensas de cien francos son ofrecidas por el inventor a las personas que ganen tantas partidas como él mismo, y recompensas de mil francos a las que ganen más de la mitad.

Eso nos hace sospechar que seguramente existe alguna estrategia ganadora para alguno de los dos jugadores, el que juega con los sabuesos o el que juega con la liebre. De hecho, como hemos comentado al inicio de esta entrada del Cuaderno de Cultura Científica el matemático Édouard Lucas ya analizó el juego, mostrando que existe una estrategia ganadora, en concreto, para las fichas blancas.

En primer lugar, Lucas analiza 6 finales de partida (que llama partidas elementales y denomina con las letras A, B, C, D, E y F), donde mueven las fichas blancas, en alguno de los cuales terminará la partida si las blancas juegan según la estrategia que veremos más adelante.

La partida elemental A

En este final de partida, que vemos representado en la siguiente imagen, mueven las fichas blancas y ganan en un solo movimiento. Basta trasladar la ficha blanca de la casilla 5 a la 8 y la ficha negra quedará bloqueada en la casilla 0, sin posibilidad de movimiento.

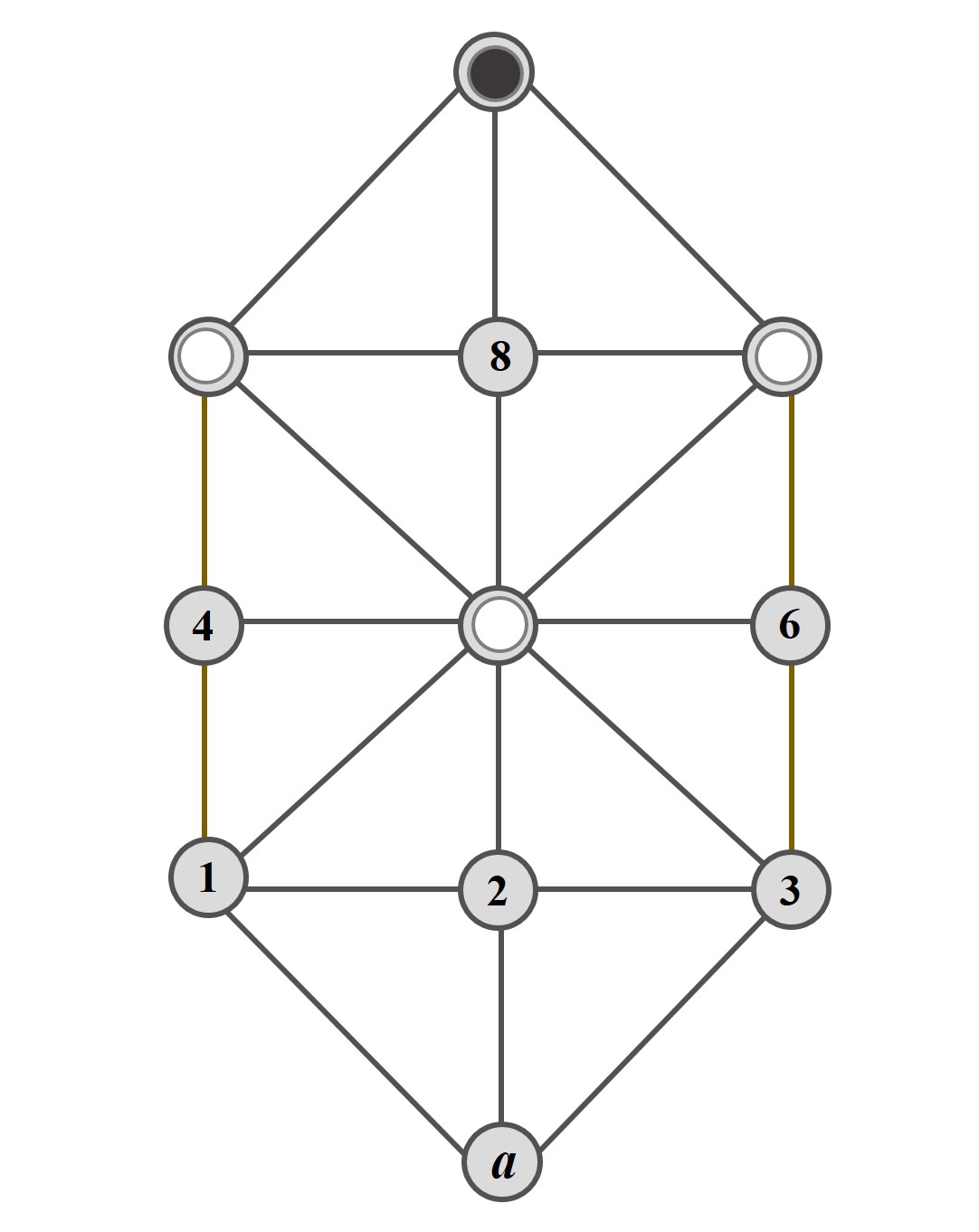
Podríamos describir ese final de partida como 579 0 789, donde los grupos de tres caracteres indican las posiciones de las tres fichas blancas después de que hayan movido las blancas y el grupo de un solo carácter indica la posición de la ficha negra después de que haya movido.

La partida elemental B

De nuevo mueven las fichas blancas y ganan en un solo movimiento, pasando la ficha blanca de la casilla 8 a la 7. Utilizando la anterior notación, la descripción de la partida sería 158 4 157.

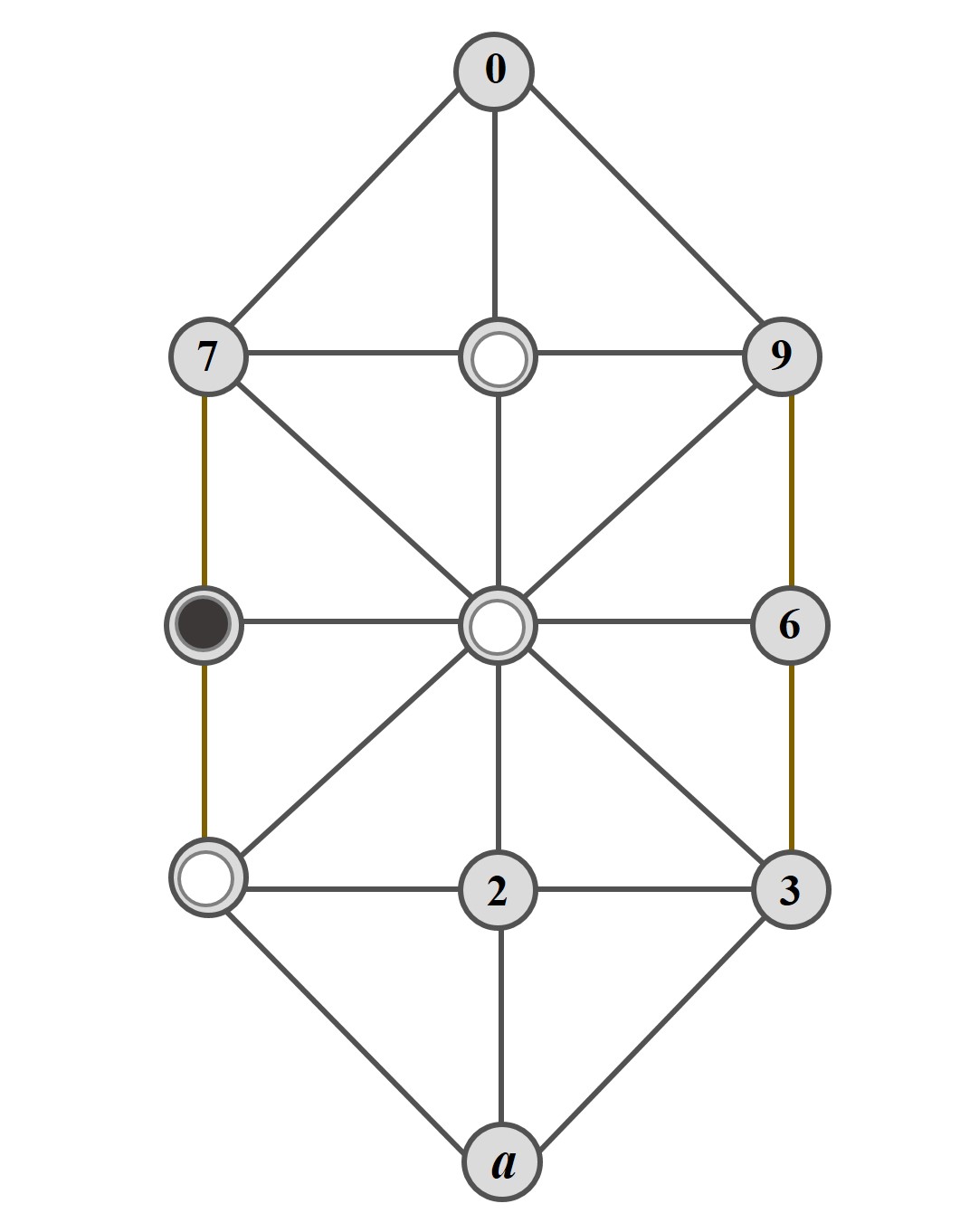
Esta partida nos sirve para explicar que podríamos considerar la partida elemental simétrica (es decir, las fichas blancas estarían en las casillas 3, 5 y 8. mientras que la ficha negra estaría en la casilla 6), cuya solución es idéntica (la ficha de la casilla 8 pasa a la casilla 9). En todo el estudio que hace Lucas, y que estamos explicando aquí, evita repetir el análisis para las posiciones simétricas.

La partida elemental C

Para esta partida elemental donde dos de las fichas blancas están en las casillas 7 y 9, la otra ficha blanca puede estar en cualquiera de las casillas 1, 2, 3, 4 o 6 (que en la siguiente imagen hemos indicado dando un poco de color amarillo a la ficha), mientras que la ficha negra está en la casilla 8.

Las blancas mueven y ganan en dos movimientos. Se mueve la ficha blanca que está en la tercera casilla (una de las casillas 1, 2, 3, 4 o 6) a la casilla del centro, la casilla 5, luego a la casilla negra no le queda más remedio que ir a la casilla 0, y llegamos a la partida elemental A.

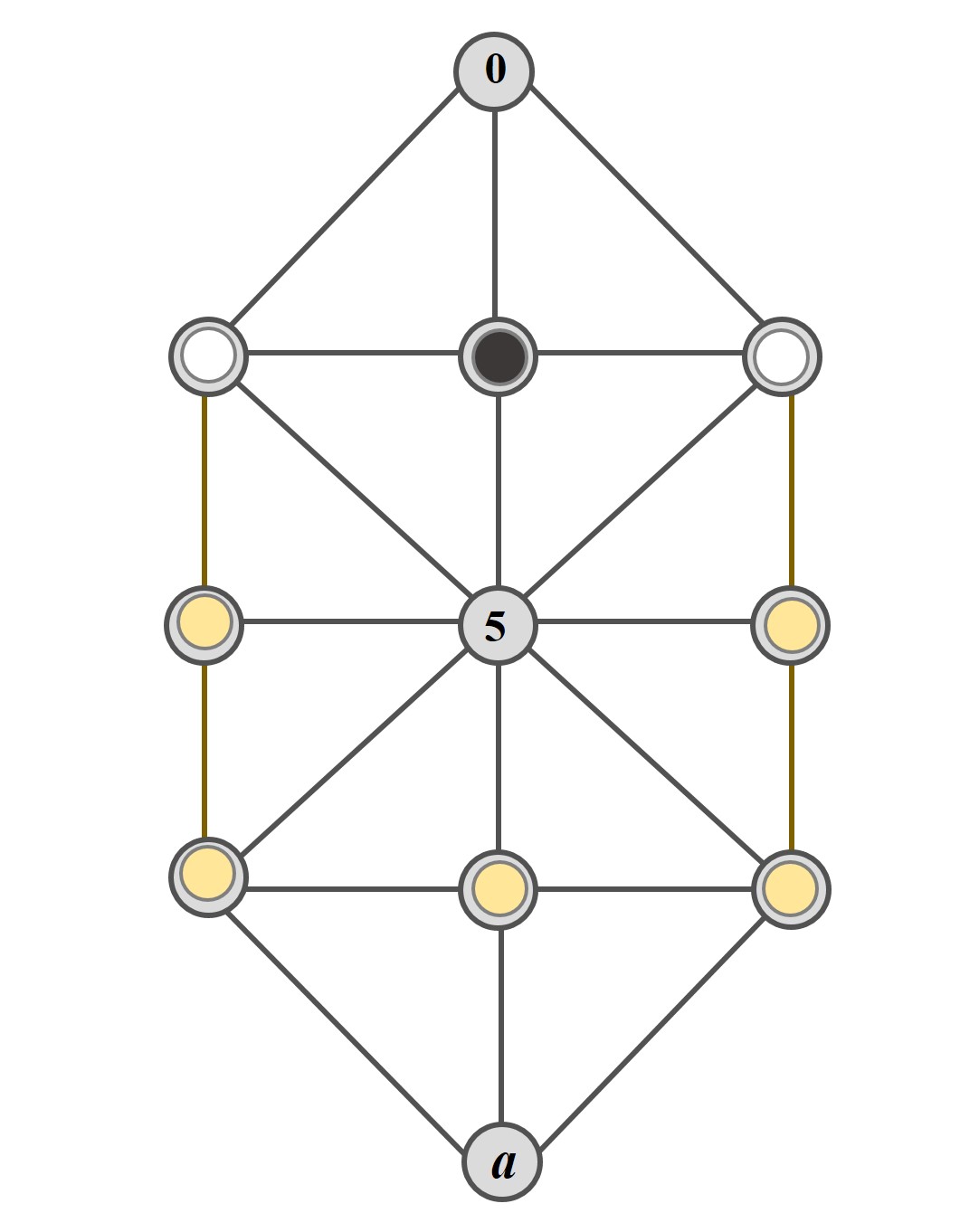
Según la notación de Lucas, asumiendo que la tercera ficha blanca estuviese en la casilla 1 (de forma similar para el resto), la partida elemental C se describiría como 179 8 579 0 789.

La partida elemental D

Otro sencillo final de partida en el que mueven las blancas y ganan en dos movimientos. Basta llevar la ficha de la casilla 6 a la 9, y estaremos en la partida elemental A. La descripción de la misma sería 567 8 579 0 789.

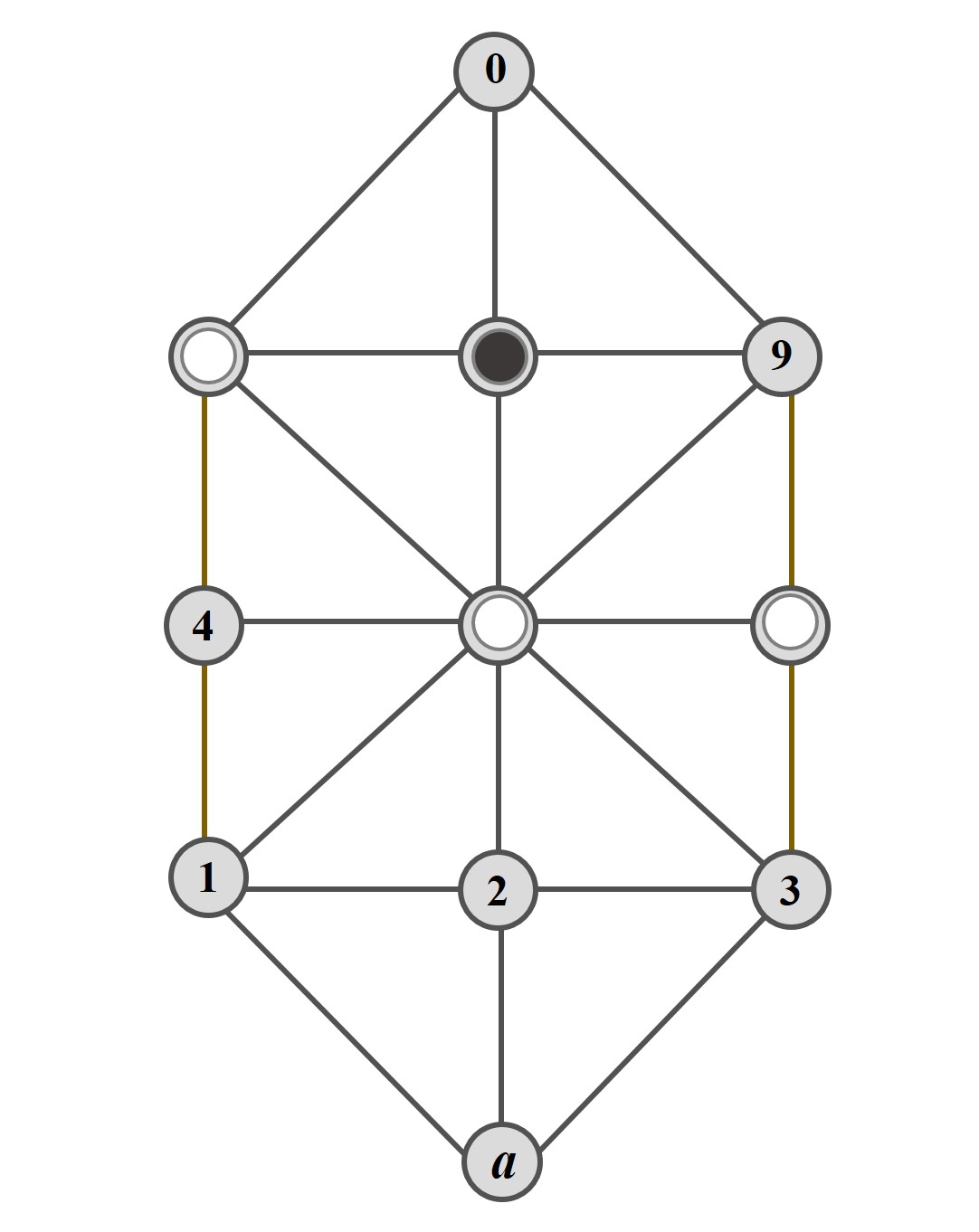
La partida elemental E

Esta partida elemental es, de nuevo, múltiple, como la partida C. Las dos primeras fichas blancas están en las casillas 5 y 7, mientras que la tercera estará en una se las siguientes casillas, 1, 2, 3, 4 o 6, como antes, mientras que la ficha negra estará en la casilla 0. Ahora, las fichas blancas necesitan tres movimientos para ganar. Las fichas blancas mueven de 5 a 9, la ficha negra solo puede mover a 8, quedando la posición de la partida elemental C.

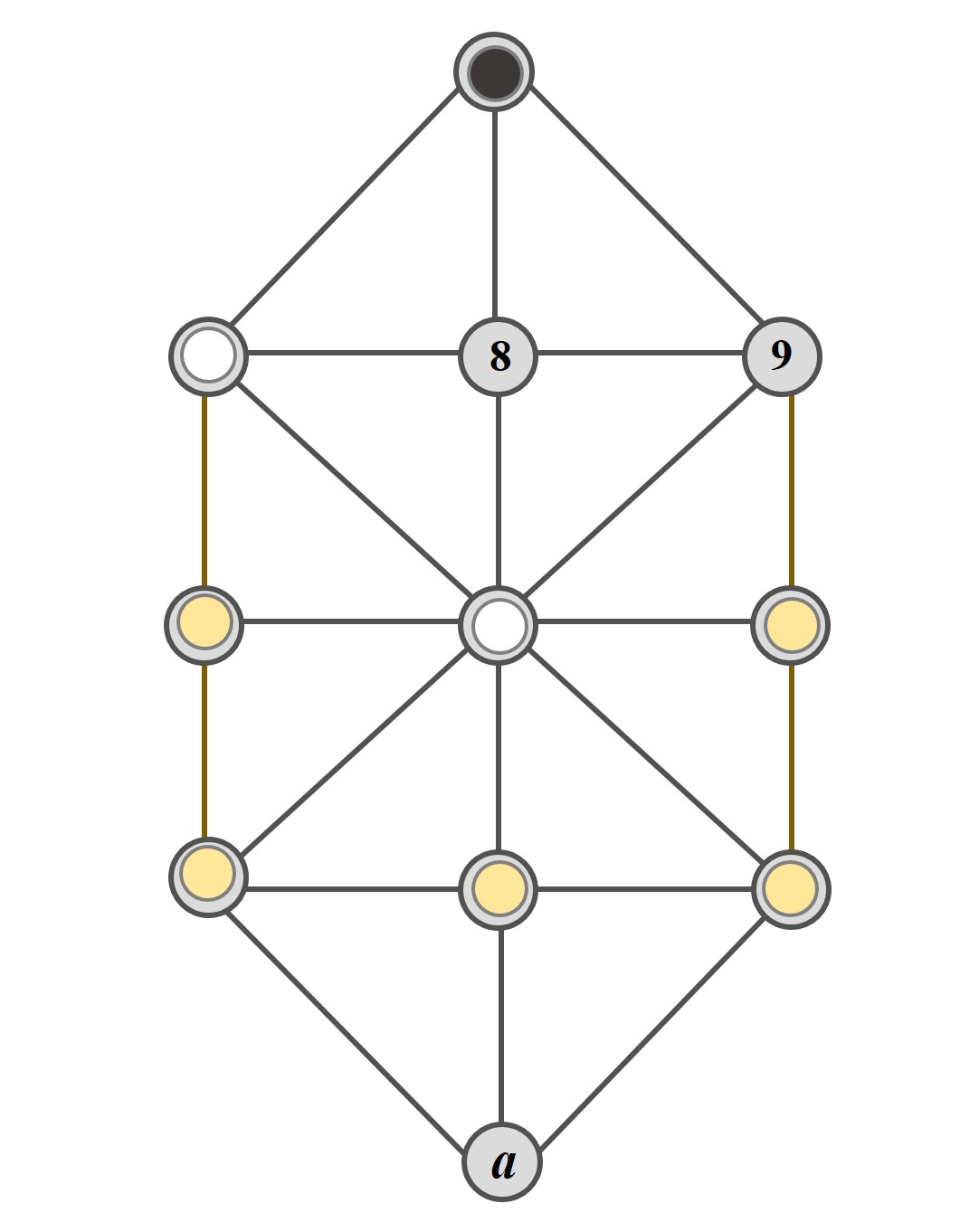
La partida elemental F

En esta posición las fichas blancas mueven y ganan en 3 o 4 movimientos, en función de los movimientos de la negra. Para empezar las blancas mueven de la casilla 1 a la 4, y la ficha negra, que está en la casilla 7, tiene dos opciones, mover a la casilla 8 o a la casilla 0. En función del movimiento de la ficha negra, las blancas moverán en consecuencia. Si la ficha negra pasa a la casilla 8, será la posición simétrica a la partida elemental D, y las blancas ganarán en dos movimientos más (las blancas mueven de 4 a 7, la negra retrocede a 0 y las blancas mueven de 5 a 8, quedando bloqueada la negra), mientras que si la ficha negra pasa a la casilla 0, las blancas mueven de 5 a 7 y la ficha negra de 0 a 8 quedando la posición elemental C y las blancas ganan en dos movimientos (las blancas mueven de 4 a 5, las negras retroceden a la casilla 0 y las blancas la bloquean moviendo de 5 a 8).

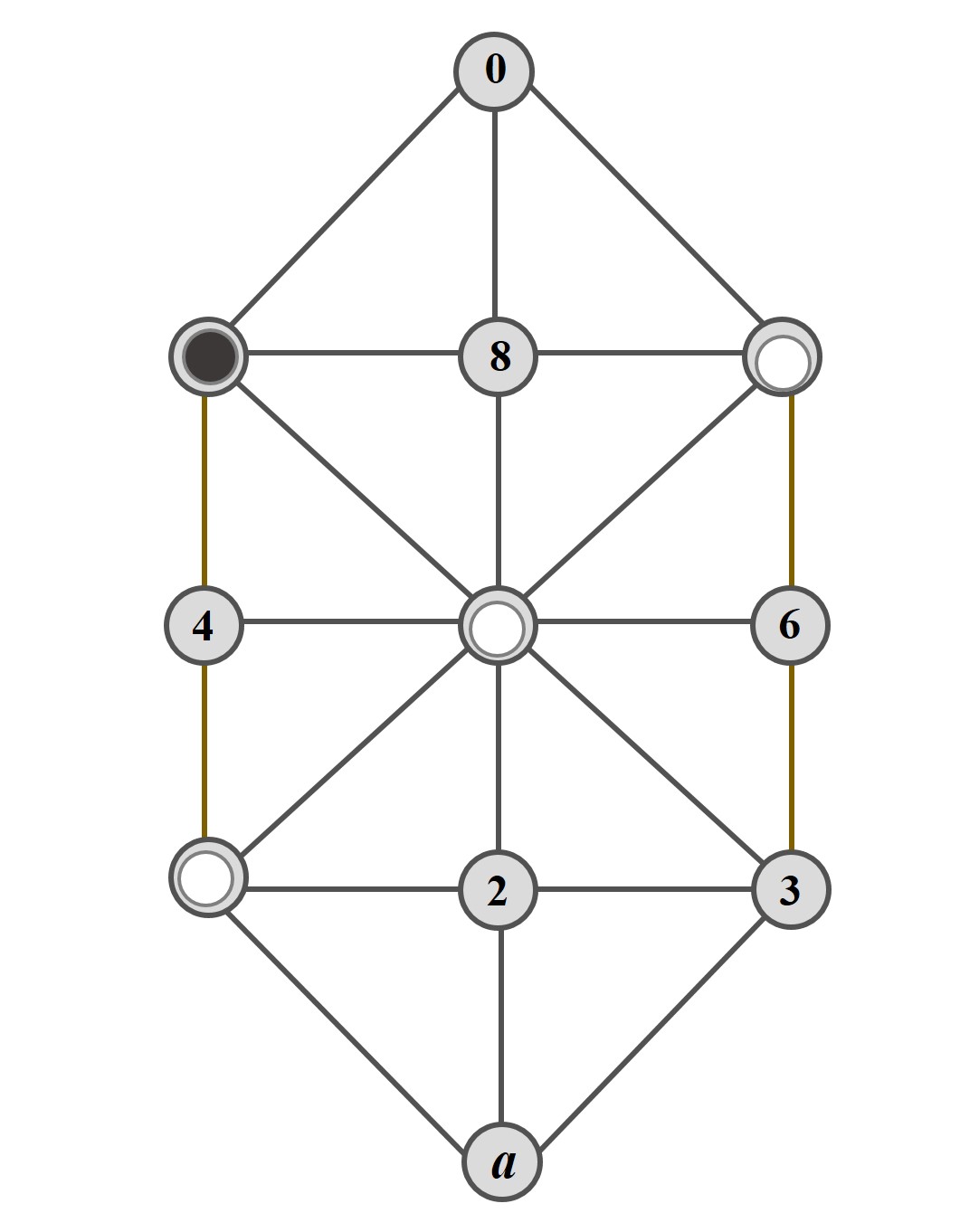
Las dos partidas posibles serían 159 7 459 8 579 0 789 y 159 7 459 0 479 8 579 0 789, que Édouard Lucas denota de la siguiente manera, con una linea vertical, para reflejar las dos opciones de movimiento de la ficha negra.

Como hemos explicado más arriba, en la posición inicial la ficha negra está en la casilla 2, mientras que las fichas blancas están en las casillas a, 1 y 3. El primer movimiento de la ficha negra es obligado, de la casilla 2 a la casilla 5 y ahí las blancas, aunque tienen diferentes opciones deberían mover de la casilla a a la casilla 2. Luego el inicio de la partida sería 2 a13 5 123. En el siguiente recuadro se recoge la tabla del análisis del juego realizada por Lucas para mostrar que ganan las fichas blancas si mueven convenientemente. Las letras, de la A a la F, indican que hemos llegado a la partida elemental con ese nombre, mientras que el símbolo del $ nos indica que más arriba en la tabla ya se ha producido esa situación y que, por tanto, se continúa de igual forma.

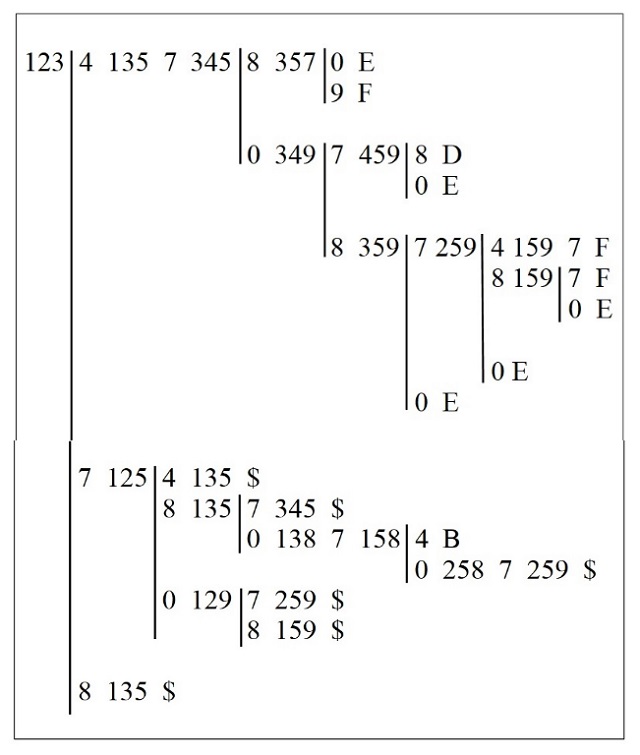
Para comprender bien la estrategia ganadora y disfrutar del análisis de Lucas lo mejor es ir reproduciendo las diferentes jugadas que nos describe el anterior recuadro.

Por cierto, como podemos observar las fichas blancas ganan en doce movimientos como mucho.

Variaciones

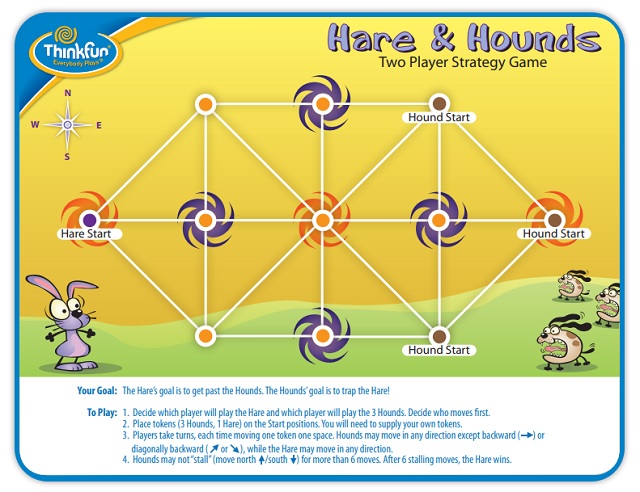
Para terminar podemos plantar algunas variaciones. La primera sería jugar empezando con la ficha negra en otra posición distinta. Por ejemplo, un inicio de partida bastante frecuente es con la ficha negra en el otro lado del tablero, en la casilla 0, y el jugador que empieza primero se decide a suertes o se va cambiando. Por ejemplo, en la siguiente imagen se muestra el tablero de la empresa de juegos Thinkfun que plantea esta alternativa.

Existen diferentes alternativas al tablero del juego. Algunas de las cuales las mostraremos a continuación para quienes estén interesados en jugar a ellas. La primera es un tablero similar al anterior, pero con tan solo 9 casillas, se han eliminado dos de la parte central (véase la siguiente imagen).

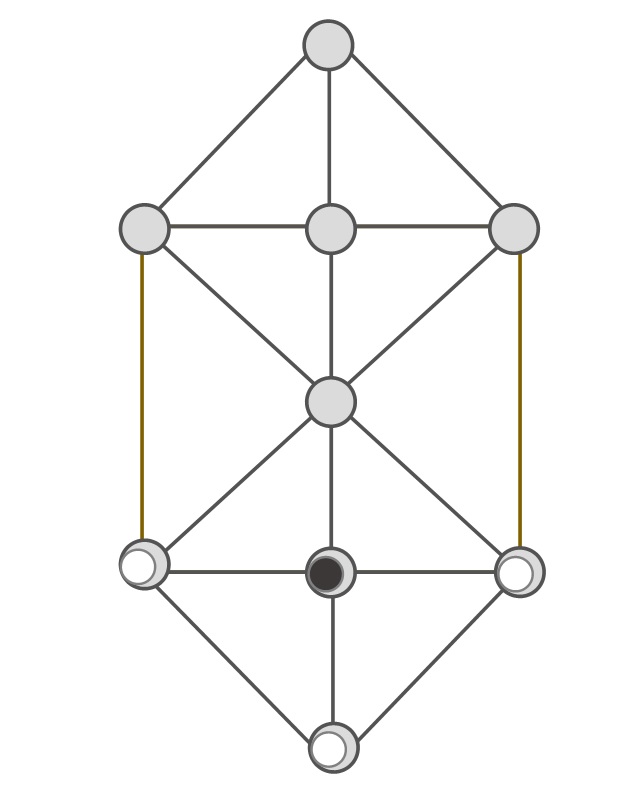
Existe otra versión con 12 casilla, que mostramos en la siguiente imagen.

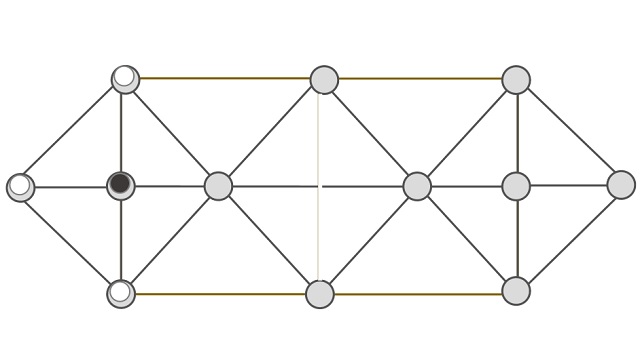
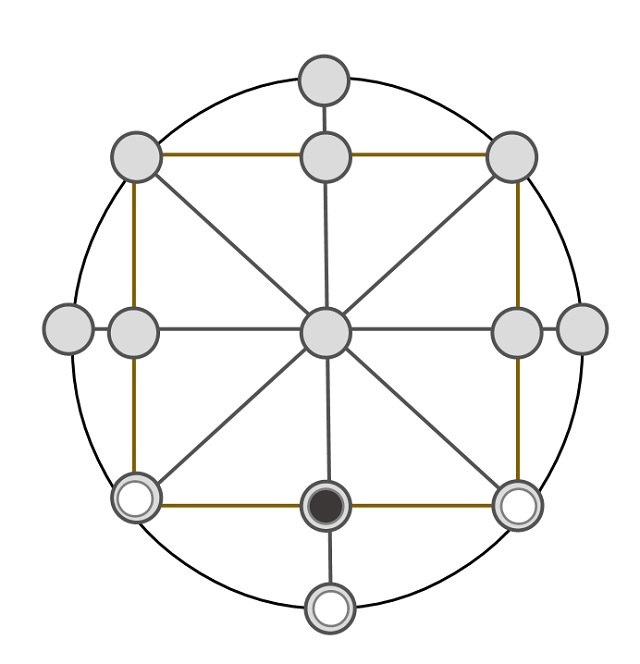
Incluso un tablero circular de 13 puntos (véase la siguiente imagen), entre muchos otros que ya no incluimos en esta entrada.

Bibliografía

1.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.

2.- Peter Michaelsen, Haretavl – Hare and Hounds as a board game, en el libro Sport Und Spiel Bei den Germanen. De Gruyter, pp. 197 – 216, 2013.

3.- Raúl Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.

4.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata, 2023.

5.- Michel Boutin, Les jeux dans les collections du Conservatoire national des arts et métiers, 8-Le Jeu militaire (8e partie), Le Vieux Papier, no. 435, pp 213-222, 2020.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica