Dos investigadores han mejorado una técnica bien conocida para la reducción de bases de retículos, abriendo nuevas vías para experimentos prácticos en criptografía y matemáticas.

Un artículo de Madison Goldberg. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.

En nuestras vidas cada vez más digitales la seguridad depende de la criptografía. Envía un mensaje privado o paga una factura en línea y dependerás de algoritmos diseñados para mantener tus datos secretos. Naturalmente, algunas personas quieren descubrir estos secretos, por lo que los investigadores trabajan para probar la robustez de estos sistemas y asegurarse de que no se desmoronen a manos de un atacante inteligente.

Una herramienta importante en este trabajo es el algoritmo LLL, que lleva el nombre de los investigadores que lo publicaron en 1982: Arjen Lenstra, Hendrik Lenstra Jr. y László Lovász. LLL, junto con sus numerosos descendientes, puede desbaratar ardides criptográficos en algunos casos; estudiar cómo se comportan ayuda a los investigadores a diseñar sistemas que sean menos vulnerables a los ataques. Y los talentos del algoritmo van más allá de la criptografía: también es una herramienta útil en campos matemáticos avanzados como la teoría de números computacional.

A lo largo de los años, los investigadores han perfeccionado variantes de LLL para hacer que el enfoque sea más práctico, pero sólo hasta cierto punto. Ahora, un par de criptógrafos han creado un nuevo algoritmo estilo LLL con un aumento significativo en la eficiencia. La nueva técnica, que ganó el premio al Mejor Artículo en la Conferencia Internacional de Criptología de 2023, amplía la gama de escenarios en los que informáticos y matemáticos pueden utilizar enfoques similares a LLL.

«Fue realmente emocionante», comenta Chris Peikert, criptógrafo de la Universidad de Michigan que no participó en el artículo. La herramienta ha sido objeto de estudio durante décadas, afirma. «Siempre es agradable cuando un objetivo en el que se ha trabajado durante tanto tiempo… demuestra que todavía hay sorpresas por encontrar».

Los algoritmos de tipo LLL operan en el mundo de los retículos: colecciones infinitas de puntos espaciados regularmente. Como una forma de visualizar esto, imagina que estás enbaldosando un suelo. Podrías cubrirlo con baldosas cuadradas y las esquinas de esas baldosas formarían un retículo. Alternativamente, puedes elegir una forma de baldosa diferente (por ejemplo, un paralelogramo alargargado) para crear un retículo diferente.

Un retículo se puede describir utilizando su «base». Esta es un conjunto de vectores (esencialmente, listas de números) que puedes combinar de diferentes maneras para obtener cada punto del retículo. Imaginemos un retículo con una base formada por dos vectores: [3, 2] y [1, 4]. El retículo es simplemente todos los puntos a los que puedes llegar sumando y restando copias de esos vectores.

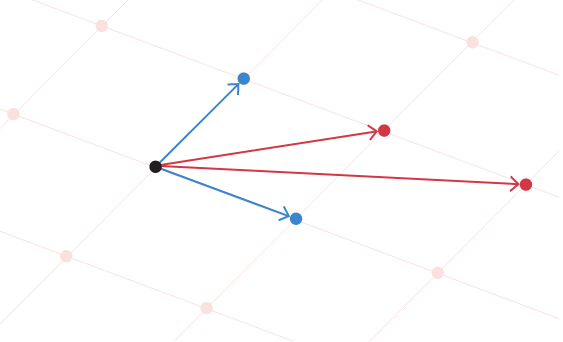
Ese par de vectores no es la única base del retículo. Todo retículo con al menos dos dimensiones tiene infinitas bases posibles. Pero no todas las bases son iguales. Una base cuyos vectores son más cortos y más cercanos a ángulos rectos entre sí suele ser más fácil de trabajar y más útil para resolver algunos problemas computacionales, por lo que los investigadores llaman a esas bases «buenas». Un ejemplo de esto es el par de vectores azules en la siguiente figura. Las bases que consisten en vectores más largos y menos ortogonales, como los vectores rojos, pueden considerarse «malas».

Este es un trabajo para LLL: dale (o a sus hermanos) una base de un retículo multidimensional y encontrará una mejor. Este proceso se conoce como reducción de base de retículos.

¿Qué tiene todo esto que ver con la criptografía? Resulta que la tarea de romper un sistema criptográfico puede, en algunos casos, reformularse como otro problema: encontrar un vector relativamente corto en un retículo. Y, a veces, ese vector se puede extraer de la base reducida generada por un algoritmo de estilo LLL. Esta estrategia ha ayudado a los investigadores a tumbar sistemas que, en apariencia, parecen tener poco que ver con los retículos.

En un sentido teórico, el algoritmo LLL original se ejecuta rápidamente: el tiempo que lleva la ejecución no escala exponencialmente con el tamaño de la entrada, es decir, la dimensión del retículo y el tamaño (en bits) de los números en los vectores de la base. Pero sí aumenta como función polinómica, y “si realmente quieres hacerlo, el tiempo polinómico no siempre es tan factible”, apunta Léo Ducas, criptógrafo del instituto nacional de investigación CWI de los Países Bajos.

En la práctica, esto significa que el algoritmo LLL original no puede manejar entradas demasiado grandes. “Los matemáticos y criptógrafos querían tener la capacidad de hacer más”, dice Keegan Ryan, estudiante de doctorado de la Universidad de California en San Diego. Los investigadores han trabajado para optimizar los algoritmos de estilo LLL para acomodar entradas más grandes, logrando a menudo un buen rendimiento. Aún así, algunas tareas han permanecido obstinadamente fuera de alcance.

El nuevo artículo, escrito por Ryan y su directora de tesis, Nadia Heninger, combina múltiples estrategias para mejorar la eficiencia de su algoritmo estilo LLL. Por un lado, la técnica utiliza una estructura recursiva que divide la tarea en partes más pequeñas. Por otro lado, el algoritmo gestiona cuidadosamente la precisión de los números involucrados, encontrando un equilibrio entre velocidad y un resultado correcto. El nuevo trabajo permite a los investigadores reducir las bases de retículos de miles de dimensiones.

Trabajos anteriores han seguido un enfoque similar: un artículo de 2021 también combina la recursividad y la gestión de la precisión para agilizar el trabajo con retículos grandes, pero funciona solo para tipos específicos de retículos, y no para todos las que son importantes en criptografía. El nuevo algoritmo se comporta bien en un rango mucho más amplio. «Estoy muy feliz de que alguien lo haya hecho», comenta Thomas Espitau, investigador en criptografía de la empresa PQShield y uno de los autores de la versión de 2021. El trabajo de su equipo ofreció una “prueba de concepto”, dice; el nuevo resultado muestra que «se puede realizar una reducción de retículo muy rápida de forma robusta».

La nueva técnica ya ha comenzado a resultar útil. Aurel Page, matemático del instituto nacional de investigación francés INRIA, ha dicho que él y su equipo han puesto en marcha una adaptación del algoritmo en algunas tareas computacionales de teoría de números.

Los algoritmos de estilo LLL también pueden desempeñar un papel en la investigación relacionada con sistemas de criptografía basados en retículos diseñados para permanecer seguros incluso en un futuro con potentes ordenadores cuánticos. No representan una amenaza para estos sistemas, ya que tumbarlos requiere encontrar vectores más cortos que los que estos algoritmos pueden lograr. Pero los mejores ataques que los investigadores conocen utilizan un algoritmo de estilo LLL como “elemento básico”, explica Wessel van Woerden, criptógrafo de la Universidad de Burdeos. En experimentos prácticos para estudiar estos ataques, ese elemento básico puede ralentizarlo todo. Con la nueva herramienta, los investigadores podrán ampliar la gama de experimentos que pueden ejecutar con los algoritmos de ataque, ofreciendo una imagen más clara de su rendimiento.

El artículo original, Celebrated Cryptography Algorithm Gets an Upgrade, se publicó el 14 de diciembre de 2023 en Quanta Magazine.

Traducido por César Tomé López