El pasado 8 de octubre se anunció que el Premio Nobel de Física de este año sería para John J. Hopfield y Geoffrey E. Hinton por sus trabajos en redes neuronales y aprendizaje automático. Para muchos, esto supuso un triple salto mortal del comité de la Academia de Ciencias sueca en un intento por premiar una disciplina, las matemáticas, que no tiene categoría propia; sin embargo, en este caso la física juega un papel más importante del que parece o, al menos, algunos de los modelos matemáticos que rigen determinados fenómenos.

Aunque esto es algo en lo que no siempre se enfatiza demasiado en las asignaturas de Física ―lo que puede llevar a cualquier estudiante a tener un cacao de ecuaciones importante en la cabeza―, fenómenos similares utilizan ecuaciones similares. Esto es: una ecuación de ondas es una ecuación de ondas en mecánica, electromagnetismo o física cuántica, lo que cambia de un ámbito a otro son los «ajustes» que le hacemos. Esto lo explicaba muy bien Richard Feynman en sus populares Lectures poniendo el ejemplo de un oscilador amortiguado mecánico ―un muelle con una masa unida a uno de sus extremos, con rozamiento― y un oscilador eléctrico ―un circuito RLC, con una resistencia, una bobina de inducción y un condensador―: la ecuación que describe ambos sistemas es la misma y, por tanto, se comportan igual.

Física estadística para neuronas

Pensemos en el potencial de esto a la hora de entender el mundo que nos rodea, en varios sentidos. Puede suceder que, por cualquier motivo, no tengamos acceso a determinados datos, recursos… para hacer un experimento, pero sí su análogo. Podemos hacer una sustitución y extrapolar los resultados de uno al otro. Pero también podríamos, una vez descubierta cierta propiedad o comportamiento de un sistema físico, tratar de reproducirlo en otro ámbito. Eso es más o menos lo que hicieron Hopfield y Hinton: ambos aplicaron modelos matemáticos extraídos de la física estadística a su trabajo con redes neuronales.

La física estadística estudia las propiedades de sistemas compuestos por una gran cantidad de partículas. Es una aproximación necesaria en muchos casos ante la imposibilidad de realizar los cálculos componente a componente cuando hay demasiadas y se empezó a utilizar, sobre todo, en el ámbito de la termodinámica y el comportamiento de los gases, para explicar fenómenos como la temperatura o la presión a partir del comportamiento de los átomos o moléculas que los componen. Pero no tiene por qué estar limitada a esto: una red neuronal artificial puede describirse también como un sistema de este tipo. Y tanto Hopfield como Hinton se basaron en la mecánica estadística para desarrollar sus modelos de aprendizaje automático. El primero, en el modelo de Ising del ferromagnetismo; el segundo, en la distribución de Boltzmann.

Hopfield y el modelo de Ising para el ferromagnetismo

El modelo de Ising explica el comportamiento de los materiales ferromagnéticos.¹ A grandes rasgos, explica qué es lo que pasa a nivel atómico para que algunos materiales, como el hierro, presenten propiedades magnéticas bajo determinadas condiciones ―normalmente la presencia de un campo magnético externo―. Pero hay un detalle aún más interesante: cuando «desmagnetizamos» un material de este tipo ―retirando el campo magnético externo, por ejemplo―, suele quedar un campo residual. Se podría considerar que tiene una «memoria» de su historia pasada. Ese «residuo» queda almacenado en la configuración de energía de la red de átomos del material, y es el principio que utiliza la red de Hopfield para aprender patrones.

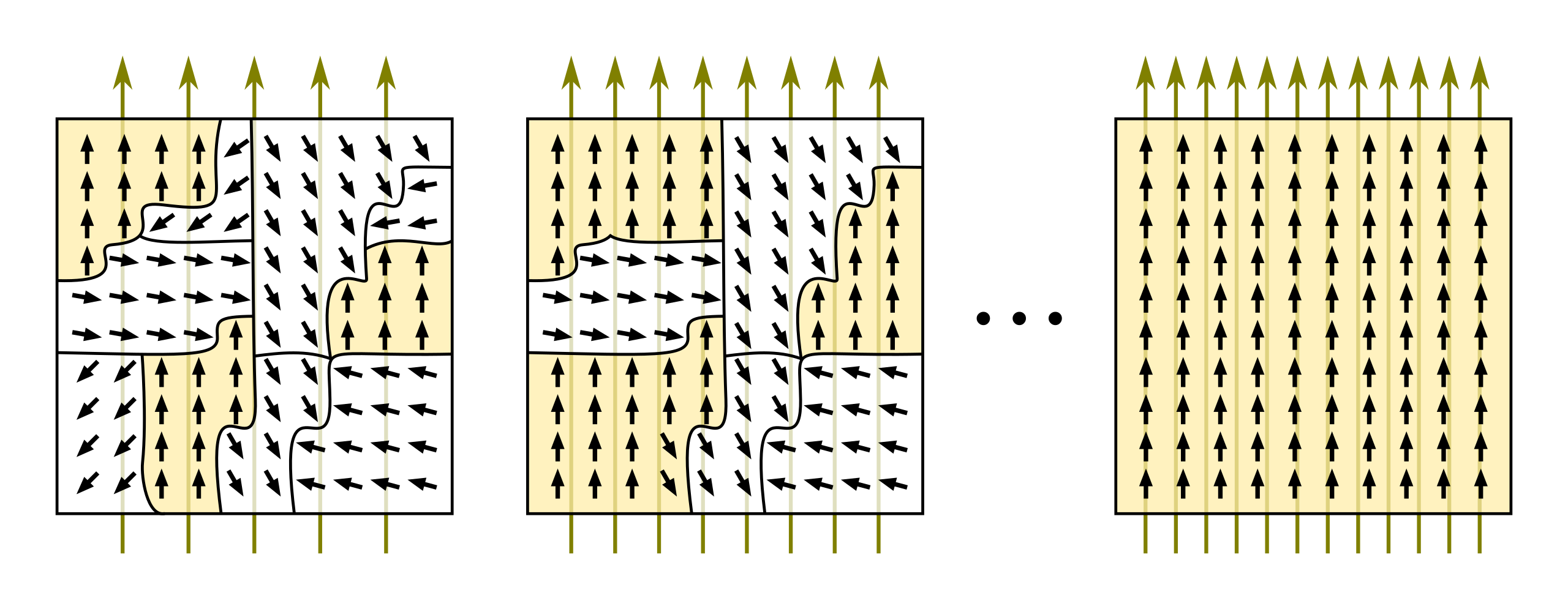
Cambiemos las configuraciones de los espines atómicos ―solo pueden encontrarse en dos estados― del modelo de Ising, que es de donde emergen las propiedades magnéticas del material, por estados de neuronas artificiales, encendido/apagado, y las interacciones entre los espines por pesos sinápticos ―que miden la probabilidad de que una neurona esté activada―, y tendremos una red de Hopfield. ¿Cómo aprende? Reforzando los pesos sinápticos que lleven a configuraciones de baja energía o, en otras palabras, que lleven hacia los patrones de memoria que buscamos.

Hinton y la distribución de Boltzmann

Con las máquinas de Bolztmann de Geoffrey E. Hinton sucede algo similar. Son una extensión de las redes de Hopfield basadas en la distribución de Bolztmann. Por supuesto, el físico austriaco no estaba pensando en inteligencia artificial, sino en cómo interaccionan los átomos en un gas para explicar sus propiedades macroscópicas Una visión que, por otro lado, lo llevó a desarrollar una descripción matemática de la entropía de un sistema y a establecer la dirección preferente de los procesos termodinámicos hacia estados en los que esta es mayor.

La distribución de Boltzmann mide la probabilidad de encontrar un sistema termodinámico ―en equilibrio térmico― en un determinado estado macroscópico en función de los microestados de los átomos o moléculas que lo componen. De nuevo, y como en el modelo de Ising, el punto clave aquí es que un sistema que obedezca esta ecuación tenderá siempre a buscar estados de menor energía, ya que son los que tienen más probabilidad de darse. Y, de nuevo, podemos aplicarlo a ámbitos muy diversos. Eso fue lo que hizo Hinton. Cambiemos moléculas e interacciones por neuronas y pesos sinápticos.

Con esta perspectiva, en la que ni siquiera se ha mencionado ante qué tipos de redes neuronales nos encontramos, ni hemos hablado de algoritmos ni informática, ya podemos volver a preguntarnos si la física está relacionada o no con el Premio Nobel de este año.

Tengamos en cuenta algo más, ¿no intenta la inteligencia artificial simular el comportamiento humano? ¿Y no forman parte los seres humanos de un universo regido por determinadas leyes? No parece tan descabellado inspirarnos, por tanto, en modelos que ya conocemos, ¿no?

…y la psicohistoria

En el caso concreto de la distribución de Boltzmann, sus aplicaciones a otros ámbitos están por todas partes. Se utiliza en química, en biología, en economía, en sistemas complejos… se utilizó hasta en ciencia ficción. La psicohistoria de Isaac Asimov no es más que el estudio del comportamiento de una sociedad a partir de los comportamientos individuales de sus ciudadanos siguiendo el modelo estadístico de Boltzmann: normalmente tendemos a buscar estados estables, de baja energía, aunque también es posible que un elemento disruptivo como el Mulo u otro tipo de inestabilidades económicas, culturales, etc., rompan el equilibrio. Lo que cabría plantearse ahora es que si las máquinas de Boltzmann de Hinton y la psicohistoria de Asimov siguen el mismo principio, ¿es posible entonces que Hari Seldon fuera el entrenador de una red neuronal galáctica?

Bibliografía

Ackley, D. H.; Hinton, G. E. y Sejnowski, T. J. (1985). A learning algorithm for bolztmann machines. Cognitive Science,9(1), 147-169.

Baños, G. (2024). El sueño de la inteligencia artificial. Shackleton Books.

Feynman, R. (2010 [1963]). The Feynman Lectures on Physics. Volume I: Mainly mechanis, radiation and heat. The New Millenium Edition. Basic Books.

Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational habilities. Proc. Natl. Acad. Sci. USA, 79.

The Royal Swedish Academy of Sciences (2024). The Nobel Prize in Physics 2024. https://www.nobelprize.org/prizes/physics/2024/summary

Nota:

.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.