El 25 de noviembre de 2019, la UNESCO proclamó oficialmente el 14 de marzo como el Día Internacional de las Matemáticas, con el fin de consolidar “el reconocimiento a las matemáticas por su importante papel para hacer frente a los desafíos de nuestro tiempo en ámbitos como la inteligencia artificial, la salud, el cambio climático, la energía y el desarrollo sostenible y la mejora de la calidad de vida de la sociedad en general”.

La elección del 14 de marzo como Día Internacional de las Matemáticas se debió a que el 14 de marzo, es decir, 3/14 en inglés, ya era un día de celebración matemática en muchos lugares del mundo, el conocido y popular Día de Pi. El Día de Pi se celebra desde el año 1988, a partir de la idea propuesta por el físico y artista estadounidense Larry Shaw (1939-2017), que se apoyaba en la coincidencia con la fecha del cumpleaños del físico germano-estadounidense Albert Einstein (1879-1955). También esa fecha, 14 de marzo, es el aniversario del nacimiento de un gran matemático, el polaco Wlaclaw Sierpinski (1882-1969), aunque prácticamente desconocido fuera de las matemáticas, salvo por los fractales que llevan su nombre.

El número pi, que designamos con la letra griega π, es una de las constantes matemáticas más importantes que existen, pero además es un número fascinante que goza de una gran popularidad entre el público, matemático y no matemático. Como decíamos en la entrada del Cuaderno de Cultura Científica ¿Es normal el número pi?, parte de la magia de este número es que aparece en los lugares más insospechados, y tiene infinidad de aplicaciones, aunque como muchas otras constantes matemáticas. En todas las ramas de las matemáticas, desde la geometría hasta la probabilidad, pasando por la teoría de números, en física (en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb de la electricidad), en geología (para estimar la longitud de los ríos, debido a que relaciona dicha longitud con la distancia directa del nacimiento del río a su desembocadura), en bioquímica (en el estudio de la estructura de una molécula de ADN), en astronomía (en la búsqueda de exo-planetas o el estudio de la forma del universo), y muchas aplicaciones más en navegación, análisis de señales, dinámica de poblaciones o ingeniería, incluso en deporte (para calcular las posiciones de salida en las pistas de una carrera de atletismo, como vimos en la entrada Pi atleta).

El número π

El número π es la proporción entre la longitud de una circunferencia (perímetro del círculo) y su diámetro.

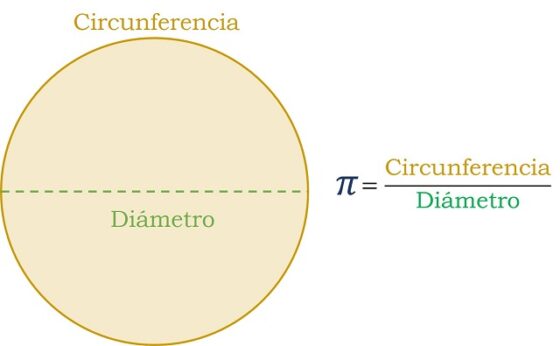
Desde la antigüedad se han realizado aproximaciones a esta proporción. Una aproximación muy sencilla que fue muy utilizada en la antigüedad es la que asigna a esta proporción, el número π, el valor de 3. Así ocurre en la Biblia, en el Antiguo Testamento. Exactamente en el Libro Primero de los Reyes (7:23), escrito en el siglo VI a.n.e., al narrarse la construcción del Palacio de Salomón se puede leer lo siguiente:

Hizo el Mar [gran depósito cilíndrico de agua] de metal fundido que tenía 10 codos de borde a borde; era enteramente redondo, y de cinco codos de altura; un cordón de treinta codos medía su contorno.

Es decir, se está estableciendo que la razón entre la longitud de la circunferencia del cilindro (30 codos) y el diámetro (10 codos) es 3, luego este el valor considerado para π (C/D) en la Biblia.

El número π en Babilonia

En algunas tablillas de arcilla babilónicas, como la tablilla YBC 7302 (aprox. 1.900-1.600 a.n.e.) que se muestra en la siguiente imagen, se observa que ese valor también era utilizado por los babilonios mucho tiempo antes.

Según los estudios sobre las matemáticas de algunas tablillas de arcilla babilónicas (véase, por ejemplo, el libro A History of Mathematics, An Introduction, de Victor J. Katz) los babilonios utilizaban la longitud de la circunferencia (C) como referencia de las medidas del círculo, considerando que el diámetro tomaba el valor de 1/3 de la longitud de su circunferencia (lo cual es equivalente a darle al número π el valor de 3) y el área 1/12 del cuadrado de la longitud de su circunferencia. Así, los números que aparecen en la tablilla YBC 7302, que son 3, 9 y 45, tienen el siguiente significado: 3 es la longitud de la circunferencia, 9 es su cuadrado y el área, que sería 9/12, es el número que aparece dentro del círculo, que si tenemos en cuenta que los babilonios trabajaban con el sistema de numeración posicional en base 60 (en la entrada ¿Sueñan los babilonios con multiplicaciones eléctricas? podéis leer sobre el sistema de numeración posicional en base 60 de los babilonios, aunque para números naturales; en el libro Los secretos de la multiplicación podéis leer también sobre este sistema de numeración, tanto para los números naturales, como para los números con decimales) y que el número 9/12 = 3/4 se representaba en el sistema de numeración sexagesimal babilónico como 0;45, se obtiene el 45 que está en el centro del círculo.

Aunque en 1933 se encontró una tablilla de arcilla en la ciudad de Susa (1.900-1.600 a.n.e.) con una mejor estimación para el número π. En esta tablilla babilónica, SB 13088, se establece una relación entre el perímetro de un hexágono regular y el perímetro de la circunferencia circunscrita. En concreto, dentro del hexágono está escrito que esa relación es [0; 57; 36] en su sistema sexagesimal, que en el sistema decimal sería 57/60 + 36/60² = 0,96.

Si tenemos en cuenta que en un hexágono de lado r tiene un perímetro igual a 6r y que el perímetro de la circunferencia circunscrita al hexágono, cuyo radio es también r, es 2πr, entonces que la relación entre ambos perímetros 6r/2πr = 3/π sea igual a 0,96, lleva a deducir que π toma el valor aproximado de 25 / 8 = 3 + 1/8 = 3,125.

El número π en el Antiguo Egipto

Aunque la primera aproximación al valor de esta constante matemática de la que se tiene constancia nos remite al Antiguo Egipto, en concreto, al Papiro Matemático de Rhind.

El Papiro Matemático de Rhind es una de las muchas joyas del British Museum / Museo Británico, de Londres. Como se puede leer en la descripción que hace el museo del mismo:

El papiro es probablemente un libro de texto de matemáticas, utilizado por los escribas para aprender a resolver problemas matemáticos concretos escribiendo ejemplos apropiados. El texto incluye ochenta y cuatro problemas que abarcan tablas de divisiones, multiplicaciones y manejo de fracciones, así como geometría, incluyendo volúmenes y áreas. El escriba Ahmes lo fechó en el año 33 de Apofis I, el penúltimo rey de la dinastía XV de Egipto.

Debido a que el propio escriba establece que ese documento fue escrito el año 33 del faraón Apofis I (aprox. c. 1583-1522 a.n.e.) de la dinastía XV de Egipto, se ha estimado que su escritura tuvo lugar alrededor del año 1.550 a.n.e. Además, este escriba también afirma que ese documento es una copia de un documento más antiguo, de la época del faraón Amenemhat III (aprox. 1849-1801) de la dinastía XII de Egipto.

Respecto al contenido del Papiro Matemático de Rhind, como se comentaba en la descripción, está compuesto de ochenta y cuatro problemas. Son problemas de diferentes tipos, sobre operaciones aritméticas con números enteros y fracciones, resolución de ecuaciones de primer grado, áreas y volúmenes, inclinación de pirámides, reparto de bienes, proporciones aritméticas y geométricas, incluso problemas de ingenio. En particular, entre los problemas de áreas, que son el grupo de problemas entre el 48 y el 55, hay dos que tienen que ver con el área del círculo y su circunferencia, luego con nuestra importante constante matemática, los problemas 48 y 50, que van a ser analizados en los siguientes apartados de esta entrada del Cuaderno de Cultura Científica.

Problema 50 del Papiro Matemático de Rhind

Vayamos con los dos problemas relacionados con el cálculo del área de un círculo. Los textos de estos problemas y sus soluciones se han tomado de la publicación The Rhind Mathematical Papyrus: British Museum 10057 and 10058.

Empezaremos por el problema 50, que vemos en la siguiente imagen.

La transcripción del texto que aparece en la imagen (problema 50) es la siguiente.

Problema 50: Ejemplo de un campo redondo de 9 khet [el khet era una unidad de medida del Antiguo Egipto, que eran 100 codos, lo que en medidas modernas serían entre 52,3 y 52,6 metros] de diámetro. ¿Cuál es su área?

Quita 1/9 del diámetro, es decir, 1; el resto es 8. Multiplica 8 por 8; el resultado es 64. Por lo tanto, contiene 64 setat [el setat es una unidad de área y 1 setat es igual al área de un cuadrado de lado 1 khet] de tierra.

Hazlo así:

Imagen 9

quitado esto nos queda 8

Imagen 10

Su área es 64 setat.

Como se observa, primero aparece el texto del problema, seguido de su solución y, por último, se muestra cómo realizar las operaciones aritméticas que plantea la solución para obtener el resultado final.

Analicemos brevemente en qué consiste la solución. Supongamos que nuestro campo circular tiene un diámetro de D unidades (9 khet en el problema del papiro), entonces la solución plantea que se calcule 1/9 del diámetro (1/9 D), se quite esta cantidad al diámetro (D – 1/9 D) y se eleve esta cantidad al cuadrado (que es como calcular el área del cuadrado de lado D – 1/9 D), obteniendo de esta forma el área (una aproximación) del campo circular:

Área círculo = (D – 1/9 D)² = (8/9 D)².

Si tenemos en cuenta la fórmula del área de un círculo, que hemos estudiado en la escuela, Área = π R², siendo el radio R igual a la mitad del diámetro D, se obtiene que, en la anterior solución del Papiro Matemático de Rhind, se está realizando la siguiente aproximación del número π:

π = 256/81 = 3 + 13/81 = 3,1604938272…

o simplificando, 3,16, una aproximación de hace unos 4.000 años nada menos.

Problema 48 del Papiro Matemático de Rhind

Para entender el motivo por el cual se elige esa aproximación del área del círculo, que conlleva la aproximación comentada del número π, tenemos que mirar ahora al problema 48.

Problema 48: Compara el área de un círculo y la del cuadrado circunscrito al mismo.

Como podemos observar en la respuesta, el área del cuadrado de lado 9 khet es 81 setat, lo cual está claro, ya que el área del cuadrado era de sobra conocido en el Antiguo Egipto, mientras que, como en el problema 50, se aproxima el área del círculo de diámetro 9 con un cuadrado de lado 8 (8² = 64).

Para entender cómo llegan a esa aproximación para el área del círculo, tenemos que observar la imagen que acompaña a la solución del problema 48, que es la que se muestra a continuación.

Como se puede observar en la imagen, se aproxima el círculo de diámetro 9 mediante un octógono. A continuación, vamos a representar juntos, el cuadrado de lado 9, el círculo de diámetro 9 y un octógono que lo aproxima. Además, intentaremos dar una explicación de la aproximación sencilla que aparece en el Papiro Matemático del Rhind del área del círculo, utilizando el octógono que nos sugiere la imagen anterior.

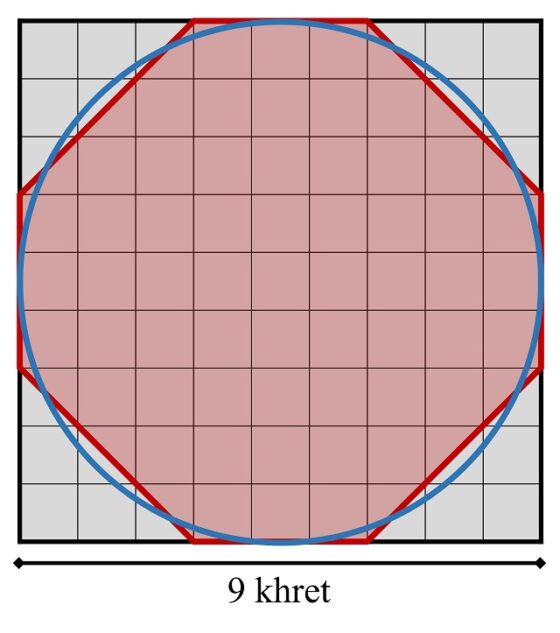
Por lo tanto, el área del círculo lo podríamos aproximar mediante el área del octógono. Pero si nos fijamos, el área del octógono es el área del cuadrado, menos el área de las cuatro esquinas que están en el cuadrado, pero no en el octógono, y cada una de esas esquinas tiene un área de 4,5 cuadraditos (satet), tres cuadraditos enteros y tres mitades de cuadraditos (3 + 1,5). Por lo tanto, el área del octógono sería 81 cuadraditos (satet) menos 4 veces 4,5 cuadraditos (satet), es decir, 81 – 18 = 63 cuadraditos (satet), resultado próximo a los 64 cuadraditos (satet), que es la solución dada en el problema.

Si al cuadrado anterior, de lado 9 khet, le quitamos una fila y una columna (en total, 17 cuadrados, ya que se comparte un cuadradito), queda un cuadrado de lado 8, cuya área aproxima el área del octógono (64 frente a 63).

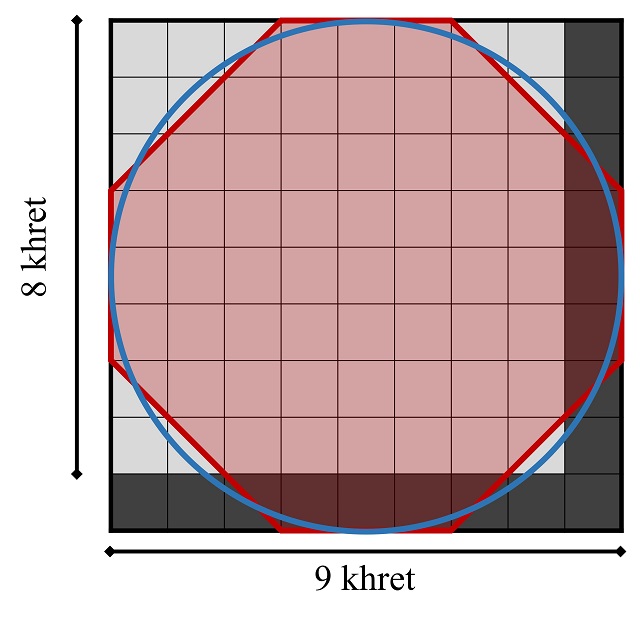
Por lo tanto, en la antigüedad ya se realizaron algunas aproximaciones interesantes del número π, la proporción entre la longitud de una circunferencia (perímetro) y su diámetro, como el valor 25/8 = 3,125 en Babilonia o 256/81 = 3 + 13/81 = 3,1604938272… en el Antiguo Egipto.

Bibliografía:

1.- Victor J. Katz, A History of Mathematics, An Introduction, Addison-Wesley, 2009.

2.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Editorial Los libros de la Catarata, 2019.

3.- Jörg Arndt, Christoph Haenel, Pi – Unleashed, Springer, 2001.

4.- Petr Beckmann, A History of Pi, St. Martin Press, 1971.

5.- Arnold Buffum Chace, Ludlow Bull, Henry Parker Manning, The Rhind Mathematical Papyrus: British Museum 10057 and 10058, Mathematical Association of America, 1927 (vol. I), 1929 (vol. II).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica