A ninguna de las personas que lea habitualmente los artículos del Cuaderno de Cultura Científica, en particular, los pertenecientes a la sección Matemoción, le sorprenderá la afirmación de que el diseñador, artista polifacético y educador suizo Max Bill (1908-1994), figura central de arte concreto, utilizó las matemáticas (teorema de Pitágoras, banda de Moebius, figuras geométricas planas –polígonos, círculos y otras curvas- y espaciales –esferas, toros y poliedros-, el hipercubo, sucesiones de números, combinatoria, etcétera) como herramienta de creación artística.

En esta entrada vamos a centrarnos en una serie de obras de este artista concreto que consisten en rombos con ángulo interior recto, es decir, cuadrados girados con un vértice hacia arriba y otro hacia abajo, que están divididos en diferentes triángulos, como la pintura que mostramos más abajo. Más aún, vamos a reflexionar sobre el área de algunos de esos triángulos, cuestión fundamental en el proceso creativo de las mismas, como podemos apreciar por el título de la siguiente obra, Unidad de colores con la misma superficie (1972), que fue expuesta en la Fundación Juan March dentro de la exposición Max Bill (2015).

Además, la herramienta que vamos a utilizar para analizar estas obras es muy sencilla, se trata de la fórmula del área de un triángulo, esto es, “base por altura, dividido por dos”.
La fórmula del área de un triángulo
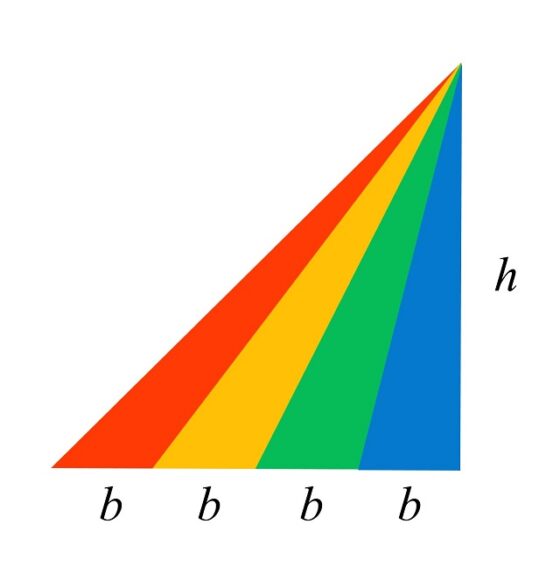
La fórmula clásica para calcular el área de un triángulo es muy sencilla y fácil de demostrar. Para calcular el área de un triángulo solo se necesita conocer la longitud de uno de los lados del triángulo, que vamos a tomar como su base (el lado horizontal en la siguiente imagen), y la de su altura, es decir, del segmento perpendicular a la base (o a su prolongación) que la une con el vértice opuesto. Entonces, el área está dada por la expresión matemática “(longitud de la) base por (longitud de la) altura, dividido por dos”, como se muestra en la siguiente imagen.
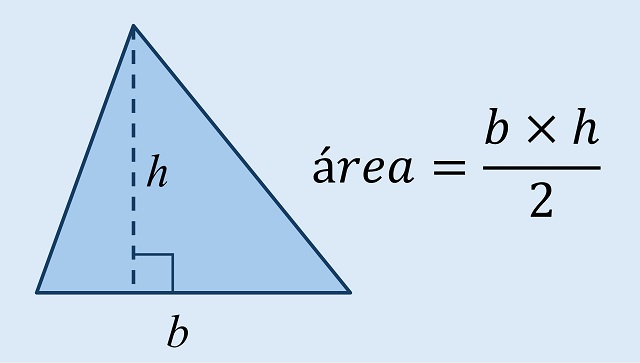
Además de la sencillez de la fórmula, esta es fácil de entender y demostrar. La demostración consiste en duplicar el triángulo, juntar las dos partes para construir un paralelogramo, que de forma sencilla se transforma en un rectángulo de las mismas base y altura que el triángulo original. En consecuencia, su área, el doble que la del triángulo original, es igual al producto de la base por la altura, como se muestra en la siguiente imagen.
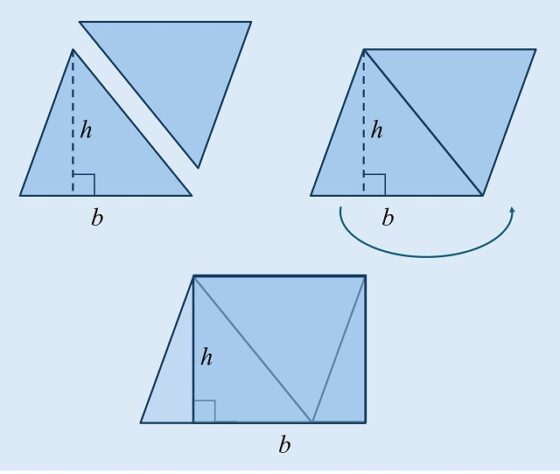
Una cuestión para tener en cuenta es que la base del triángulo puede ser cualquiera de sus tres lados, cada uno de los cuales tendrá asociada una altura diferente, de lo que se desprende que se tienen tres expresiones distintas, auque emanan de la misma fórmula, que proporcionan el área del triángulo. En la siguiente imagen se muestran las tres expresiones para un triángulo ABC.
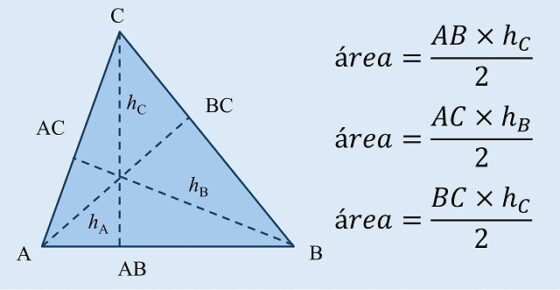
En el ejemplo del triángulo anterior, las tres alturas son interiores, están dentro del triángulo. Sin embargo, la altura puede ser también uno de los lados, si el triángulo es rectángulo, o estar fuera del triángulo, cuando el ángulo es obtuso, mayor de 90 grados, en cuyo caso la altura une un vértice con la prolongación del lado opuesto al mismo.
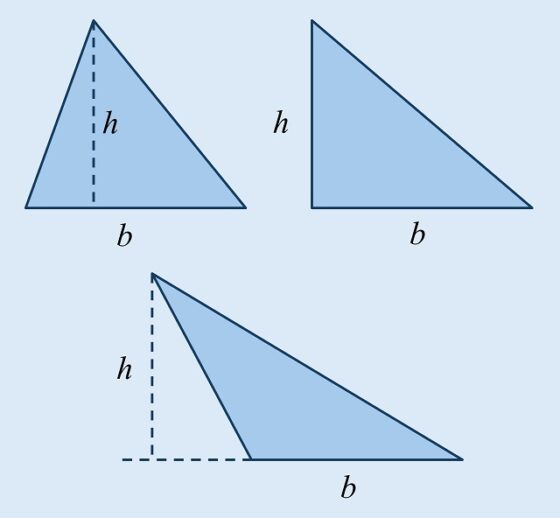
Esta sencilla y clásica fórmula para calcular el área de un triángulo es muy antigua, podemos decir que tan antigua como la propia geometría, ya la conocían en Mesopotamia, el Antiguo Egipto, la Antigua China o la Grecia Clásica.
Los triángulos de Max Bill con la misma superficie
Antes de analizar la pintura al óleo Unidad de colores con la misma superficie (1972), de Max Bill, mencionada en la introducción de esta entrada, analizaremos un par de obras más sencillas, que se citan en el libro Las matemáticas como herramienta de creación artística (Catarata-FESPM, 2023).
La primera es la serigrafía Reflejos triangulares (1972), que como se muestra en la siguiente imagen, es un rombo cuadrado formado por triángulos generados al unir un vértice lateral del rombo con puntos igualmente espaciados en un lado opuesto.

Todos los triángulos de esta obra, cuyos colores son azul, verde, amarillo y rojo, cuatro en la parte superior, sobre la horizontal central (diagonal del cuadrado), y cuatro en la parte inferior, tienen la misma superficie. Para probar esto, vamos a fijarnos solo en los cuatro que están en la parte superior, que son esencialmente iguales a los de la parte inferior.
Si rotamos la parte superior del cuadrado de manera que los lados de este sean verticales y horizontales, como en la siguiente imagen, podemos observar que la altura de los cuatro triángulos es la misma, mientras que las bases, aunque sean distintas, tienen la misma longitud. En conclusión, los cuatro triángulos tienen la misma superficie.
A continuación, se analiza la serigrafía 12 triángulos de cantidades iguales en el cuadrado (1990). Esta obra formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015. Podéis verla en su catálogo, al que se puede acceder online, y que es esencialmente la misma que la que aparece en la siguiente imagen.

Para ver que todos los triángulos que aparecen en esta obra tienen la misma área, a pesar de que son bastante diferentes unos de otros, vamos a ir por partes. Para empezar, solo consideraremos los seis triángulos de la parte superior, que se pueden juntar de dos en dos formando tres triángulos, como aparecen en la siguiente imagen, que son isoareales, puesto que, como los mostrados en la anterior obra, “tienen la misma base y altura”.
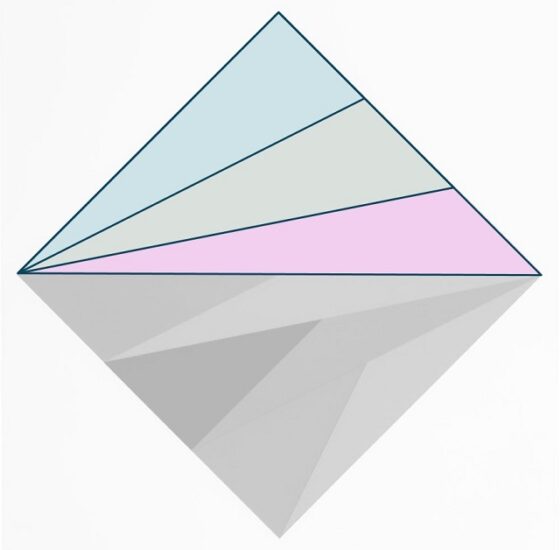
Ahora, cada uno de esos tres triángulos está dividido, a su vez, en dos triángulos más pequeños de la misma superficie. Esta división se realiza trazando un segmento que va del vértice superior al punto medio del lado opuesto, lo que va a garantizarnos que los dos triángulos tienen la misma área, lo cual se deduce utilizando, de nuevo, la fórmula del área de un triángulo.
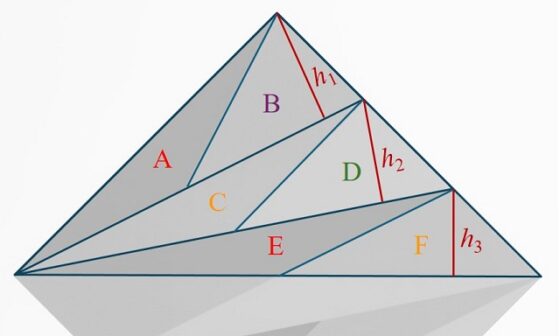
Así, el triángulo de arriba del todo (azul claro) se divide en los triángulos A y B, como se muestra en la siguiente imagen, dos triángulos que tienen sus bases de la misma longitud y que comparten la altura h1, por lo tanto, al calcular “base por altura partido por dos” se obtiene el mismo resultado. Lo mismo ocurre para los otros dos triángulos (verde y morado claros).
Unidad de colores con la misma superficie
Analicemos, a continuación, la obra de Max Bill titulada Unidad de colores con la misma superficie (1972), con la que empezábamos esta entrada. En esta ocasión, vamos a darle la vuelta al análisis y vamos a plantearlo como un reto matemático.
Para empezar, el cuadrado de esta obra mide 120 centímetros de lado. Además, uno de los lados está dividido en dos partes de longitudes (a, b) y el otro en tres partes de longitudes (x, y, z), de manera que cada mitad del cuadrado (arriba y abajo) está dividida en cuatro triángulos (azul, verde, naranja y rojo) con la misma superficie.

Entonces, podemos plantearnos el siguiente problema.
Problema: ¿Cómo se han dividido los lados del cuadrado, es decir, cuánto valen las longitudes x, y, z, a y b, para que los triángulos que se generan en esta pintura tengan efectivamente la misma superficie, si el lado del cuadrado mide 120 centímetros?
Tengamos en cuenta que esto fue lo que se tuvo que plantear el artista Max Bill a la hora de realizar esta obra, para dividir los lados del cuadrado de manera que se cumpliera lo que establece el título.
Resolvamos este sencillo problema en tres etapas.
- Como los triángulos azul y verde (de la parte superior) tienen base x e y, respectivamente, y la altura es la misma para ambos, b, entonces el hecho de que tengan la misma área implica que x = y.
- El triángulo formado por la unión de los triángulos azul y verde, cuya base es b y su altura es x + y, tiene el doble de superficie que el triángulo naranja, que tiene base a y altura x + y, de donde se concluye que b = 2a.
- El triángulo formado por la unión de los triángulos azul, verde y naranja, con base x + y y altura a + b, tiene el triple de superficie que el triángulo rojo, cuya base es z y altura a + b, luego se concluye que x + y = 3z. Como x = y, puede decirse también que 2x = 3z.
Ahora, si denotamos por L la longitud del cuadrado, que sabemos que es 120 centímetros, se tiene que a = L/3 (40 cm), b = 2L/3 (80 cm), x = 3L/8 (45 cm), y = 3L/8 (45 cm), z = L/4 (30 cm).
Los triángulos de Max Bill con distinta superficie
La última parte de esta entrada la vamos a dedicar a un par de obras en las cuales las áreas de los triángulos, aunque diferentes, están relacionadas mediante una sucesión de proporciones.
Otra obra que formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015, fue la litografía Irradiación (1973).

Esta pieza, cuyo cuadrado está en una posición habitual, es decir, los lados están en vertical y horizontal, está formada por tres tipos de triángulos, cada uno de los cuales aparece en las cuatro pequeñas regiones cuadradas en las que podemos dividir el cuadrado de la litografía. Además, cada color (amarillo, verde claro, azul y verde oscuro) comparte un triángulo de cada tipo, luego la superficie de cada color es la misma.
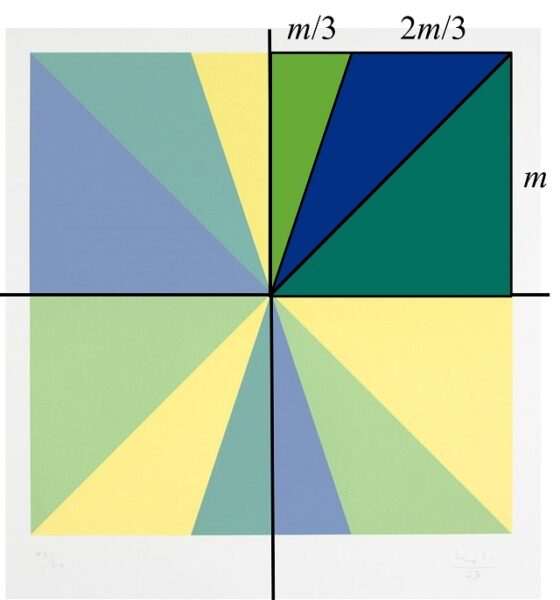
Veamos cual es la relación entre las superficies de los tres tipos de triángulos. Para ello nos fijamos en los triángulos de uno de los pequeños cuadrados, como se muestra en la anterior imagen. Podemos considerar que sus bases tienen longitudes m/3, 2m/3 y m (si el lado del cuadrado mide 2m), mientras que las alturas correspondientes a esas bases tienen la misma longitud en los tres casos, m. De nuevo, calculamos las áreas de estos tres triángulos mediante la sencilla fórmula, obteniendo los valores m2/6, 2m2/6 y m2/2, es decir, la cantidad m2/6 multiplicada por la sucesión de proporciones 1, 2 y 3. Por lo tanto, el triángulo mediano tiene el doble de superficie que el triángulo pequeño, mientras que el grande tiene el triple.
La última obra es la pintura al óleo que aparece con el título Irradiación generada por cuatro de color cuanta idéntico (1972-1973) en el catálogo de la exposición Max Bill que tuvo lugar en el Museo Español de Arte Contemporáneo (Madrid), en 1980, monografía que contiene el interesante artículo de Max Bill titulado La concepción matemática en el arte de nuestro tiempo (de 1949).

Esta pieza, como ocurría con la anterior litografía, Irradiación (1973), está compuesta por triángulos con un vértice común en el centro del rombo cuadrado, como una irradiación de rayos de luz que emanan de ese centro. Son treinta y seis triángulos, de los cuales nueve se apoyan en cada uno de los lados, de distintos tamaños y distintos colores (azul, verde, amarillo y rojo). Los curioso de este óleo es que las superficies de los nueve triángulos que se apoyan en cada lado está relacionadas con la sucesión de Fibonacci (véanse las entradas Fibonacci está en todas partes (I), Fibonacci está en todas partes (II) y Fibonacci está en todas partes (III)), más concretamente, si tomamos como área unidad el del triángulo más pequeño, que se apoya en uno de los vértices del rombo, entonces las áreas de los nueve triángulos toman los nueve primeros valores de la sucesión de Fibonacci
1, 2, 3, 5, 8, 13, 21, 34, 55.
Esto se debe a que los nueve triángulos tienen la misma altura, trazada desde el centro del rombo, pero las bases tienen la particularidad de que la longitud de cada base es igual a la suma de las longitudes de las bases de los dos triángulos anteriores (en el sentido contrario a las agujas del reloj).

Bibliografía
1.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.
2.- Max Bill, El pensamiento matemático del arte de nuestro tiempo, 1949.
3.- Valentina Anker, Max Bill ou la recherche d´un art logique, Editions l´Age d´Homme, 1979
4.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Museu Fundación Juan March, Palma (febrero-mayo 2015) y Museo de Arte Abstracto Español, Cuenca (junio-septiembre, 2015). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
5.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Fundación Juan March, Madrid (octubre 2015 – enero 2016). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
6.- Catálogo de la exposición Max Bill, Museo Español de Arte Contemporáneo, Madrid, Ministerio de Cultura / Dirección General de Patrimonio Artístico, Archivos y Museos, Febrero 1980.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
