Cada fórmula química define un compuesto a partir de los diferentes átomos que contiene. En 1811, el químico francés Joseph Louis Gay-Lussac (1778-1850) observó que existían sustancias distintas que poseían la misma composición química, por lo que sus átomos tendrían que estar enlazados de diferente manera.
En 1823, el químico alemán Justus von Liebig (1803-1873) –que trabajaba en un laboratorio privado con Gay-Lussac– demostró que el fulminato de plata y el cianato de plata –ambos formados por moléculas conteniendo un átomo de plata, uno de carbono, uno de oxígeno y otro de nitrógeno– tenían propiedades muy distintas, en particular, el primero era muy explosivo. ¿Qué los distinguía? Si sus moléculas constaban de los mismos átomos y en la misma cantidad, la diferencia debía residir en la manera en que esos átomos se enlazaban en cada molécula: el fulminato de plata puede escribirse como AgNCO y el cianato de plata es AgOCN.
Gay-Lussac comunicó estos estudios al químico sueco Jöns Jacob von Berzelius (1779-1848). Por su cuenta, Berzelius había descubierto que el ácido racémicoy el ácido tartárico parecían tener la misma fórmula empírica –G4H6O6–, pero no compartían las mismas propiedades; Berzelius sugirió denominarlos isómeros.
En 1857, el polímata británico Arthur Cayley (1821-1895) –y gran experto en teoría de grafos– decidió utilizar sus conocimientos matemáticos en el estudio de los isómeros de alcanos, de fórmula CnH2n+2: deseaba enumerar todas las posibles configuraciones. Su manera de abordar el problema fue la de asignar a cada alcano un árbol –es decir, un grafo, un conjunto de vértices y aristas uniendo algunos de ellos, en el que dos vértices están conectados por exactamente un camino de aristas–. Dado un alcano, Cayley ignoraba los átomos de hidrógeno, y construía un árbol tomando como vértices los átomos de carbono y como aristas los enlaces entre ellos. Su teoría dependía del número de ‘centros’ del alcano. ¿Qué es un centro? Dado el árbol de Cayley –construido a partir de la fórmula del isómero, como acabamos de indicar–, se suprimen los vértices de valencia 1 –la valencia de un vértice es el número de aristas que salen de él–. Cayley demostró que los árboles asociados a alcanos tenían siempre vértices de valencia menor o igual a 4, y que sólo podían tener uno o dos centros.
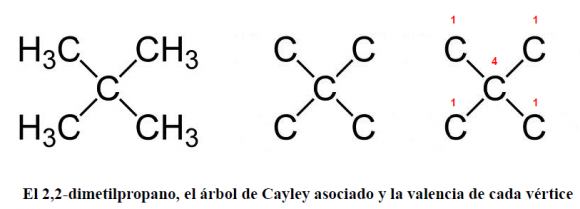
Veamos un ejemplo para entender mejor el concepto de centro y el resultado probado por Cayley: tomemos dos isómeros del alcano con 5 átomos de carbono, el pentano –de fórmula bruta C5H12–.
1. el 2,2-dimetilpropano –C(CH3)4– posee cuatro vértices de valencia 1 y uno de valencia 4, que es su único centro:
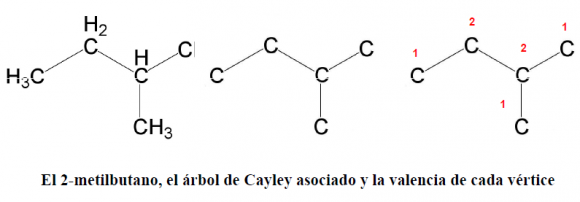
2. el 2-metilbutano –(CH3)2-CH-CH2-CH3– posee tres vértices de valencia 1 y dos de valencia 2; estos dos últimos son los centros:
Basándose en las propiedades de este tipo de árboles, Cayley propuso una fórmula para calcular el número de isómeros de los alcanos: su expresión era exacta para n de 1 a 11, pero fallaba más allá. También inventó un algoritmo que permitía calcular el número de isómeros para n conociendo el número de isómeros para n-1.
The Online Encyclopedia of Integer Sequences (OEIS) ofrece un amplio estudio sobre el número de isómeros de alcano, sin tener en cuenta los estereoisómeros –es decir, los isómeros que difieren sólo en la orientación espacial–. Cada isómero de alcano se identifica con un árbol sin raíz, de n vértices no etiquetados y de valencia menor o igual a 4 –como proponía Cayley, el no tener raíz significa que no hay vértices destacados–. Ignorar los estereoisómeros significa que las aristas que salen de un vértice no están ordenadas.
Además de incluir el número de alcanos hasta n=60, la OEIS incorpora fórmulas recurrentes para el cálculo de la cantidad de isómeros para cualquier valor de n. Incluso se distinguen los alcanos con un centro o con dos centros.
El número de isómeros de alcanos para n –es decir, C1H4 tiene 1 isómero, C2H6 tiene 1 isómero, C3H8 tiene 1 isómero, C4H10 tiene 2 isómeros, etc.– es:1, 1, 1, 2, 3, 5, 9, 18, 35, 75, 159, 355, 802, 1.858, 4.347, 10.359, 24.894, 60.523, 148.284, 366.319, 910.726, 2.278.658, 5.731.580, 14.490.245, 36.797.588, 93.839.412, 240.215.803, 617.105.614, 1.590.507.121, 4.111.846.763, 10.660.307.791, 27.711.253.769, etc.
Teniendo en cuenta estos cálculos, se estima que el alcano C167H336 posee más isómeros que partículas existen en el universo.
Para obtener el número completo de isómeros de alcano, basta con incorporar una ordenación a las aristas.
Referencias:
[1] P. Boulanger, Cayley et le calcul des isomères chimiques, Maths & Chimie, Tangente HS 43 (2012) 90-92
[2] E. M. Rains and N. J. A. Sloane, On Cayley’s Enumeration of Alkanes (or 4-Valent Trees), Journal of Integer Sequences, vol. 2 (1999) Article 99.1.1
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
Esta anotación participa en el XXXVIII Carnaval de la Química cuyo blog anfitrión es Pero eso es otra historia…

Chapu
En los isomeros del pantano ….el 2 metil butano para mi tiene 3 carbonos con Valencia 1 . Uno con 2 y otro con 3. No tres con 1 y dos con 2…además hablan de la fórmula q se cumple hasta C 11 pero no dicen cuál es