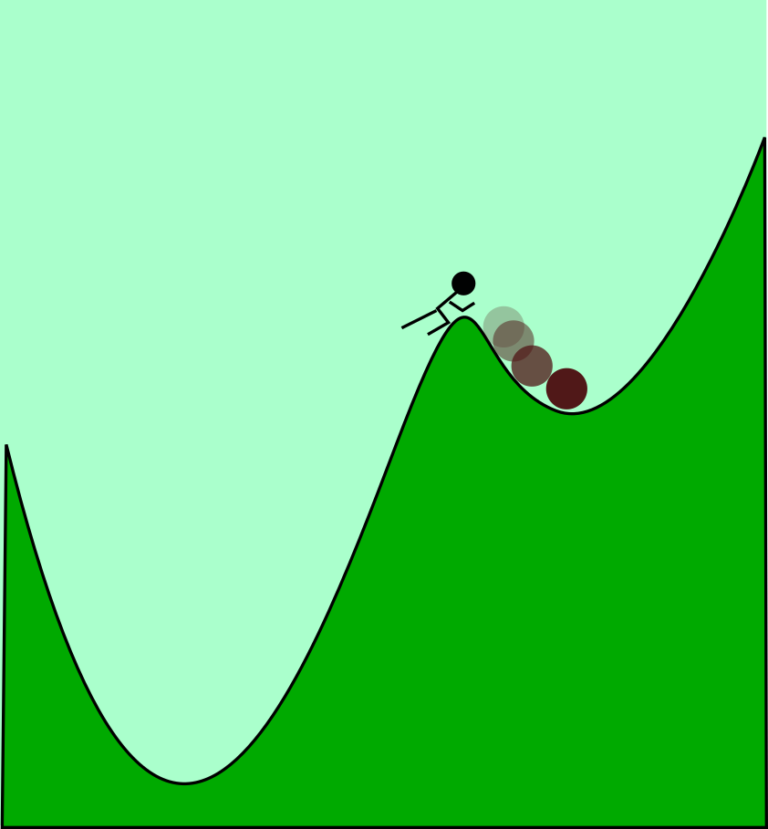
El sentido común, a pesar de su indudable utilidad, no siempre es la mejor guía hacia el conocimiento científico. Hay muchas verdades “de cajón” que nos explotan en los morros en cuanto tratamos de aplicarlas fuera de contexto. Hoy hablaré de una de ellas: la idea de que “siempre se puede desandar lo andado”.
Un buen ejemplo es la interesante reacción que tienen algunos niños tras caerse al suelo: se levantan rápidamente como diciendo “¡aquí no ha pasado nada!”. Pero claro que ha pasado algo; el trasero magullado sigue doliendo por muy rápido que uno se levante, y los raspones de las rodillas no se curan solos al recuperar la posición bípeda. Otros ejemplos serían un jarrón al romperse, un cocido con demasiada sal o un veraneante enrojecido por el exceso de insolación. Todas estas pequeñas desgracias cotidianas tienen algo en común: ha sucedido un proceso irreversible.
El concepto de irreversibilidad ocupa un papel central en la física estadística, y está muy relacionado con el escurridizo y a menudo mal entendido concepto de entropía. Sin embargo, no hablaré aquí de la irreversibilidad desde el complicado punto de vista de la física estadística, sino de otro concepto relacionado, una especie de irreversibilidad light, relacionada con el concepto de histéresis, mucho más asequible y cotidiano.
Imaginemos a Sísifo, aquel ser mitológico que debía empujar una piedra redondeada cuesta arriba, para dejarla caer de nuevo al llegar a la cima. Para poner las cosas un poco más interesantes, imaginemos que tiene que empujar la piedra por un paisaje como este:
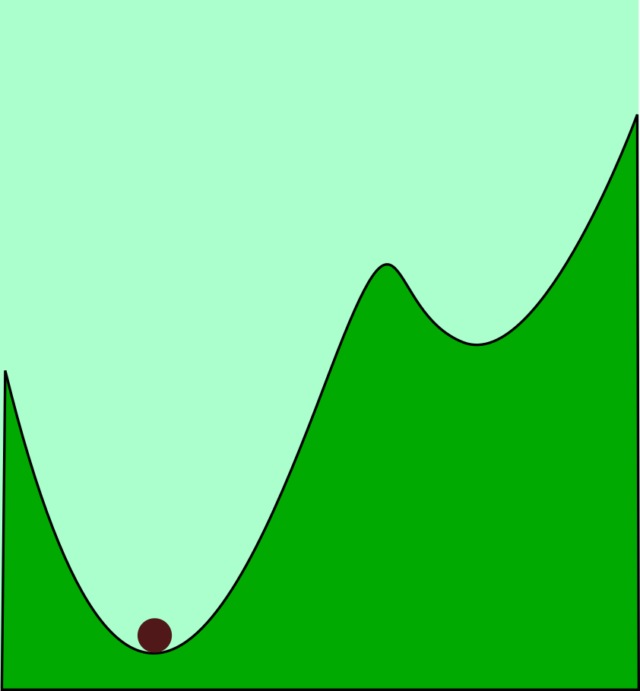
Si Sísifo quisiera colocar la piedra en el valle de la derecha, el más alto, tendría que empujarla como mínimo hasta el borde de la primera cresta, ¿verdad?
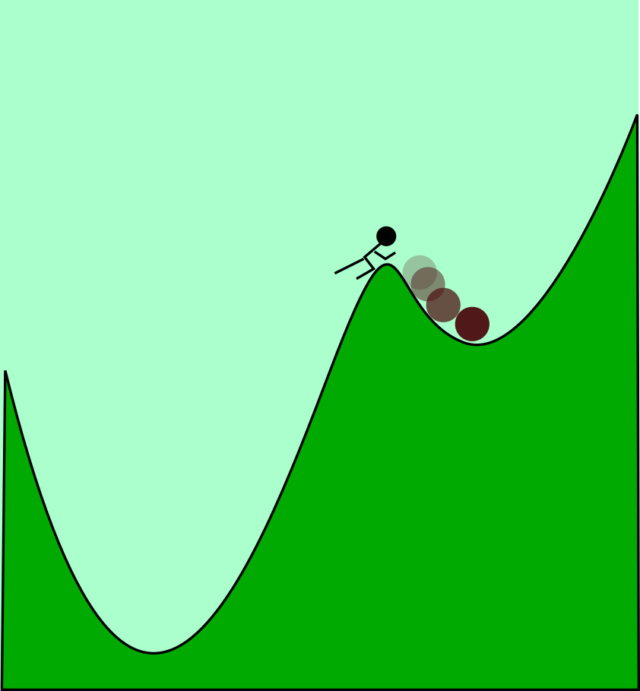
En el caso de que ahora Sísifo quisiera colocar la piedra una vez más en el valle izquierdo, el más profundo, tendría que volver a superar la cresta. Todo bastante evidente, ¿no?
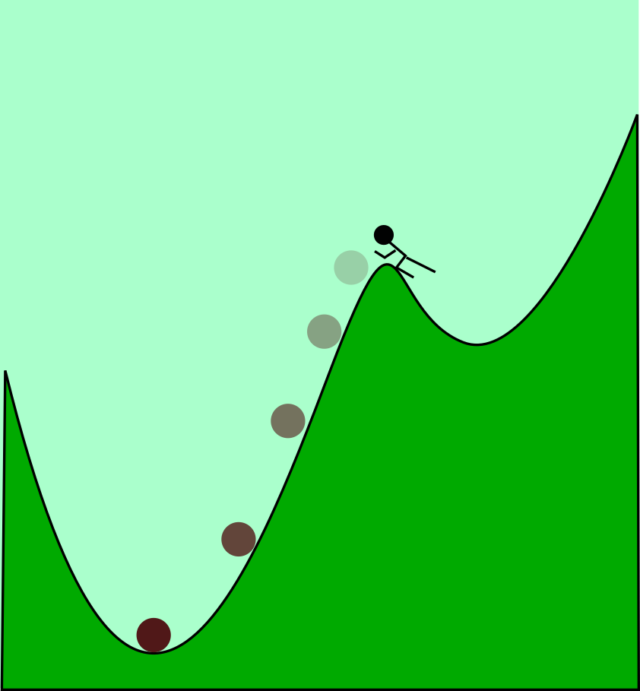
Lo interesante del caso es que, como el lector habrá observado, es mucho más fácil sacar la piedra de uno de los valles que del otro. Cuando la piedra se encuentra en el valle de la derecha, el más alto, basta un poco de esfuerzo para superar la primera cresta, y el relieve se ocupa de llevarse la piedra bien lejos, hasta el valle más profundo. El sistema no es irreversible en sentido estricto, pero el camino en un sentido es mucho más trabajoso que en el sentido opuesto.
Otra idea interesante y algo contraintuitiva que nos proporciona este ejemplo es la siguiente: cerca de la cresta, basta un pequeño empujón para desencadenar un gran movimiento.
Bonito ejemplo pero, ¿pueden aplicarse razonamientos análogos a problemas menos absurdos que el de un ser mitológico empujando una piedra? Lo cierto es que sí, pero tenemos que dar un paso atrás y mirar el problema de Sísifo con una perspectiva algo diferente: la de un sistema dinámico biestable. El problema imaginario de Sísifo es un sistema dinámico porque nuestro interés se concentra en el movimiento de la piedra, esto es, su posición en función del tiempo. Y es biestable porque la piedra puede quedarse quieta por sí sola en dos posiciones diferentes, los fondos de cada uno de los valles. De hecho, podemos interpretar la forma de nuestros montes y valles directamente como un mapa de potencial gravitatorio, convirtiendo nuestro ejemplo en un problema de mecánica:
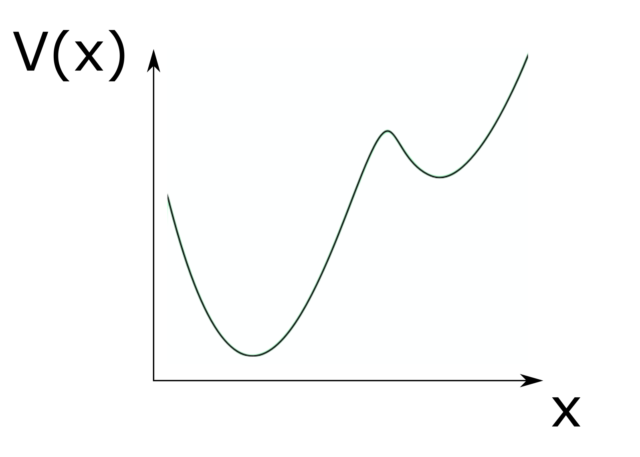
¿A dónde quiero llegar con todo esto?, pues a que no es difícil encontrar ejemplos de fenómenos naturales en los que, habiendo dos situaciones posibles, una de ellas es:
- Mucho más difícil de revertir que la otra.
- A partir de cierto umbral, el sistema evoluciona por sí solo hasta un estado alternativo.
El salto conceptual es menor de lo que pueda imaginarse, pues consiste en, simplemente, asignar magnitudes físicas a las alturas de nuestro paisaje montañoso. Existen importantes ejemplos como la histéresis magnética, los sistemas biestables en ecología o el modelo de superglaciación en clima (más conocido como Snowball Earth).
En el caso de la superglaciación podemos entender la altura de las “montañas” en nuestro gráfico como las posibles temperaturas medias del planeta, representando la posición de la piedra la temperatura concreta en un momento dado, y la posición de Sísifo empujando vendría dada por la concentración de gases de efecto invernadero[1]. La idea subyacente (y alarmante) es que si la concentración de gases alcanza cierto nivel crítico, las temperaturas podrían caer en picado sin necesidad de que “Sísifo siga empujando”, y no bastaría con retroceder a las concentraciones previas al desastre para recuperarse.
Una nota matemática:
Llegados a este punto, el lector familiarizado con las matemáticas y/o la física llevará un par de párrafos torciendo el gesto ante la presencia necesaria de Sísifo en todos los argumentos presentados. No me queda más remedio que darle la razón: en la mayoría de problemas físicos no hay lugar para un taumaturgo omnipotente que mueva a voluntad las condiciones iniciales del problema; si lo he usado en este artículo, ha sido en pro de la simplicidad.
Un análisis más certero del problema consiste en imaginar que la forma de las crestas y los valles de nuestro “potencial” dependen de cierto parámetro externo, al que llamaré S (sí, S de Sísifo) que, de algún modo, podemos controlar. La interpretación de dicho parámetro dependerá del problema en cuestión: puede ser una temperatura, un campo magnético externo o una concentración de gases de efecto invernadero.
Veamos un ejemplo gráfico en el que nuestro potencial se deforma tanto que la piedra cambia de sitio por sí sola:
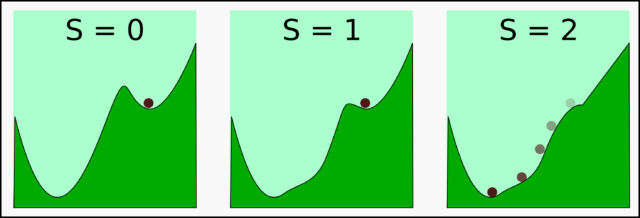
Lo interesante del caso, es que si ahora restituimos el valor de S a 0, recuperaremos la forma original, pero la piedra no volverá a su posición inicial:
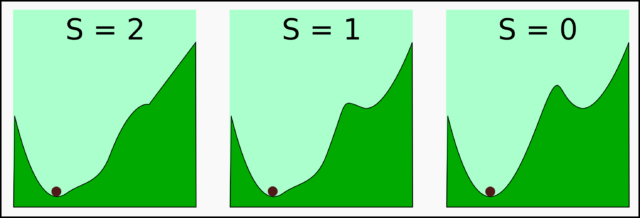
Quizá para valores negativos de S logremos deformar el paisaje lo suficiente como para revertir la situación, pero, una vez más, no habrá bastado con “desandar lo andado” (es decir, hacer S = 0).
Así se explica, por ejemplo (y a grandes rasgos), que ciertos materiales magnéticos puedan magnetizarse con ayuda del campo magnético generado y controlado por un electroimán (que sería nuestro Sísifo o parámetro externo) y que conserven su magnetización incluso cuando el electroimán vuelve a apagarse.
Existe toda una rama de las matemáticas, con el sugerente nombre de teoría de las catástrofes, dedicada a analizar y predecir este tipo de cambios bruscos en el comportamiento de un sistema.
Y es que, citando Ricky Martin, “un pasito p’alante y un pasito p’atrás”, pueden en ocasiones llevarte muy lejos.
Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
[1] En el modelo original, la concentración de gases de efecto invernadero afecta a la forma de “las montañas”, haciendo el ejemplo algo más complicado de entender. Ver apartado “Una nota matemática”.