En la asignatura de Matemáticas Básicas del primer curso del grado de matemáticas, uno de los ejercicios que hacemos en el tema de congruencias es el siguiente:

Ejercicio

Si

es la representación decimal de un entero positivo, probar que es divisible por 7 si y sólo si el número

también lo es.

La demostración se basa en las sencillas propiedades de teoría de congruencias; recordemos que dados tres enteros positivos m, n y d, se dice que m y n son congruentes módulo d, y se denota por

cuando m – n es divisible por d, o de otro modo, cuando el resto de la división de m y n por d es el mismo.

Teniendo en cuenta que:

y las propiedades de las congruencias, se deduce fácilmente el resultado anunciado. Así es como hacemos este ejercicio en el aula.

Aquí se presenta otro método –explicado en Blog de Maths– que permite averiguar si un número es divisible por 7, ¡sin necesidad de hacer ninguna operación!

Cuando acabes de leer esta entrada serás capaz de responder en medio minuto –o menos– a la pregunta ¿es 111.111.111 divisible por 7?,… y sin recurrir a la calculadora.

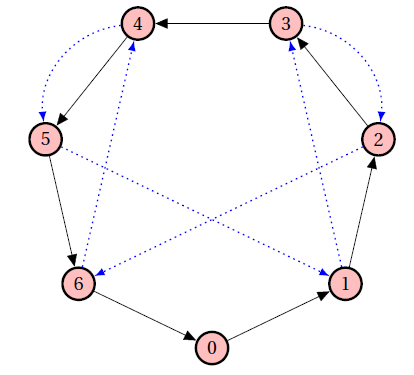
En Blog de Maths utilizan el siguiente grafo, en el que hay dos tipos de flechas: negras y azules, cada una de las cuales tiene un papel diferente que explicamos más adelante.

http://blogdemaths.wordpress.com

Vamos a dar un ejemplo de funcionamiento, y luego explicaremos la base matemática: comprobemos si 349 es divisible por 7 con ayuda del grafo.

Como no hemos regresado al vértice 0, se concluye que 349 no es divisible por 7.

En general, para ver si un número n es divisible por 7, hay que:

• partir del vértice 0,
• recorrer tantas flechas negras como la cifra situada más a la izquierda de n –en nuestro caso a_k– en la descomposición decimal de n,
• recorrer una flecha azul,
• recorrer tantas flechas negras como la cifra siguiente a_k-1,
• recorrer una flecha azul, etc.
• si al realizar esta operación con todas las cifras de la descomposición decimal de n llegamos al vértice 0, entonces n es divisible por 7 y no lo es en ningún otro caso.

Nota: si se cae en el vértice 0 antes de terminar, como no hay flecha azul se pasa directamente a la siguiente cifra.

¿Pero, por qué funciona esto?

• Las flechas negras representan la suma de una unidad módulo 7,
• y las flechas azules… bueno, para entender su utilidad, empecemos por el vértice 1, y vayamos recorriendo estas flechas; se va pasando por los números:

1, 3, 2, 6, 4, 5, 1,

que justamente son los restos de la división por 7 de 10⁰, 10¹, 10², 10³, 10⁴, 10⁵ y 10⁶–a partir de aquí, estos restos se van repitiendo de manera periódica–. Así, recorrer una flecha azul equivale a multiplicar el número del vértice sobre el que estamos por 10 módulo 7.

¿Por qué se empieza con la cifra situada más a la izquierda para n? ¿Por qué se recorre una flecha azul cada vez que cambiamos de cifra en la representación decimal de n?

Vamos a escribir el ejemplo estudiado, n = 349, de manera un poco diferente:

n = (3 x 10²) + (4 x 10¹) + (9 x 10⁰) = ((3 x 10) + 4) + 9.

Usando las propiedades de compatibilidad de la suma y el producto módulo 7 –las congruencias módulo 7 se conservan por sumas y productos–, empezamos por calcular 3 modulo 7 (recorremos tres flechas negras) y multiplicamos por 10 módulo 7 (recorremos una flecha azul), después sumamos 4 módulo 7 (recorremos cuatro flechas negras), después multiplicamos por 10 módulo 7 (recorremos una flecha azul), y finalmente sumamos 9 módulo 7 (recorremos nueve flechas negras). De hecho, el grafo nos proporciona en realidad el resto de la división de n por 7.

¿Es 111.111.111divisible por 7? El grafo te lo dirá… más aún, en tiempo récord te dirá que no, y que el resto es de hecho 6.

Fuente: Visto en Blog de Maths, en donde pueden verse también los grafos correspondientes a las divisiones por otros números enteros.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.