Una sextina es un poema formado por seis estrofas de seis versos cada una de ellas, que finaliza con una contera de tres versos. El trovador provenzal Arnaut Daniel fue el creador de esta forma poética; la primera sextina de la historia de la literatura es su Lo ferm voler qu’el cor m’intra:

Lo ferm voler qu’el cor m’intra

no’m pot ges becs escoissendre ni ongla

de lauzengier qui pert per mal dir s’arma;

e pus no l’aus batr’ab ram ni verja,

sivals a frau, lai on non aurai oncle,

jauzirai joi, en vergier o dins cambra.

Quan mi sove de la cambra

on a mon dan sai que nulhs om non intra

-ans me son tug plus que fraire ni oncle–

non ai membre no’m fremisca, neis l’ongla,

aissi cum fai l’enfas devant la verja:

tal paor ai no’l sia prop de l’arma.

Del cor li fos, non de l’arma,

e cossentis m’a celat dins sa cambra,

que plus mi nafra’l cor que colp de verja

qu’ar lo sieus sers lai ont ilh es non intra:

de lieis serai aisi cum carn e ongla

e non creirai castic d’amic ni d’oncle.

Anc la seror de mon oncle

non amei plus ni tan, per aquest’arma,

qu’aitan vezis cum es lo detz de l’ongla,

s’a lieis plagues, volgr’esser de sa cambra:

de me pot far l’amors qu’ins el cor m’intra

miels a son vol c’om fortz de frevol verja.

Pus floric la seca verja

ni de n’Adam foron nebot e oncle

tan fin’amors cum selha qu’el cor m’intra

non cug fos anc en cors no neis en arma:

on qu’eu estei, fors en plan o dins cambra,

mos cors no’s part de lieis tan cum ten l’ongla.

Aissi s’empren e s’enongla

mos cors en lieis cum l’escors’en la verja,

qu’ilh m’es de joi tors e palais e cambra;

e non am tan paren, fraire ni oncle,

qu’en Paradis n’aura doble joi m’arma,

si ja nulhs hom per ben amar lai intra.

Arnaut tramet son chantar d‘ongl’e d’oncle

a Grant Desiei, qui de sa verj’a l’arma,

son cledisat qu’apres dins cambra intra.

Sólo hay seis palabras que generan la rima –son 1=intra, 2=ongla, 3=arma, 4=verja, 5=oncle y 6=cambra en el poema de Arnaut Daniel– que van cambiando de lugar de acuerdo con el siguiente esquema:

123456 – 615243 – 364125 – 532614 – 451362 – 246531 – 531

En la sextina de Arnaut Daniel, aparecen las seis palabras en los tres versos finales, aunque no sucede siempre en estas composiciones poéticas. Observad que cada una de las seis palabras que riman pasan por todas las posiciones al cambiar de estrofa. El anterior esquema describe lo que en matemáticas se denomina una permutación –se alternan las seis palabras al cambiar de estrofa–; pero se trata además de una permutación de orden 6, es decir, cuando se hacen seis iteraciones –y no antes– se reencuentran las palabras de rima en su forma original. Si llamamos σ a esta permutación –e id a la ordenación natural (1, 2, 3, 4, 5, 6 )– se escribe del modo:

y es σ6=id, pero σ≠id, σ2≠id, σ3≠id, σ4≠id y σ5≠id.

En cada cambio de estrofa, la palabra que ocupaba el sexto lugar pasa a ocupar el primero, la que se situaba en el primero va a parar al segundo lugar, la que iba en el quinto puesto se traslada al tercero, la que ocupaba la segunda posición pasa a la cuarta, la que estaba en la cuarta va a parar a la quinta y, finalmente, la palabra situada en tercer lugar pasa a ocupar el sexto lugar de la estrofa.

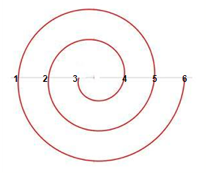
De otra manera, podemos pensar en los números del 1 al 6 colocados sobre una recta, y pensar σcomo una permutación en espiral que, además –como ya hemos comentado–, es una permutación de orden 6:

El escritor y cofundador del grupo OuLiPo Raymond Queneau [Jacques Roubaud, N-ine, autrement dit quenine (encore) en La bibliothèque oulipienne VI, Paris, Le Castor Astral, 2003] se preguntó si era posible generalizar la estructura de la sextina, reemplazando 6 por n, para escribir un poema de n estrofas, cada una formada por n versos, todos terminados por las mismas n palabras, intercambiadas por la permutación espiral:

La anterior permutación generaliza la estructura de las sextinas de Arnaut Daniel.

La pregunta ahora es la siguiente: ¿es posible generalizar las sextinas para cualquier valor de n? Dicho de otra manera, ¿la permutación espiralσdefinida por Queneau es siempre una permutación de orden n?

La respuesta es negativa: por ejemplo, para n=4, la permutación espiral definida por Queneau es σ(1)=2, σ(2)=4, σ(3)=3 y σ(4)=1. Pero σ es de orden 3, y no 4 como se desea (σ≠id, σ2≠id y σ3=id), al quedar el número 3 fijo por la permutación.

En honor a Queneau, las permutaciones espirales de orden n –las que permiten crear un poema generalizando a una sextina– se denominan queninas de orden n o n-ninas. Y se dice en tal caso que n es un número de Queneau.

No existen queninas de cualquier orden: acabamos de ver que no se dan para n=4. Tampoco existen 10-ninas: en este caso la permutación es de orden 7, no de orden 10.

Es posible caracterizar los números de Queneau en términos combinatorios. En [Jean-Guillaume Dumas, Caractérisation des quenines et leur représentation spirale, Mathematics and Social Sciences 184 (4), 9-23, 2008] se enuncia el siguiente teorema –cuyos términos se aclaran después–:

Teorema: Si n es un número de Queneau, entonces 2n+1 es un número primo. Además, si 2n+1 es primo, entonces existe una n-nina si y sólo si 2 es de orden 2n módulo 2n+1 o n es impar y 2 es de orden n módulo 2n+1.

La prueba es sencilla y preciosa… Pero aclaremos el enunciado :

1. Un número es primo si sólo es divisible por sí mismo y por 1.
2. 2 es de orden p módulo m si 2^p-1es divisible por m, pero 2^k-1noes divisible por m para k < p (estamos trabajando con enteros positivos).
3. Observad que cuando se dice en el enunciado «2 es de orden 2n módulo 2n+1 », n también puede ser impar.

Veamos unos ejemplos por si queda alguna duda:

1. n=1 es un número de Queneau, ya que 2n+1=3 es primo y 2²ⁿ–1 = 2²–1 = 3 es divisible por 3 (y 2^k–1 no es divisible por 3 para k < 2).
2. n=2 es un número de Queneau, ya que 2n+1=5 es primo y 2²ⁿ–1 = 2⁴–1 = 15 es divisible por 5 (y 2^k–1 no es divisible por 5 para k < 4).
3. n=3 es un número de Queneau, ya que 2n+1=7 es primo y 2ⁿ–1 = 2³–1 = 7 es divisible por 7 (y 2^k–1 no es divisible por 7 para k < 3). Fijaos que en este caso 2es de orden n módulo 2n+1(y no de orden 2n módulo 2n+1).
4. n=4 no es un número de Queneau, ya que 2n+1=9 que no es primo.
5. n=5 es un número de Queneau, ya que 2n+1=11 es primo y 2²ⁿ–1 = 2¹⁰–1 = 1023 es divisible por 11 (y 2^k–1 no es divisible por 11 para k < 10).
6. n=6 es un número de Queneau –¡las sextinas existen!–, ya que 2n+1=13 es primo y 2²ⁿ–1 = 2¹²–1 = 4095 es divisible por 13 (y 2^k–1 no es divisible por 13 para k < 12).
7. n=7 no es un número de Queneau, ya que 2n+1=15 no es primo.
8. n=8 no es un número de Queneau, ya que aunque 2n+1=17 es primo, el número 2⁸–1 = 255 es divisible por 17. El teorema dice que –si 8 fuera un número de Queneau– 2¹⁶–1 debería ser divisible por 17 (que lo es), pero 2^k–1 no debería ser divisible por 17 para k < 16.
9. n=9 es un número de Queneau, ya que 2n+1=19 es primo y 2²ⁿ–1 = 2¹⁸–1 = 262143 es divisible por 19 (y 2^k–1 no es divisible por 19 para k < 18).

10. n=10 no es un número de Queneau, ya que 2n+1=21 que no es primo.

¡Una auténtica belleza!

Los números de Queneau menores que 1000 son:

1, 2, 3, 5, 6, 9, 11, 14, 18, 23, 26, 29, 30, 33, 35, 39, 41, 50, 51, 53, 65, 69, 74, 81, 83, 86, 89, 90, 95, 98, 99, 105, 113, 119, 131, 134, 135, 146, 155, 158, 173, 174, 179, 183, 186, 189, 191, 194, 209, 210, 221, 230, 231, 233, 239, 243, 245, 251, 254, 261, 270, 273, 278, 281, 293, 299, 303, 306, 309, 323, 326, 329, 330, 338, 350, 354, 359, 371, 375, 378, 386, 393, 398, 410, 411, 413, 414, 419, 426, 429, 431, 438, 441, 443, 453, 470, 473, 483, 491, 495, 509, 515, 519, 530, 531, 543, 545, 554, 558, 561, 575, 585, 593, 606, 611, 614, 615, 618, 629, 638, 639, 641, 645, 650, 651, 653, 659, 683, 686, 690, 713, 719, 723, 725, 726, 741, 743, 746, 749, 755, 761, 765, 771, 774, 779, 783, 785, 791, 803, 809, 810, 818, 831, 833, 834, 846, 866, 870, 873, 879, 891, 893, 911, 923, 930, 933, 935, 938, 939, 950, 953, 965, 974, 975, 986, 989, 993, 998.

Se conjetura que existen infinitos números de Queneau… pero esa es otra historia.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.