Aunque ha habido algunas discusiones acerca de su definición, podemos decir que un fractal es un objeto irregular que presenta autosimilitudes a ciertas escalas. Ejemplos típicos de fractal son, por ejemplo, el Romanescu (en la naturaleza) o el conocido como conjunto de Mandelbrot:
Precisamente el propio Benoit B. Mandelbrot (1924- 2010) está considerado como el padre de la geometría fractal, rama de las matemáticas encargada del estudio de estos objetos. Y no es demasiado atrevido asegurar que la semilla a partir de la cual emergió este campo es el artículo de Mandelbrot How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension publicado en la revista Science en 1967. Lo que puede que no sepa todo el mundo es que la idea clave de este artículo proviene de un estudio anterior del matemático inglés Lewis Fry Richardson (1881-1953).
 Pero antes de comentar cuál fue esa idea vamos a ver qué tenía entre manos Lewis Richardson cuando llegó a ella. Además de matemático, Richardson era pacifista (y algunas cosas más), y en un momento de su vida se encontraba estudiando las causas de las guerras y cómo prevenirlas.
Pero antes de comentar cuál fue esa idea vamos a ver qué tenía entre manos Lewis Richardson cuando llegó a ella. Además de matemático, Richardson era pacifista (y algunas cosas más), y en un momento de su vida se encontraba estudiando las causas de las guerras y cómo prevenirlas.
En relación con esto pensó en estudiar cómo influía en que dos países entraran en guerra la longitud de frontera común que tuvieran, y recopilando datos sobre ello se encontró con cosas extrañas. Tan extrañas como que los datos de la longitud de ciertas fronteras variaban según la fuente que consultara. Y no variaban un poco, sino que lo hacían bastante, hasta en un 20% en algunos casos.
Estas variaciones no podían deberse al azar, tenían que estar producidas por algo. Y después de recoger una buena cantidad de datos Richardson llegó a la siguiente conclusión: la longitud de la frontera entre dos países depende de la unidad que se use para medir.
Es decir, si medimos la frontera común entre dos países con una regla que mida 20km obtendremos un resultado, pero si utilizamos una regla más pequeña, de, por ejemplo, 10km, el resultado obtenido será muy distinto, y además mayor.
Esto se puede apreciar en la imagen siguiente, en la que se mide la costa de Gran Bretaña con unidades de medida de 200km (izquierda), 100km (centro) y 50km (derecha):
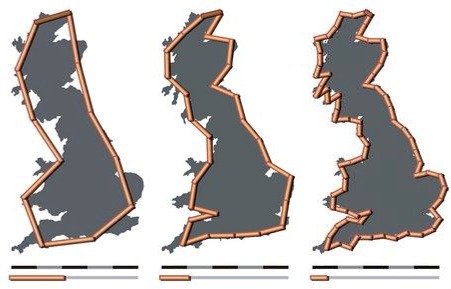 Los resultados que se obtienen de la longitud de dicha costa son, de izquierda a derecha, 2350km, 2775km y 3425km. Se aprecia aquí la sustancial diferencia en la longitud de esta costa para distintas unidades de medida.
Los resultados que se obtienen de la longitud de dicha costa son, de izquierda a derecha, 2350km, 2775km y 3425km. Se aprecia aquí la sustancial diferencia en la longitud de esta costa para distintas unidades de medida.
El caso es que no tendríamos por qué pararnos ahí, podríamos afinar más. Podríamos utilizar unidades de medida más pequeñas para obtener cada vez aproximaciones más precisas de la longitud de la frontera entre dos países, o de la longitud de una costa cualquiera, como la de Gran Bretaña. Se entiende que poco a poco nos iremos acercando al número finito que corresponderá con el valor real de esas longitudes, ¿no?
Pues no. Lo que Richardson obtuvo a partir de sus datos es que ese valor crece indefinidamente conforme vamos aumentado la escala. Es decir, que cuanto más afinamos con la unidad de medida mayor valor obtenemos para esas longitudes, y no podemos dejar de afinar. Vamos, que el límite (teórico) de estas aproximaciones sería infinito. Esto es lo que se conoce como efecto Richardson.
Por tanto, no podemos aspirar a encontrar la longitud concreta de la frontera común de dos países, o la longitud de la costa de Gran Bretaña, sencillamente porque no la hay. Si medimos esta costa desde un avión situado a 10km de altura obtendremos un valor para dicha longitud que (a escala) será menor que el obtenido si medimos desde el suelo paseando por la orilla del mar. Y éste valor será a su vez menor que el que se obtendría si utilizamos para medir un aparato del tamaño de una hormiga que vaya recorriendo la costa. Y así sucesivamente.
Para terminar, comentar que Lewis Fry Richardson también se dedicó a la Física y la Meteorología, siendo pionero en la utilización de técnicas matemáticas para la predicción del tiempo atmosférico. También da nombre al número de Richardson, que expresa la relación entre la energía potencial y la energía cinética de un fluido, y al método de extrapolación de Richardson, mediante el cual se puede mejorar el orden de convergencia de una sucesión.
Este artículo es una colaboración de la web Naukas.com con la Cátedra de Cultura Científica y su autor es @Gaussianos, uno de los más destacados divulgadores en el campo de las matemáticas.
Fuentes y más información:
Una nueva manera de ver el mundo, de Maria Isabel Binimelis.
Lewis Fry Richardson en Wikipedia

El efecto Richardson, la clave del estudio moderno de los fractales
[…] El efecto Richardson, la clave del estudio moderno de los fractales […]
fede cebrian
Echo en falta la conclusión del artículo, la cual para mí sería que, debido al efecto Richardson, el perímetro de cualquier cuerpo fractal es infinito.
Adalil Seguridad Alimentaria
Fascinante..
intergomas
He leído un libro titulado el fractal oculto y el enigma polar en donde aparecen las imágenes del mismo fractal, en el polo norte y sur de la tierra, en la luna y en Marte, el autor del libro le dio el nombre de fractal romboide cristal de luz. He seguido los pasos que dio el escritor y he visualizado ese fractal y fácilmente todos pueden hacerlo.
Como es posible que la ciencia no nos cuente sobre las repercusiones de esa formación fractal y lo que significa.
Es posible encontrar un fractal en la naturaleza con las características de fractales matemáticos? y por que aparece solo en los paralelos 90 grados de los cuerpos antes mencionados
theneowriter
¿Alguna bibliografía para aumentar todo esto? Me parece muy raro que conforme uno disminuya la longitud de la «regla» con la que mide, el resultado no converga a un valor… ¿No podría acotarse superiormente buscando alguna forma geométrica lo suficientemente grande?
Muy interesante, por lo demás.
lionel
No converge porque a medida que te acercas aparecen más y más detalles: una linea recta en el mapa podría ser una costa en forma de zig-zag, que a su vez tampoco está formada por líneas rectas ya que tiene pequeños salientes, que a su vez están formados por piedras, que tienen formas irregulares, bajo una lupa tienen poros, y al microscopio más de lo mismo, etc.
Pablo
Físicamente toda longitud de cualquier costa es finita, al utilizar como unidad de medida la longitud de Planck
El efecto Richardson, la clave del estudio moderno de los fractales | Informática Educativa y TICs | Scoop.it
[…] Aunque ha habido algunas discusiones acerca de su definición, podemos decir que un fractal es un objeto irregular que presenta autosimilitudes a ciertas escalas. Ejemplos típicos de fractal son, po… […]
El efecto Richardson, la clave del estudio moderno de los fractales | GESTIÓN TALENTO | Scoop.it
[…] Aunque ha habido algunas discusiones acerca de su definición, podemos decir que un fractal es un objeto irregular que presenta autosimilitudes a ciertas escalas. Ejemplos típicos de fractal son, po… […]
El efecto Richardson, la clave del estudio moderno de los fractales | matematicas y tecnologia | Scoop.it
[…] Aunque ha habido algunas discusiones acerca de su definición, podemos decir que un fractal es un objeto irregular que presenta autosimilitudes a ciertas escalas. Ejemplos típicos de fractal son, po… […]
CesarGon
También es interesante mencionar que, aunque el perímetro de un objeto fractal es infinito, la superficie que encierra es finita.
El efecto Richardson, la clave del estudio mode…
[…] Aunque ha habido algunas discusiones acerca de su definición, podemos decir que un fractal es un objeto irregular que presenta autosimilitudes a ciertas escalas. Ejemplos típicos de fractal son, po… […]
La forma fractal de mapas y pulmones — Cuaderno de Cultura Científica
[…] Como lo sería (figuradamente) el contorno de Gran Bretaña medido alrededor de cada grano de arena de su costa (o del peinado de Boris Johnson). El detalle de nuestra medida, la “escala” elegida, altera la medida misma. Esto es lo que se conoce como el efecto Richardson. […]