Según el Diccionario de la Real Academia Española la expresión Puente de los Asnos, Pons Asinorum, hace referencia a la “dificultad que se encuentra en una ciencia u otra cosa, y quita el ánimo para pasar adelante”, aunque esta expresión se suele utilizar generalmente para referirse a una prueba o test elemental de conocimiento, o de habilidad, que si no es superada demuestra la falta de capacitación en esa materia, y no se puede pasar el puente (“¿¡porque se es un burro!?”) para seguir adentrándose en el desarrollo de ese conocimiento o habilidad. Por poner algún ejemplo… interpretar al violín la “partita Nº 2 BWV 1004” de Johann Sebastian Bach si se quiere ser un gran violinista o podríamos decir que explicar el teorema de Pitágoras para quien va a ser profesor de matemáticas…

Hay quienes (en particular, parece que en Francia es así) utilizan esta expresión precisamente para referirse al Teorema de Pitágoras, puesto que sería un conocimiento elemental en geometría, que se habría utilizado desde la Edad Media como prueba para evaluar los conocimientos matemáticos de estudiantes, pero sobre todo de quienes se iban a dedicar a la docencia. Su relación con este resultado matemático quedó reflejada por ejemplo en el siguiente fragmento de la novela de Julio Verne, De la Tierra a la Luna:

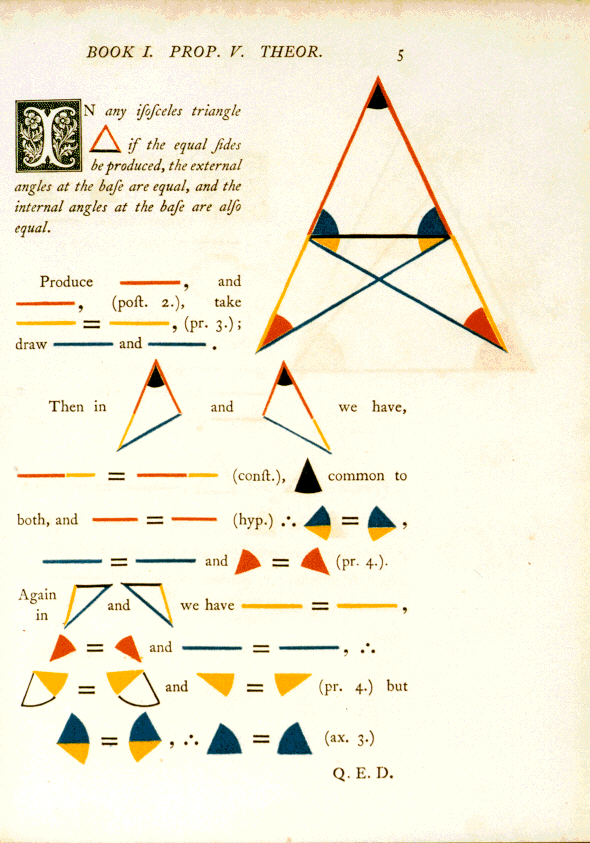
Sin embargo, la expresión Pons Asinorum o Puente de los Asnos no se refiere realmente al Teorema de Pitágoras, que es la Proposición 47 del libro Los Elementos de Euclides, sino a otra de sus proposiciones, la número 5, relacionada con los triángulos isósceles, que es de la que surge en realidad dicha expresión. En concreto, la Proposición 5 dice que: “los ángulos opuestos a los lados iguales de un triángulo isósceles, son también iguales”.

Según el filósofo griego Proclo (412-485), este resultado se debe a Tales de Mileto (s. VI a.n.e.), de cuya demostración solo conocemos lo comentado por el filósofo. Aunque no debía de ser la misma que se presenta en Los Elementos, ya que esta fue desarrollada por el propio Euclides, en opinión de muchos historiadores. Aristóteles (384-322 a.n.e.) y Pappus (290-350) también dieron otras demostraciones de ese resultado. Aunque, sin ninguna duda, la demostración más famosa y que dio lugar al término Pons Asinorum fue la que aparece en Los Elementos de Euclides.

Este resultado era conocido en las universidades de la Edad Media, como el Puente de los Asnos (en latín Pons Asinorum), ya que se consideraba que era el primer resultado avanzado en la enseñanza de las matemáticas y que marcaba un límite, a partir del cual no podían pasar ya los malos estudiantes. William Dunham, en su libro El universo de las matemáticas, dice que “Según la tradición, los ceporros –esto es, los burros- consideraban esta demostración insalvable, y por ello no podían cruzar el puente lógico y llegar a la tierra prometida de Los Elementos”. La proposición también se llamó “elefuga” (fuga miserorum), expresión que Roger Bacon (hacia 1250) explicó que significaba “el vuelo de los miserables”, porque era el punto en el que normalmente abandonaban la geometría. El nombre podría venir de que un triángulo isósceles se asemejaba a un puente (los antiguos puentes que estaban más elevados en el centro) y que a los burros, cuando iban con carga, les costaba pasar esos puentes, puesto que tenían que subir una pequeña inclinación.

Pero adentrémonos por un momento en las matemáticas del Pons Asinorum. Mostramos aquí precisamente la demostración de la Proposición 5 del Libro I de Los Elementos de Euclides, pero no la que aparece en el original, sino la que puede “disfrutarse” en la edición gráfica y coloreada (en diagramas tricolores, azul, rojo y amarillo, junto al negro) de Oliver Byrne de 1847. Toda una joya de las matemáticas, toda una obra de arte…

Y para terminar esta anotación en el Cuaderno, volvamos a la literatura. En la obra Trópico de Capricornio, de Henry Miller, puede encontrarse también una alusión al Pons Asinorum (y que descubrí en esta página):