Una contribución a la teoría matemática de la caza mayor
En 1938 se publicaba en la revista The American Mathematical Monthly el artículo [H. Pétard, A contribution to the mathematical theory of big game hunting, The American Mathematical Monthly, Vol. 45, no. 7 (Aug.-Sep., 1938), 446-447]… extraño título ¿verdad? ¿Una contribución a la teoría matemática de la caza mayor?
H. Pétard es un seudónimo tras el que se escondían los matemáticos Ralph P. Boas y Frank Smithies: al enviar el artículo al editor de la revista le solicitaron que no revelara sus nombres porque temían reacciones negativas de la comunidad científica.
En este artículo, Pétard describe una serie de procedimientos –basados en métodos matemáticos y de la física teórica y aplicada– que permitirían cazar un león en el desierto del Sahara, encerrándolo en una jaula.
De izquierda a derecha: Ralph Boas, Frank Smithies y Andre Weil
El artículo se introduce del siguiente modo[1]:
Esta poco conocida disciplina matemática no ha captado, estos últimos años, la atención en la literatura que, en nuestra opinión, se merece. En el presente artículo presentamos algunos algoritmos que esperamos sean de interés para otras personas que trabajen en este campo. Descartando los métodos triviales más obvios, centraremos nuestra atención en aquellos que impliquen aplicaciones significativas de ideas con las que matemáticos y físicos están familiarizados.
El momento actual es particularmente adecuado para la preparación de un informe sobre el tema, ya que los avances recientes en matemáticas puras y en física teórica han puesto a nuestra disposición poderosas herramientas cuya existencia era desconocida para los primeros investigadores. Además, algunos de los métodos clásicos más elegantes adquieren una nueva relevancia a la luz de los modernos descubrimientos. Como en muchas otras ramas del conocimiento en las que se han aplicado técnicas matemáticas en los últimos años, la Teoría Matemática de la Caza Mayor tiene un singular y afortunado efecto unificador sobre las más diversas áreas de las ciencias exactas.
Por simplificar la presentación, centraremos nuestra atención en leones (Felis leo) cuyo hábitat es el desierto del Sahara. Los métodos que enumeraremos son fácilmente aplicables, con las modificaciones formales obvias, a otros carnívoros y a otros lugares del planeta. El escrito está dividido en tres partes, cuyo material se extrae respectivamente de las matemáticas, la física teórica y la física experimental.
El autor quiere expresar su agradecimiento al Club de Trivial del St. John’s College, Cambridge, Inglaterra; a la sección de la Sociedad de Investigación Inútil del M.I.T.; al F. o. P. de la Universidad de Princeton; y a numerosos colaboradores individuales, conocidos o desconocidos, conscientes o inconscientes.
H. Pêtard, Princeton, New Jersey
Debajo se reproducen nueve –en total son dieciséis– métodos matemáticos propuestos por Pétard. Independientemente de la broma, las matemáticas aludidas son auténticas –y bellas–, y puede aprenderse –yo lo he hecho mientras lo leía y traducía– mucho de ellas.
1. EL MÉTODO AXIOMÁTICO O DE HILBERT. Ponemos una jaula cerrada en un punto dado del desierto. Introducimos entonces el siguiente sistema lógico.
AXIOMA I: El conjunto de los leones en el desierto del Sahara es no vacío.
AXIOMA II: Si hay un león en el desierto del Sahara, entonces hay un león en la jaula.
REGLA DE PROCEDIMIENTO: Si p es un teorema, y “p implica q” es un teorema, entonces q es un teorema.
TEOREMA I: Hay un león en la jaula.
2. EL MÉTODO DE LA GEOMETRÍA INVERSIVA. Situamos una jaula esférica en el desierto, entramos y la cerramos. Realizamos una inversión con respecto a la jaula. El león estará entonces dentro de la jaula, y nosotros fuera.
3. EL MÉTODO DE LA GEOMETRÍA PROYECTIVA. Sin pérdida de generalidad, podemos considerar que el desierto del Sahara es un plano. Proyectamos el plano en una recta, y después proyectamos la recta en un punto en el interior de la jaula. El león es así proyectado en ese mismo punto.
4. EL MÉTODO DE BOLZANO-WEIERSTRASS. Bisequemos el desierto mediante una recta que lo atraviese de norte a sur. El león está o bien en la parte este, o bien en la parte oeste; supongamos que está en la parte oeste. Bisequemos esta parte mediante una recta que vaya de oeste a este. El león está o bien en la parte norte o bien en la parte sur. Continuamos el proceso indefinidamente, construyendo una valla lo suficientemente resistente alrededor de la parte escogida en cada paso. El diámetro las partes elegidas tiende a cero, con lo que el león queda rodeado por una valla de perímetro arbitrariamente pequeño.
5. EL MÉTODO “MENGENTHEORETISCH”. Observamos que el desierto es un espacio separable[2]. Por lo tanto contiene un conjunto de puntos contable y denso, del cual podemos extraer una sucesión que tendrá al león como límite. Entonces nos aproximamos sigilosamente al león a lo largo de los términos de esta sucesión, llevando con nosotros el equipo adecuado.
6. EL MÉTODO DE PEANO. Construyamos, mediante procedimientos estándar, una curva continua que pase por cada punto del desierto. Como se ha observado[3] es posible atravesar esta curva en un intervalo de tiempo arbitrariamente pequeño. Equipados con una lanza, atravesamos la curva en un tiempo menor del que necesita el león para desplazarse una distancia equivalente a su propia longitud.
7. EL MÉTODO TOPOLÓGICO. Observamos que un león tiene al menos la conectividad del toro[4]. Podemos trasladar el desierto al espacio de cuatro dimensiones. Es entonces posible[5] realizar una deformación tal que el león puede regresar al espacio tridimensional en condición anudada. Entonces el león está indefenso.
8. EL MÉTODO DE CAUCHY O DE LA TEORÍA DE FUNCIONES. Consideremos la función analítica que toma valores en el conjunto de los leones f(z). Sea ζ la jaula. Consideremos la integral
donde C es la frontera del desierto; su valor es f(ζ), es decir, un león en la jaula.[6]
9. EL MÉTODO TAUBERIANO DE WIENER. Buscamos un león domesticado Lo, de clase L(-∞,∞), cuya transformada de Fourier no se anule en ningún punto, y liberémoslo en el desierto. Entonces Loconverge a nuestra jaula. Por el teorema general tauberiano de Wiener[7], cualquier otro león L deberá entonces converger a la misma jaula. De otra manera, podemos aproximarnos tanto como queramos a L trasladando Lo con respecto al desierto[8].
Nota: Aquí puede verse el artículo completo de Jstor. Desde su publicación, se han dado numerosas nuevas versiones de esta singular teoría matemática de la caza mayor. Muchas de ellas pueden encontrarse en[Lion hunting & other mathematical pursuits: A Collection of Mathematics, Verse, and Stories by Ralph P. Boas, Jr., The Dolciani Mathematuical Expositions Vol. 15, The Mathematical Association of America, 1995].
[1] Traducido del original por la autora.
[2] Nota de la autora: Un espacio se llama separable si existe un subconjunto que es denso y contable.
[3] Por Hilbert. Ver E.W. Hobson, The Theory of Functions of a Real Variable and the Theory of Fourier’s Series, 1927, vol. 1, pp. 456-457.
[4] Nota de la autora: se refiere a la superficie matemática llamada toro.
[5] H. Seifert and W. Threlfall, Lehrbuch der Topologie, 1934, pp. 2-3.
[6] Por el Teorema de Picard (W.F. Osgood, Lehrbuch der Funktionentheorie, vol. 1, 1928, p. 748), podemos cazar a todos los leones salvo a lo sumo uno.
[7] N. Wiener, The Fourier Integral and Certain of its Applications, 1933, pp. 73-74.
[8] N. Wiener, The Fourier Integral and Certain of its Applications, 1933, pp. 89.
Esta entrada participa en la edición 4.12310 del Carnaval de Matemáticas cuyo blog anfitrión es Geometría Dinámica.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

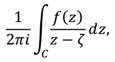
emulenews
Por cierto, recomiendo leer (en la misma línea): «Humor para matemáticos: 34 maneras de atrapar un león» http://francisthemulenews.wordpress.com/2011/08/03/humor-para-matematicos-34-maneras-de-atrapar-un-leon/
Una contribución a la teoría matemática de la caza mayor
[…] Una contribución a la teoría matemática de la caza mayor […]
Geometría Dinámica » Resumen del Carnaval de Matemáticas 4.12310
[…] Una contribución a la teoría matemática de la caza mayor (Cuaderno de Cultura científica) […]
Una contribución a la teoría matemática de la caza mayor |
[…] artículo Una contribución a la teoría matemática de la caza mayor de Marta Macho Stadler (Departamento de Matemáticas, ZTF-FCT) se publicó en el blog Cuaderno de […]